Критерий устойчивости Найквиста. Предназначен для анализа устойчивости замкнутых систем.

Предназначен для анализа устойчивости замкнутых систем.

Для случая, если разомкнутая цепь устойчива, условия устойчивости замкнутой САУ сводится к требованию, чтобы амплитудно-фазовая частотная характеристика (АФЧХ) разомкнутой цепи не охватывала точку (-1, j0).

Если АФЧХ разомкнутой цепи проходит через точку (-1, j0) , то можно записать

Но это возможно в том случае, если

то есть годограф Михайлова замкнутой САУ проходит через начало координат.

Таким образом, если АФЧХ разомкнутой цепи проходит через точку (-1, j0), то замкнутая САУ будет находится на границе устойчивости.

На рис.3.10 приведены две АФЧХ. Кривая 1 соответствует устойчивой САУ, кривая 2 - нахождению САУ на границе устойчивости.

Если, например, уменьшить коэффициент передачи в неустойчивой САУ, то ее АФЧХ будет сжиматься к началу координат, в результате чего система станет, наконец, устойчивой. Аналогично этому происходит и обратное.

Для САУ, имеющих неустойчивую разомкнутую цепь, условия устойчивости рассматривать не будем.

jQ

-1

0 Р

1 2

Рис.3.10

В соответствии с критерием Найквиста об устойчивости можно судить не только по АФЧХ, но и совместно по амплитудной и фазовой частотным характеристикам разомкнутой цепи. Обычно при этом пользуются логарифмическими характеристиками, что представляет большое удобство в силу простоты их построения. Но если ЛАЧХ используется асимптотическая, то расчеты будут достаточно грубыми.

Неохват АФЧХ точки (-1, j0) имеет место, если при частоте, на которой 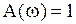, абсолютное значение фазы меньше p.

Но значение А=1 соответствует G=20lgA=0.

Поэтому для устойчивости замкнутой САУ необходимо, чтобы ЛАЧХ разомкнутой цепи пересекла ось абсцисс раньше, чем фаза, спадая, окончательно перейдет за значение - p.

На рис.3.11 приведены ЛАЧХ и ЛФЧХ, соответствующие устойчивости некоторой САУ.

G

0 lgw

-p

j

Рис.3.11

Критерий Найквиста позволяет оценить устойчивость САУ, содержащих звенья с запаздыванием.

Пусть звено с запаздыванием с передаточной функцией (при единичном коэффициенте передачи) включено последовательно с системой без запаздывания с передаточной функцией .

Результирующие передаточная и комплексная частотная функции разомкнутой цепи будут:

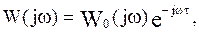
где

С учетом последнего

Видно, что звено с запаздыванием лишь вносит дополнительный сдвиг. При этом изменяется АФЧХ, т.е. меняются условия устойчивости (характеристика “закручивается” по часовой стрелке). При некотором t САУ станет неустойчивой.

По АФЧХ системы без запаздывания можно определить критическое (предельное) значение запаздывания 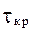, что поясняется построением на рис.3.12.

jQ

-1 p

Рис.3.12

Определяется точка, для которой Частота, соответствующая этой точке - 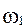, а фаза - .

При введении запаздывания условие совпадения этой точки с точкой (-1, j0) запишется

откуда

Физический смысл критерия Найквиста заключается в том, что при увеличении частоты входного воздействия сигнал, проходящий по цепи обратной связи, оказывается в противофазе с входным. А это равносильно замене отрицательной обратной связи на положительную. Если же при этой частоте разомкнутый контур обладает усилением (т.е. k>1), то замкнутая САУ становится неустойчивой (любое увеличение сигнала на выходе приводит к увеличению сигнала на входе по цепи обратной связи, что вызывает дальнейший рост выходного сигнала и т.д.).

Для аналитических расчетов с помощью критерия Найквиста условия нахождения системы на границе устойчивости можно записать в двух формах:

а) используя вещественную и мнимую частотные функции разомкнутой цепи

(3.8)

б) используя амплитудную и фазовую частотные характеристики разомкнутой цепи

(3.9)

Аналитические расчеты существенно упрощаются в частном случае, когда в числителе присутствует только коэффициент передачи k, как, например, в структуре на рис.3.3. При этом комплексную частотную функцию можно записать

=

где и - соответственно действительная и мнимая части знаменателя .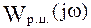

Но в том случае, если , значит

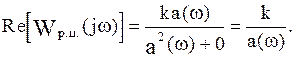
Тогда условия нахождения САУ на границе устойчивости (3.8) преобразуются к виду

или (3.10)

Определим, воспользовавшись условием (3.10), значение для структуры на рис.3.3.

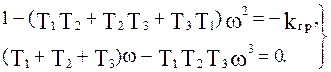
Из второго уравнения выразим (корень отбросим, т.к. по критерию Найквиста АФЧХ должна проходить через характерную точку при 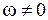) и подставим в первое уравнение:

Такой же результат был получен ранее по критериям Гурвица и Михайлова.