Кванттық механиканың негізгі ұстанымдарын заманауи тұрғыдан мысалдармен түсіндіріңіз.

Кванттық механика - атомдық деңгейдегі бөлшектердің қозғалысы мен

əсерлесулерінің жалпы заңдылықтарын зерттейді жəне осы заңдылықтарға сүйене отырып атом ядросының, атомның, молекулалар мен қатты денелердің құрылысы теориялары мен қасиеттерін тағайындайды.

Классикалық физиканың атомдардың қасиеттері мен құрылысын жəне олардың жарықпен əсерлесуін түсіндіре алмауына байланысты физиканың жаңа бөлігі–кванттық механика пайда болды.

Кванттық механика, физиканың басқа да бөліктері сияқты, нақты физикалық құбылыстарды математикалық кескіндер (өрнектер, қатынастар) түрінде сипаттайды. Бұл кескіндер негізгі математикалық объектілерден: функциялардан, матрицалардан, операторлардан жəне олардың арасындағы қатынастардан құралады. Осы математикалық образдар мен физикалық объектілер – электрондар, атомдар жəне молекулалар арасындағы сəйкестік негізгі физикалық ұғымдар арқылы тағайындалады. Бір жағынан, бұл физикалық ұғымдар математикалық заңдылықтар мен əдістерді пайдалануға болатын математикалық объектілермен сипатталуы қажет, ал екінші жағынан, физикалық кұбылыстың мазмұны осы физикалық үғымдар арқылы сипатталатын физикалық құбылыстар мен тəжірибелерді қарастыру нəтижесінде тағайындалады.

Кванттық механика қазіргі заманғы физиканың негізгі теориясының бірі. Кванттық механика - микробөлшектердің (элементар бөлшектердің, атомдардың, молекулалардың) қозғалыс заңдылықтарын зерттейтін теория.

Кванттық механиканың алғашқы даму тарихын қарастыра отырып, негізгі үш кезеңді ерекше бөліп алуға болады. Бірінші кезең: XIX ғасырдың аяғы - 1912 ж. (алғашқы тәжірибелер және оларды түсіндіру әрекеттері). Екінші кезең: 1913 - 1922 ж.ж. (Бордың кванттық теориясы). Үшінші кезең: 1923 - 1927 ж. ж. (кванттық механиканың пайда болуы және дамуы).

XIX ғасырдың аяғында және XX ғасырдың басында рентгендік сәулелер, электрондар, спектрлер, радиоактивті құбылыс және т.б. физикалық құбылыстар ашылды. Осыған байланысты ғалымдар микрообьектілерді зерттеуге мүмкіндік алды. Алғашқы кванттық ұғымды енгізген неміс физигі М.Планк. 1900 жылы 14 желтоқсанда Планк «Қалыпты спектрдегі энергияның үлестірілу теориясына» деген еңбегін Немістің физикалық қоғамының мәжілісінде баяндады. Осы күнді кванттық теорияның туған күні деп есептеуге болады. Классикалық сәулелену теориясы бойынша жарық үзіліссіз түрде шығарылады. Бұл ұғым бойынша физиктер абсолют қара дененің сәулеленуінің эксперименттік қисығын түсіндіре алмады. Осы қиыншылықты жою үшін Планк, жарық үзікті түрде, яғниатомдар энергияны жеке порциялармен шығарады деп болжаған. Энергияның бір мөлшерін ол латынның квант (қанша) деген сөзімен атады. Планк гипотезасын(ғылыми болжамын)пайдалана отырып неміс ғалымы А. Эйнштейн 1905 жылы фотоэффект құбылысын және 1907 жылы қатты денелердің жылу сыйымдылығының температураға тәуелділігін түсіндірді. 1911 жылы ағылшын физигі

Э. Резерфорд - бөлшектердің ауыр элементтер атомдарымен соқтығысуын зерттей отырып, атомның планетарлық моделін ұсынды.

Кванттық механиканың пайда болуына дейін микрообъектілерде болатын физикалық құбылыстарды классикалық физиканың (Ньютон механикасы, классикалық электрдинамика және т.б.) көмегімен түсіндіру әрекеттері болды. Бірақ эксперименттік берілгендер классикалық физиканың заңдылықтары кеңістіктің микроскопиялық аймағында орындалмайтындығын көрсетті. Мысалы, атомдар Ньютон заңдарына бағынбайды. Классикалық физика атомдардың электрмагниттік сәулеленуімен өзара әрекетін, мыстың не себепті өткізгіш, ал шынының - оқшаулағыш болатынын түсіндіре алмады. Себебі, классикалық физика заттың микроқұрылысы рөл атқармайтын құбылыстарды қарастырады. Сонымен, ХХ ғасырдың басында классикалық физика түсіндіре алмайтын эксперименттік фактілер көптеп жинақталды. Оларды тек кванттық теорияның көмегімен түсіндіруге болды.

Кванттық механиканың негіздерін құруда классикалық физикада қолданылатын бірсыпыра көрнекі және үйреншікті ұғымдардан бас тартуға тура келді. Мысалы, классикалық механикада материялық нүкте траектория бойынша қозғалса, кванттық механикада бөлшек траекториясы ұғымы жоқ. Классикалық физикада барлық объектілер энергияны үзіліссіз түрде шығарса, кванттық теория бойынша атомның сәуле шығаруы үзікті сипатта болады. Классикалық физикада заңдар динамикалық сипатта болса, кванттық заңдар статистикалық сипатқа ие болады.

Кванттық механиканың осы жаңа ұғымдары көрнекілік қасиеттерге ие болмайды. Микрообъектілердің қасиеттерін түсіндіру үшін мүлде басқаша теория қажет болды және соған сәйкесті жаңа математикалық аппарат қолдану керек болды.

Кванттық физика атомдар, ядролар және элементар бөлшектер физикасын, яғни кванттық құбылыстарды зерттейді. Осы кванттық құбылыстардың қазіргі заманғы математикалық теориясы кванттық механика деп аталады. Кванттық механика, қарастырылатын бөлшектердің жылдамдықтарына байланысты екі түрге бөлінеді: релятивистік емес кванттық механика (бұл жағдайда бөлшектер жылдамдығы жарық жылдамдығы 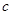- дан өте кіші, ) және релятивтік кванттық механика ( ).

Кванттық механиканың көмегімен көптеген физикалық құбылыстарды түсіндіруге болады. Оны негізге ала отырып, атомдық спектрлердің, молекулалар құрылысының, элементтердің периодтық жүйесінің, металдың өткізгіштік, химиялық байланыс және т.б. теориялары жасалды. Осы сияқты өрістің кванттық теориясы да біз қарастыратын кванттық механикаға негізделген.

Классикалық механикада Ньютонның теңдеуі және электродинамикада Максвелл теңдеулері қандай рөл атқарса, кванттық механикада Шредингер теңдеуінің рөлі сондай болады. Ньютон және Максвелл теңдеулері сияқты, Шредингер теңдеуі қорытылмайды. Шредингер теңдеуі постулат түрінде қабылданады, яғни белгілі тәжірибелердің қорытындысы болып саналады.

Бірақ, Шредингер теңдеуін себептілік принципінің көмегімен формальды түрде алуға болады. Бұл әдістің тарихи және әдіснамалық маңызы бар. Себептілік принципі бойынша бастапқы уақыттағы толқындық функция кейінгі уақыттағы толқындық функциямен байланысты болады. Осы байланысты қалай табуға болады? Оны табу үшін функцияны 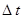уақыт мезетінде қарастырайық, яғни

-ді қатарға жіктейміз:

Себептілік принципі бойынша 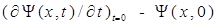функциядан анықталу керек:

мұндағы - ны алу үшін 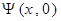- ге қатысты жасалатын амал. Біздің жағдайда кез келген түрде алынған, сондықтан

,

мұндағы - уақыт бойынша ығысу операторы.

Кванттық механикадағы анықтама бойынша, оператор - бір толқындық функцияны басқа толқындық функцияға ауыстыратын кез келген математикалық символ. Сондықтан теңдеудегі оператор постулат түрінде қабылдану керек. Суперпозиция принципі бойынша сызықтық түрде болу керек. Бұл операторда уақыт бойынша алынған туындылар мен интегралдар болмау керек, ал тек параметр ретінде болу керек. Егер керісінше жорамалдасақ, онда функция жүйе күйін сипаттайды деген кванттық механиканың негізгі қағидасы бұзылады. Бұл теңдеудің көмегімен бастапқы функция арқылы функциясын табуға болады, осыған сәйкес уақыттағы әр түрлі өлшеулер нәтижелерінің ықтималдығын болжауға болады. Сонымен және теңдеулерді салыстыра отырып, еркін қозғалысқа арналған уақыт бойынша ығысу операторын табамыз:

.

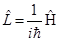Кванттық механикада бұл нәтижені жалпы түрде жазуға болады, ол үшін ығысу операторын Гамильтон функциясының операторы ретінде қарастыру керек

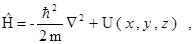
мұндағы -бөлшектің потенциалдық энергиясы. Сонымен постулатқа сәйкес теңдеуді мына түрде жазуға болады:

.

Бұл теңдеуді 1926 жылы басқа әдіспен Шредингер алған, ол Шредингер теңдеуі немесе Шредингердің толқындық теңдеуі деп аталынады. Шредингер теңдеуінің ерекшелігі, ол уақыт бойынша бірінші ретті теңдеу және оның құрамына комплекс бірлік кіреді, сол себепті оның периодты шешімдері болады. Сондықтан да, Шредингер теңдеуі толқындық теңдеу болады.

Резерфорд ұсынған планетарлық моделі бойынша, ядроны айнала қозғалатын электрон үзіліссіз энергия бөліп шығара отырып, белгілі бір уақыттан кейін ядроға құлауы керек. Бірақ бұл тұжырым атомның электрлік бейтарап жəне орнықты жүйе екендігіне қайшы келеді. Осы қайшылықты жою үшін Бор (1913 ж.) атомның классикалық планеталық моделін төмендегідей екі постулатпен толықтырды.

1 постулат: Əрбір атом дискретті стационар күйлерге ие, бұл күйлердегі электрондар үдей қозғалғанмен де, энергия бөліп шығармайды. Бор теориясы бойынша, бұл стационар күйлер адиабатты инварианттарды h -Планк тұрақтысын кванттау арқылы анықталады.

2 постулат: Электрон энергиясы , n E n кванттық күйден, энергиясы E n n ¢ - ¢ квант- тық күйге n n E ¢ < E ауысқанда атом энергиясы тең сəуле бөліп шығарады жəне бұл сəулелердің жиілігі мынадай қатынас бойынша анықталады. Бор постулаттарының дұрыстығы 1913 ж. Франк-Герц тəжірибесінің негізінде тағайындалды. Атом күйлерінің дискретті екендігі Франк-Герц (1913 ж.) тəжірибелерінде дəлелденді.