Основные теоремы преобразования Лапласа

1. Теорема линейности

Если функции и являются оригиналами, изображения которых и F₂(s) соответственно, и если величины с₁ и с₂ не зависят от t и s, то справедливо равенство

2. Теорема дифференцирования

Пусть

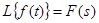, f(0) – начальное значение функции

тогда

Если начальные условия нулевые, то

Таким образом, дифференцированию оригиналов отвечает умножение изображений на s. Это свойство позволяет сводить решение линейных дифференциальных уравнений с постоянными коэффициентами в области оригиналов к решению алгебраических уравнений в области изображений.

3. Теорема интегрирования

Если функция f(t) является оригиналом и F(s) — его изображение, то для н.н.у. справедливо равенство:

т. е. интегрированию в области оригиналов соответствует деление изображения на s.

4. Теорема запаздывания

Если функция f(t) является оригиналом и F(s) — его изображение, то изображение смещенного оригинала , где τ > 0, определяется равенством:

.