Передаточная функция. Операторное уравнение и структурная схема звена.

С преобразованием Лапласа связано понятие передаточной функции звена (или системы), играющее важную роль в теории линейных систем.

Рассмотрим для простоты дифференциальные уравнения 2-ого порядка – модель некоторого звена

.

Будем считать, что начальные условия нулевые, то есть до подачи входного сигнала система находилась в статическом режиме (отклонение переменных от номинальных значений равны нулю).

Преобразуем по Лапласу обе части уравнения, то есть перейдем от оригиналов к изображениям.

Применяя теорему линейности получим

.

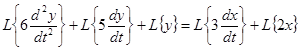Используем теорему дифференцирования при нулевых начальных условиях в результате получим

.

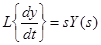
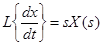
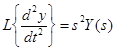Уравнение с учетом последних формул принимает вид

.

Вынесем X(s) и Y(s) за скобки, тогда

.

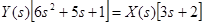Выразим Y(s) и получим операторное уравнение звена

.

Для дифференциального уравнения n-ого порядка

операторное уравнение находится аналогично и имеет вид

или

,

где - передаточная функция системы

Передаточная функция системы — отношение изображений по Лапласу выходного сигнала Y(s) к входному X(s) при нулевых начальных условиях.

Передаточная функция является эквивалентом ДУ. Зная W(s) и X(s) легко определить Y(s), а затем и решение ДУ y(t) (оригинал), если начальные условия нулевые.

При ненулевых начальных условиях операторное уравнение имеет вид

,

где Y_н(s) определяется начальными условиями.

Отметим некоторые свойства передаточной функции

1. Формально W(s) – эквивалент дифференциального уравнения (другая форма записи)

Числитель образуется из коэффициентов b_i правой части ДУ, а знаменатель из коэффициентов левой a_i заменой k-ой производной на s^k

2. Знаменатель W(s) есть характеристический полином D(s), то есть

.

3. Коэффициент усиления определяется по формуле

Формулу легко получить, записав уравнение статики звена.

Звено с несколькими входами характеризуется несколькими передаточными функциями

которые определяются в соответствии с принципом суперпозиции.

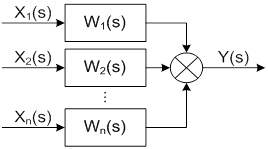
Операторное уравнение имеет вид

Операторному уравнению можно поставить в соответствии структурную схему