Характеристики замкнутой АСР

В данном разделе мы получим операторное уравнение и передаточные функции замкнутой АСР. Структурная схема АСР приведена на рисунке

На схема пунктирной линией выделен объект управления. Для простоты считаем, что действует одно возмущение.

На схеме обозначены:

W_р(s) – передаточная функция регулятора,

W_у(s), W_в(s) – передаточные функции объекта по каналу управления и возмущения,

X(s), E(s), U(s), F(s), Y(s) – изображения по Лапласу сигналов задания, ошибки, управления, возмущения, регулируемой величины.

Операторное уравнение объекта

.

Введем в рассмотрение понятие разомкнутой системы. Для чего разорвем обратную связь и примем F=0. Поскольку регулятор и объект включены последовательно то справедлива формула

.

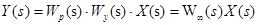Выражение

называется передаточной функцией разомкнутой системы.

Найдет теперь характеристики замкнутой АСР. Входными сигналами АСР являются задание X(s) и возмущение F(s) выходным – регулируемая величина Y(s) (или ошибка E(s)), то есть замкнутая АСР характеризуется двумя передаточными функциями: по задающему Ф_З(s) и по возмущающему воздействию Ф_В(s). Операторное уравнение в силу принципа суперпозиции (наложения) можно записать следующим образом

Для определения Ф_З(s) и Ф_В(s) воспользуемся принципом суперпозиции. При F(s)=0 структурная схема представляет собой соединение с обратной связью.

Тогда

,

где - последовательное соединение

W_ОС=1 – стопроцентная обратная связь.

Тогда

.

Проложим теперь X=0, найдем Ф_В(s).

Входом является F(s), выходом – Y(s). Свернутая схема

,

где Ф_экв(s) – эквивалентная передаточная функция обратной связи.

Передаточная функция

.

Таким образом

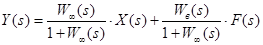или

,

где ,

,

.

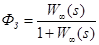Уравнение статики

,

где ,

.

Найдем уравнение замкнутой АСР относительно ошибки

.

Приведя подобные члены, получим операторное уравнение замкнутой системы относительно ошибки

,

где .

Уравнение статики

,

где .

Знаменатели всех трех передаточных функций Ф_З(s), Ф_В(s), Ф_Е(s) совпадают – это характеристический полином замкнутой АСР. Получим для него формулу.

Пусть ,

где – характеристический полином разомкнутой системы.

Тогда

.

Таким образом, характеристический полином замкнутой системы можно определить как сумму полинома числителя и знаменателя передаточной функции разомкнутой АСР

.