Тема 3. Магнитное поле в веществе

Все вещества, помещенные в магнитное поле, намагничиваются. Рассмотрим причину этого явления с точки зрения строения атомов и молекул. Мы говорили, что существуют макротоки и микротоки.

Микротоки обусловлены движением электронов в атомах и молекулах. Электрон в атоме движется по круговым орбитам, поэтому он обладает орбитальным магнитным моментом p_m = IS = evS

где I = ev – сила тока

n - частота вращения электрона по орбите, S – площадь орбиты

p_m Если электрон движется по часовой стрелке,

I то ток направлен против часовой стрелки и

r e вектор p_m по правилу правого винта перпен-

дикулярен плоскости орбиты электрона.

u С другой стороны, движущийся по орбите

L_e электрон обладает механическим моментом

импульса L_e

L_e = mur = 2mnS – орбитальный момент электрона

где u = 2pn r S = p r²

Направление момента импульса L_e также подчиняется правилу правого винта.

Направления вектора магнитного момента p_m и механического момента импульса L_e противоположны, поэтому

- гиромагнитное отношение орбитальных моментов.

«-» показывает, что вектор магнитного момента p_m и механического момента импульса L_e противоположны.

Электрон также обладает собственным механическим моментом импульса L_eS – спином. Спин является неотъемлемым свойством электрона, подобно его заряду и массе. Спину электрона L_eS соответствует собственный (спиновый) магнитный момент

р_mS = q_SL_eS

g_S – гиромагнитное отношение спиновых моментов.

Проекция р_mS на направление вектора магнитной индукции В

где h - постоянная Планка;

m_В – магнетон Бора – единица магнитного момента электрона.

Тогда общий магнитный момент атома (молекулы)

равен сумме орбитальных и спиновых магнитных моментов, входящих в атом электронов. Таким образом, атомы обладают магнитными моментами.

Всякое вещество является магнетиком, т.е. способно под действием поля намагничиваться или приобретать магнитный момент. По своим магнитным свойствам магнетики подразделяются на три основные группы: диамагнетики, парамагнетики и ферромагнетики.

Всякое вещество при внесении её во внешнее магнитное поле намагничивается в той или иной степени, т.е. создает свое собственное магнитное поле, накладывающееся на внешнее поле.

Количественной характеристикой намагниченного состояния вещества служит векторная величина – намагниченность j, равная отношению магнитного момента малого объема вещества к этому объему DV.

p_mi – магнитный момент i-го атома из общего числа n атомов, содержащихся в объеме DV. Этот объем DV должен быть столь малым, чтобы в его пределах магнитное поле можно считать однородным.

Диамагнетики – вещества, которые намагничиваются во внешнем магнитном поле в направлении, противоположном направлению вектора магнитной индукции В и ослабляют магнитное поле. В отсутствии внешнего поля магнитный момент p_m=0 и m<1. При внесении диамагнетика в магнитное поле атомы приобретают наведенные магнитные моменты, пропорциональные вектору магнитной индукции В и противоположны ему по направлению.

Парамагнетики - вещества, которые намагничиваются во внешнем магнитном поле в направлении вектора магнитной индукции В. Атомы (молекулы или ионы) парамагнетика обладают собственным магнитным моментом р_m – намагничивается, усиливает магнитное поле m>1. Процесс намагничивания парамагнетиков состоит в упорядочении расположения магнитных моментов его атомов (молекул) по отношению к направлению вектор магнитной индукции В.

Ферромагнетики – сильномагнитные вещества, обладающие спонтанной намагниченностью, т.е. намагничены даже при отсутствии внешнего поля.

j Для диа- и парамагнетиков зависи-

j_нас ферро мость j от Н линейна, то для ферро-

магнетиков по мере возрастания

пара напряженности Н намагниченость

j растет вначале быстро, а потом

Н медленнее и наступает магнитное

насыщение j_нас, уже не зависящее

диа от напряженности поля.

j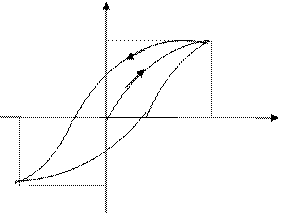

Если намагнитить ферромагнетик до

j_нас 1 насыщения (точка 1), а затем начать

2 уменьшать напряженность намагни-

6 чивающего поля, то уменьшение на-

-Н_нас -Н_с 0 Н_е Н магниченности описывается кривой

3 Н_нас 1-2. При Н = 0, намагниченность не

-j_ост 5 равна нулю, т.е. наблюдается ос-

таточная намагниченность j_ост.

4 -j_нас

магнитный гистерезис

В постоянных магнитах намагниченность j обращается в нуль под действием поля Н_с, имеющего направление, противоположное полю, вызывающему намагничивание. Напряженность Н_с называется коэрцитивной силой. При дальнейшем увеличении противоположного поля ферромагнетик перемагничивается (3-4) и при Н = -Н_нас достигается насыщение (точка 4). Затем ферромагнетик можно опять размагнитить (4-5-6) и вновь перемагнитить до насыщения (6-1). Ферромагнетики обладают еще одной особенностью - для каждого ферромагнетика имеется определенная температура, при которой он теряет свои особые магнитные свойства – точка Кюри. Эти свойства ферромагнетиков объясняется особенностью их структуры – доменной структурой. В ферромагнетике имеются небольшие области – домены, которые представляют собой маленькие магнитики, внутри которых магнитные моменты всех молекул направлены в одну сторону. Так, как расположение самих доменов беспорядочно, то суммарный магнитный момент большого куска намагниченного ферромагнетика равен нулю. Когда ферромагнетик помещают в магнитное поле, происходит ориентировка магнитных моментов доменов и в результате возникает макроскопическое намагничение.

Циркуляцией вектора магнитной индукции В в вакууме по замкнутому контуру называется интеграл

где dl – вектор элементарной длины контура, направленной вдоль обхода контура

B_l = Bcosα – составляющая вектора В в направлении касательной к контуру

α – угол между векторами В и dl.

Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора В)

n – число проводников с током, охватываемых контуром.

В веществе на магнитное поле макротоков В₀ (называется внешним) накладывается дополнительное магнитное поле микротоков (внутреннее) - В_внут.

Таким образом, магнитная индукция В зависит от магнитных свойств магнетика.

В общем случае

Тогда, можно записать

В = В₀ + В_внут

Магнитная индукция В характеризует результирующее магнитное поле в веществе

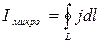Для поля в веществе

Тогда закон полного тока для магнитного поля в веществе

- напряженность магнитного поля

Тогда - закон полного тока для магнитного поля в среде

или теорема о циркуляции напряженности Н.

С помощью закона полного тока можно вычислить магнитное поле соленоида и тороида.

Соленоид – цилиндрическая катушка с током, состоящая из большого числа витков проволоки, которые образуют винтовую линию.

- магнитная индукция поля внутри соленоида

N - число витков; - число витков на единицу длины.

Тороид - кольцевая катушка с током, витки которой намотаны на сердечник, имеющий форму тора.

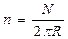
В этом случае , где ℓ = 2πR – длина окружности

Тогда - магнитная индукция поля тороида.