
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определители второго и третьего порядков
Рассмотрим систему двух линейных уравнений с двумя неизвестными:
 (1)
(1)
Умножая обе части первого уравнения на  , а второго на
, а второго на  и затем складывая уравнения, получим
и затем складывая уравнения, получим 
Умножая первое уравнение на –а2, а второе на а1 и после этого складывая уравнения, получим 
Из этих уравнений при условии  получим решение системы (1).
получим решение системы (1).

 (2)
(2)
Заметим, что знаменатели в формулах (2) составлены из коэффициентов  ,
,  ,
,  ,
,  при неизвестных системы (1). Условились записывать число
при неизвестных системы (1). Условились записывать число  в виде таблицы
в виде таблицы 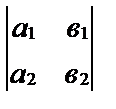 и назвали его определителем второго порядка, т.е.
и назвали его определителем второго порядка, т.е.
 =
=  .
.
Аналогично,
 =
=  и
и  =
=  .
.
Формулы (2) теперь можно записать с помощью трех определителей второго порядка, составленных из коэффициентов при неизвестных и свободных членов системы (1): 
 , где
, где
 =
=  - определитель системы,
- определитель системы,
 =
=  - определитель неизвестного х,
- определитель неизвестного х,
 =
=  - определитель неизвестного у.
- определитель неизвестного у.
 Формулы (2) позволяют сформулировать правило Крамера для решения системы (1).
Формулы (2) позволяют сформулировать правило Крамера для решения системы (1).
Если определитель  системы не равен нулю, то система имеет единственное решение. Это решение находится по формулам:
системы не равен нулю, то система имеет единственное решение. Это решение находится по формулам:
 ,
,  .
.
Вернемся к определителю второго порядка  =
=  .
.
Определитель второго порядка – это число, вычисленное по таблице, составленной из четырех чисел (элементов)  ,
,  ,
,  ,
,  . Элементы определителя расположены в двух строках (
. Элементы определителя расположены в двух строках (  и
и  в первой строке,
в первой строке,  и
и  во второй строке) и в двух столбцах (
во второй строке) и в двух столбцах (  и
и  в первом столбце,
в первом столбце,  и
и  во втором столбце).
во втором столбце).
Диагональ, на которой расположены элементы  ,
,  называется главной, диагональ из элементов
называется главной, диагональ из элементов  ,
,  называется побочной. Таким образом, определитель
называется побочной. Таким образом, определитель  равен разности произведений элементов, стоящих соответственно на главной и побочной диагоналях.
равен разности произведений элементов, стоящих соответственно на главной и побочной диагоналях.
Если для системы (1) определитель системы  =
=  , то
, то  =
=  получается из
получается из  заменой первого столбца (т.е. коэффициентов при х) столбцом свободных членов,
заменой первого столбца (т.е. коэффициентов при х) столбцом свободных членов,  =
=  получается из
получается из  заменой второго столбца (из коэффициентов при у) столбцом свободных членов.
заменой второго столбца (из коэффициентов при у) столбцом свободных членов.
Примеры.
№1. Решить систему

 ;
;


№ 2 Решить систему 


№ 3 Решить систему 
Запишем систему в определенном порядке:  .
.

Рассмотрим систему трех линейных уравнений с тремя неизвестными. Удобнее все неизвестные обозначить буквой х с индексом (х1, х2, х3), все коэффициенты при неизвестных – одной буквой а с двумя индексами, из которых первый – номер уравнения, второй – номер неизвестного.
 (3)
(3)
Определитель, составленный из коэффициентов при неизвестных (он содержит девять элементов, записанных в три строки и в три столбца), назовем определителем системы (3).
 - определитель третьего порядка.
- определитель третьего порядка.
Укажем правило Сарруса для вычисления определителя третьего порядка:

Для удобства покажем схему, по которой вычисляют определитель третьего порядка.

| · · · | + | · · · | + | · · · | – | · · · | – | · · · | · · · | |
| · · · | · · · | · · · | · · · | · · · | - | · · · | ||||
| · · · | · · · | · · · | · · · | · · · | · · · |
Итак, произведения элементов, соединенные пунктиром, входят в сумму со знаком плюс или со знаком минус.
Примеры.
№ 4. 

Для системы трех линейных уравнений с тремя неизвестными правило Крамера формулируется аналогично уже доказанному.
Если определитель  системы не равен нулю, то система имеет единственное решение, которое находится по формулам:
системы не равен нулю, то система имеет единственное решение, которое находится по формулам:

Здесь 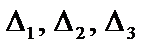 - определители при неизвестных
- определители при неизвестных  соответственно, полученные из определителя
соответственно, полученные из определителя  системы заменой столбца коэффициентов при соответствующей неизвестной столбцом из свободных членов.
системы заменой столбца коэффициентов при соответствующей неизвестной столбцом из свободных членов.
№ 5. 

Проверкой убедимся, что решение системы найдено правильно:
2×2-5+3=2 верно
5×2-5+3×3=14 верно
2×2-5+2×3=5 верно
Ответ: х=2, у= –5, z=3.
Дата добавления: 2015-01-05; просмотров: 280; Мы поможем в написании вашей работы!; Нарушение авторских прав |