
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Матричный способ решения системы линейных уравнений
Обратимся вновь к системе п линейных уравнений с п неизвестными.
 (4)
(4)
Покажем, что эту систему можно записать в виде одного матричного уравнения. Для этого введем в рассмотрение матрицы:
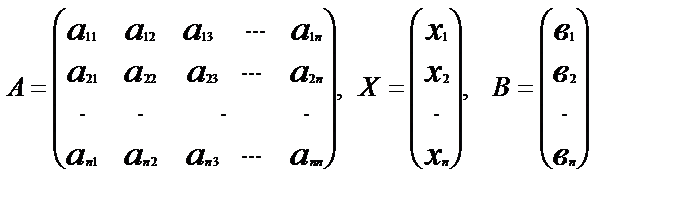 .
.
Назовем А – матрицей системы, Х – столбцом неизвестных, В – столбцом свободных членов. Рассмотрим уравнение А×Х=В.
Умножая первую строку матрицы А на столбец Х, получим первый элемент  матрицы В, т.е.
матрицы В, т.е.

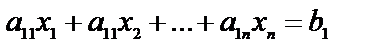 .
.
А это и есть первое уравнение системы (4). Аналогично, получим и все остальные уравнения системы (4).
Итак, система (4) может быть представлена одним уравнением
А×Х=В, (5)
которое и является матричной формой системы (4).
Если матрица А системы (4) невырожденная, то существует матрица А-1, обратная для матрицы А. Умножим слева обе части уравнения (5) на А-1. Получим А-1×А×Х=А-1×В. Так как А-1×А=Е и Е×Х=Х, то имеем
Х=А-1×В (6)
Формула (6) дает матричную запись решения системы (4).
Рассмотрим пример
№ 14. Решить систему матричным способом

Запишем систему в определенном порядке

 ,
,
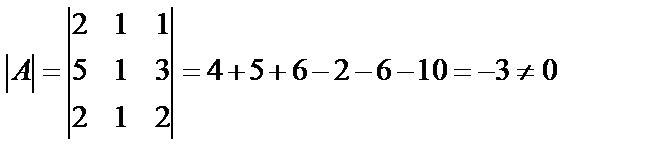 т.е. матрица А – невырожденная. Найдем обратную матрицу А-1.
т.е. матрица А – невырожденная. Найдем обратную матрицу А-1.

 - обратная матрица.
- обратная матрица.
Решение системы найдем по формуле (6):

Решение системы: х=2; у= –5; z=3. Подстановкой в систему легко проверить правильность решения.
Таким образом, крамеровскую систему можно решить по формулам Крамера или матричным способом.
Дата добавления: 2015-01-05; просмотров: 315; Мы поможем в написании вашей работы!; Нарушение авторских прав |