
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алексей Викторович Иванов 7 страница
Определить расстояние между точками А(3;8) и В(-5;14).
$$ 10
Определить угол между векторами:  и
и  .
.
$$ 135°
Определить угловой коэффициент К прямой  .
.
$$0
Определить уравнение прямой проходящей через две точки  и
и  :
:
$$ 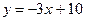
ППП
Первые три члена ряда  есть числа:
есть числа:
$$ 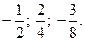
Повторный интеграл, к которому сводится  , где
, где  , равен:
, равен:
$$ 
Повторный интеграл, к которому сводится  , где
, где  , равен:
, равен:
$$ 
Порядок дифференциального уравнения  равен:
равен:
$$ 1.
Порядок дифференциального уравнения  равен:
равен:
$$3
Порядок дифференциального уравнения  равен:
равен:
$$5
Порядок дифференциального уравнения  равен:
равен:
$$ 5
Порядок дифференциального уравнения  равен:
равен:
$$ 4
Предел слева в точке разрыва функции  равен:
равен:
$$ 0
При каких значениях параметров а и в матрица  имеет обратную матрицу?
имеет обратную матрицу?
$$ a  1, b
1, b  1
1
При каком значении С плоскости 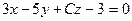 и
и  перпендикулярны?
перпендикулярны?
$$6
При каком значении В прямая  проходит через точку (2;-1)?
проходит через точку (2;-1)?
$$-1
Проекция на оси абсцисс координат направленного отрезка, или вектора  на плоскости с началом
на плоскости с началом 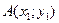 и концом
и концом  , определяется:
, определяется:
$$ 
Проекция на оси ординат координат направленного отрезка, или вектора  на плоскости с началом
на плоскости с началом 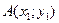 и концом
и концом  , определяется:
, определяется:
$$ 
Производная функции  равна
равна
$$ 
Производная функции  , есть функция:
, есть функция:
$$ 
Производная функции  есть:
есть:
$$  .
.
Производная функции  , есть функция вида:
, есть функция вида:
$$ 
Производная функции 
$$ 
Пусть  . Тогда производная функции
. Тогда производная функции  равна:
равна:
$$ 
Пусть  . Тогда производная функции
. Тогда производная функции  равна:
равна:
$$ 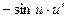
РРР
Разложение дроби 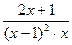 на сумму простых дробей имеет вид:
на сумму простых дробей имеет вид:
$$ 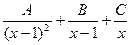 .
.
Разложение дроби  на сумму простых дробей имеет вид:
на сумму простых дробей имеет вид:
$$ 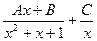 .
.
Ранг матрицы системы уравнений  равен:
равен:
$$ 2.
Ранг расширенной матрицы для системы уравнений  равен:
равен:
$$ 3
Расстояние  между точками
между точками  и
и  на плоскости:
на плоскости:
$$ 
Расстояние от точки  до плоскости
до плоскости 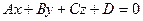 определяется:
определяется:
$$ 
Решением системы уравнений  является множество:
является множество:
$$ 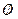 .
.
Решить дифференциальное уравнение первого порядка  .
.
$$  Решение системы уравнений:
Решение системы уравнений: 
$$ (-8;4;3).
Решите систему уравнений 
$$ 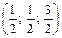
Решите уравнение:  :
:
$$ 
Решите уравнение  .
.
$$ 
Решите уравнение:  .
.
$$  .
.
Решите уравнение:  .
.
$$  .
.
Решите уравнение  :
:
$$ 
Решите уравнение:  :
:
$$ 
Решите уравнение:  :
:
$$ 
Решите уравнение:  .
.
$$ 
Решите уравнение: 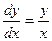 .
.
$$ 
Решите уравнение: 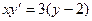 :
:
$$ 
Решите уравнение 
$$ 
Решить уравнение  .
.
$$ 
Решить уравнение  .
.
$$ -1
Решить уравнение  , удовлетворяющее условию
, удовлетворяющее условию  .
.
$$ 
Решить уравнение: 
$$ 
Решить уравнение 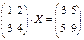 .
.
$$ 
Решить уравнение: 
$$ 
ССС
Середина отрезка находится в точке М(1;4), один из концов в точке А(-2;2).
Определить координаты отрезка другого конца.
$$ (4;6)
Система линейных алгебраических уравнений называется совместной, если
$$ имеет только одно решение
Случайная величина Х задана интегральной функцией распределения:

Найти математической ожидание М(Х).
$$ 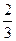 .
.
Смешанное произведение векторов  равно:
равно:
$$ 0
Смешанное произведение векторов  равно
равно
$$ 1
Среди рядов:  (1),
(1),  (2),
(2), 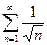 (3) укажите сходящие ряды:
(3) укажите сходящие ряды:
$$ 2.
Составить уравнение плоскости, которая проходит через точку А(2;1;-1) и имеет нормальный вектор  .
.
$$ 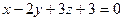
Составить уравнение плоскости, проходящей через начало координат перпендикулярно вектору  , если А(5;-2;3) и В(1;-3;5).
, если А(5;-2;3) и В(1;-3;5).
$$ 
Составить уравнение плоскости, проходящей через точку М(2;-2;0) перпендикулярно вектору  .
.
$$ 
Составить уравнение прямой, зная ее угловой коэффициент  и отрезок
и отрезок  , отсекаемый ею на оси ОУ.
, отсекаемый ею на оси ОУ.
$$ 
Составить уравнение прямой, проходящий через 0(0;0) и точку А(2;-1).
$$ 
Составить уравнение прямой, проходящей через точку А(3;-1) и параллельной прямой  .
.
$$ 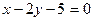
Составить уравнение прямой, проходящей через точку А(3;-1) и перпендикулярной прямой  .
.
$$ 
Сумма 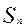 первых
первых  членов числового ряда
членов числового ряда 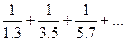
$$ 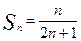
ТТТ
Точка максимума функции  имеет координаты:
имеет координаты:
$$ (-1;5)
Точка минимума функции  , есть точка с координатами
, есть точка с координатами
$$ 
УУУ
Укажите количество точек максимума функции  :
:
$$ 0
Укажите количество точек экстремума функции  :
:
$$0
Укажите общее решение линейного однородного уравнения, соответствующего уравнению  :
:
$$ 
Укажите общий член ряда: 
$$ 
Уравнение  является дифференциальным уравнением:
является дифференциальным уравнением:
$$ линейным относительно неизвестной функции.
Уравнение  является дифференциальным уравнением:
является дифференциальным уравнением:
$$ в полных дифференциалах
Уравнение плоскости в отрезках имеет вид:
$$ 
Уравнение плоскости, проходящей через точку  и перпендикулярным вектору
и перпендикулярным вектору  имеет вид.
имеет вид.
$$ 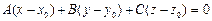
Уравнение прямой в отрезках имеет вид:
$$ 
Уравнение прямой с угловым коэффициентом имеет вид:
$$ 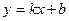
Уравнение прямой, проходящей через точки А(0; 2; 3), В(1; 0; 1), есть
$$ 
Уравнение прямой, проходящей через точки  , есть:
, есть:
$$  .
.
Уравнение прямой, проходящей через точку М(-2; 0) перпендикулярно прямой  , имеет вид
, имеет вид
$$ 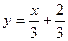
Уравнение пучка прямых, проходящих через данную точку
$$ 
ФФФ
Фокус параболы  находится в точке
находится в точке
$$ 
Фокус параболы  , находится в точке:
, находится в точке:
$$ 
Фокус параболы  находится в точке:
находится в точке:
$$ 
Фокусы гиперболы  находятся в точках
находятся в точках
$$  .
.
Фокусы гиперболы с полуосями и действительной осью ОХ есть точки (точка) с координатами:
$$  .
.
Фокусы эллипса  находятся в точках:
находятся в точках:
$$ (1;0);(-1;0)
Фокусы эллипса с данными полуосями 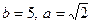 находятся в точках:
находятся в точках:
$$ 
ХХХ
Характеристическое уравнение однородного линейного дифференциального уравнения с постоянными коэффициентами  имеет вид:
имеет вид:
$$  .
.
Характеристическое уравнение однородного линейного дифференциального уравнения с постоянными коэффициентами  имеет вид:
имеет вид:
$$ 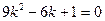
Характеристическое уравнение однородного линейного дифференциального уравнения с постоянными коэффициентами  имеет вид:
имеет вид:
$$ 
Характеристическое уравнение однородного линейного дифференциального уравнения с постоянными коэффициентами  имеет вид:
имеет вид:
$$  .
.
Характеристическое уравнение дифференциального уравнения  имеет вид:
имеет вид:
$$ 
ЧЧЧ
Чтобы понизить порядок дифференциального уравнения  необходимо использовать замену:
необходимо использовать замену:
$$ 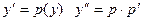
Чтобы привести интеграл  к табличному интегралу, надо применить замену:
к табличному интегралу, надо применить замену:
$$  .
.
Чтобы привести интеграл  к табличному интегралу, надо применить замену:
к табличному интегралу, надо применить замену:
$$ 
Чтобы решить уравнение  надо применить метод:
надо применить метод:
$$ разделить переменные
ЭЭЭ
Эксцентриситет кривой  равен:
равен:
$$ 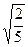 .
.
Эксцентриситет кривой  равен:
равен:
$$ 
Эксцентриситет кривой 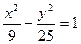 равен:
равен:
$$  .
.
Эксцентриситет эллипса  равен:
равен:
$$  .
.
Алексей Викторович Иванов
Дата добавления: 2015-01-05; просмотров: 261; Мы поможем в написании вашей работы!; Нарушение авторских прав |