
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алексей Викторович Иванов 4 страница
$$ 
Решить уравнение: 
$$ 
ССС
Середина отрезка находится в точке М(1;4), один из концов в точке А(-2;2).
Определить координаты отрезка другого конца.
$$ (4;6)
Система линейных алгебраических уравнений называется совместной, если
$$ имеет только одно решение
Случайная величина Х задана интегральной функцией распределения:

Найти математической ожидание М(Х).
$$ 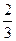 .
.
Смешанное произведение векторов  равно:
равно:
$$ 0
Смешанное произведение векторов  равно
равно
$$ 1
Среди рядов:  (1),
(1),  (2),
(2), 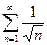 (3) укажите сходящие ряды:
(3) укажите сходящие ряды:
$$ 2.
Составить уравнение плоскости, которая проходит через точку А(2;1;-1) и имеет нормальный вектор  .
.
$$ 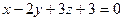
Составить уравнение плоскости, проходящей через начало координат перпендикулярно вектору  , если А(5;-2;3) и В(1;-3;5).
, если А(5;-2;3) и В(1;-3;5).
$$ 
Составить уравнение плоскости, проходящей через точку М(2;-2;0) перпендикулярно вектору  .
.
$$ 
Составить уравнение прямой, зная ее угловой коэффициент  и отрезок
и отрезок  , отсекаемый ею на оси ОУ.
, отсекаемый ею на оси ОУ.
$$ 
Составить уравнение прямой, проходящий через 0(0;0) и точку А(2;-1).
$$ 
Составить уравнение прямой, проходящей через точку А(3;-1) и параллельной прямой  .
.
$$ 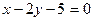
Составить уравнение прямой, проходящей через точку А(3;-1) и перпендикулярной прямой  .
.
$$ 
Сумма 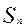 первых
первых  членов числового ряда
членов числового ряда 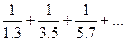
$$ 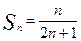
ТТТ
Точка максимума функции  имеет координаты:
имеет координаты:
$$ (-1;5)
Точка минимума функции  , есть точка с координатами
, есть точка с координатами
$$ 
УУУ
Укажите количество точек максимума функции  :
:
$$ 0
Укажите количество точек экстремума функции  :
:
$$0
Укажите общее решение линейного однородного уравнения, соответствующего уравнению  :
:
$$ 
Укажите общий член ряда: 
$$ 
Уравнение  является дифференциальным уравнением:
является дифференциальным уравнением:
$$ линейным относительно неизвестной функции.
Уравнение  является дифференциальным уравнением:
является дифференциальным уравнением:
$$ в полных дифференциалах
Уравнение плоскости в отрезках имеет вид:
$$ 
Уравнение плоскости, проходящей через точку  и перпендикулярным вектору
и перпендикулярным вектору  имеет вид.
имеет вид.
$$ 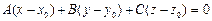
Уравнение прямой в отрезках имеет вид:
$$ 
Уравнение прямой с угловым коэффициентом имеет вид:
$$ 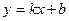
Уравнение прямой, проходящей через точки А(0; 2; 3), В(1; 0; 1), есть
$$ 
Уравнение прямой, проходящей через точки  , есть:
, есть:
$$  .
.
Уравнение прямой, проходящей через точку М(-2; 0) перпендикулярно прямой  , имеет вид
, имеет вид
$$ 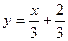
Уравнение пучка прямых, проходящих через данную точку
$$ 
ФФФ
Фокус параболы  находится в точке
находится в точке
$$ 
Фокус параболы  , находится в точке:
, находится в точке:
$$ 
Фокус параболы  находится в точке:
находится в точке:
$$ 
Фокусы гиперболы  находятся в точках
находятся в точках
$$  .
.
Фокусы гиперболы с полуосями и действительной осью ОХ есть точки (точка) с координатами:
$$  .
.
Фокусы эллипса  находятся в точках:
находятся в точках:
$$ (1;0);(-1;0)
Фокусы эллипса с данными полуосями 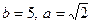 находятся в точках:
находятся в точках:
$$ 
ХХХ
Характеристическое уравнение однородного линейного дифференциального уравнения с постоянными коэффициентами  имеет вид:
имеет вид:
$$  .
.
Характеристическое уравнение однородного линейного дифференциального уравнения с постоянными коэффициентами  имеет вид:
имеет вид:
$$ 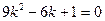
Характеристическое уравнение однородного линейного дифференциального уравнения с постоянными коэффициентами  имеет вид:
имеет вид:
$$ 
Характеристическое уравнение однородного линейного дифференциального уравнения с постоянными коэффициентами  имеет вид:
имеет вид:
$$  .
.
Характеристическое уравнение дифференциального уравнения  имеет вид:
имеет вид:
$$ 
ЧЧЧ
Чтобы понизить порядок дифференциального уравнения  необходимо использовать замену:
необходимо использовать замену:
$$ 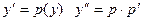
Чтобы привести интеграл  к табличному интегралу, надо применить замену:
к табличному интегралу, надо применить замену:
$$  .
.
Чтобы привести интеграл  к табличному интегралу, надо применить замену:
к табличному интегралу, надо применить замену:
$$ 
Чтобы решить уравнение  надо применить метод:
надо применить метод:
$$ разделить переменные
ЭЭЭ
Эксцентриситет кривой  равен:
равен:
$$ 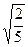 .
.
Эксцентриситет кривой  равен:
равен:
$$ 
Эксцентриситет кривой 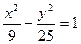 равен:
равен:
$$  .
.
Эксцентриситет эллипса  равен:
равен:
$$  .
.
ААА
Абсцисса середины отрезка  , где
, где  равна:
равна:
$$ 
Аппликата вектора  , если даны точки А(5; 2; 3), В(1; 2; -1), равна:
, если даны точки А(5; 2; 3), В(1; 2; -1), равна:
$$ 4.
ВВВ
В выражении 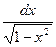 внести функцию под знак дифференциала:
внести функцию под знак дифференциала:
$$ 
В выражении  ввести функцию под знак дифференциала
ввести функцию под знак дифференциала
$$ 
В интеграле  ,чтобы применить формулу интегрирования по частям
,чтобы применить формулу интегрирования по частям 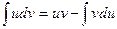 , за
, за  следует принять выражение:
следует принять выражение:
$$ 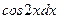
В интеграле  применяется формула интегрирования по частям в виде
применяется формула интегрирования по частям в виде 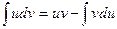 . Указать какую функцию необходимо принять за
. Указать какую функцию необходимо принять за  и какое выражение за
и какое выражение за  .
.
$$ 

В интеграле 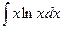 , чтобы применить формулу интегрирования по частям
, чтобы применить формулу интегрирования по частям 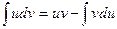 , за
, за  следует принять функцию:
следует принять функцию:
$$ 
В показательной форме комплексное число  имеет вид:
имеет вид:
$$ 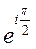
В показательной форме комплексное число (  ) имеет вид:
) имеет вид:
$$  .
.
В треугольнике с вершинами О(0;0), А(8;0) и В(0;6). Определить длину медианы ОМ:
$$5
В тригонометрической форме комплексное число (  ) имеет вид:
) имеет вид:
$$  .
.
В тригонометрической форме комплексное число  представимо в виде:
представимо в виде:
$$ 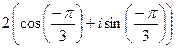 .
.
Вектор, параллельный прямой линии, которая проходит через точки  равен:
равен:
$$ 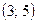
Векторы лежащие на одной прямой или на параллельных прямых называются:
$$ Коллинеарными
Вертикальная асимптота функции  есть прямая:
есть прямая:
$$ 
Вертикальная асимптота функции  имеет вид:
имеет вид:
$$ x=0
Вертикальная асимптота функции  .
.
$$ 
Выбрать характеристическое уравнение, соответствующее уравнению  :
:
$$ 
Вычислить  :
:
$$ 
Вычислить  :
:
$$ 2i
Вычислить 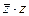 , если
, если 
$$ 5
Вычислить:  .
.
$$ 
Вычислить  :
:
$$ 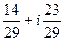
Вычислить:  .
.
$$ 0
Вычислить:  .
.
$$–11
Вычислить  .
.
$$ 70
Вычислить:  .
.
$$30
Вычислить:  .
.
$$ 6
Вычислите определитель: 
$$ 0
Вычислить  .
.
$$ 
Вычислить: 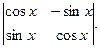
$$ 1
Вычислить  .
.
$$ 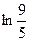
Вычислить  .
.
$$ 
Вычислить  :
:
$$ 
Вычислить 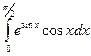
$$ 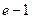
Вычислить  .
.
$$2 / 3
Вычислить  :
:
$$ 3
Вычислить 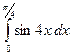 .
.
$$1 / 2
Вычислить алгебраическое дополнение А12 определителя 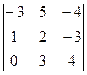 .
.
$$–4
Вычислить алгебраическое дополнение А32 определителя  .
.
$$ –22
Вычислить интеграл  :
:
$$ 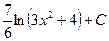
Вычислить интеграл 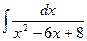 :
:
$$ 
Вычислить интеграл 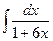 :
:
$$ 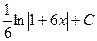
Вычислить интеграл  :
:
$$ 
Вычислить интеграл 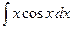 :
:
$$ 
Вычислите определенный интеграл 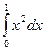 :
:
$$1 /3
Вычислить объем тела вращения фигуры, ограниченной линиями 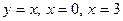 вокруг оси ОХ.
вокруг оси ОХ.
$$ 
Вычислить объем тела полученного вращением относительно оси ОХ фигуры, ограниченной кривыми 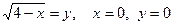 .
.
$$ 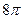
Вычислить площадь треугольника, отсекаемого прямой  от координатного угла.
от координатного угла.
$$ 6
Вычислить площадь фигуры, ограниченной кривыми  .
.
$$ 16
Вычислить площадь фигуры, ограниченной кривыми  .
.
$$ 
Вычислить площадь фигуры, ограниченной кривыми y = x  , 4y = x
, 4y = x  , x = 2, x = -2.
, x = 2, x = -2.
$$ 4
Вычислить предел 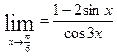 .
.
$$ 
Вычислить ранг матрицы  :
:
$$3
ГГГ
Горизонтальная асимптота функции  есть прямая:
есть прямая:
$$  .
.
ДДД
Дан вектор 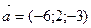 . Найти единичный вектор, вектора
. Найти единичный вектор, вектора  :
:
$$ 
Дан вектор  в виде разложения по базису
в виде разложения по базису  . Абсцисса этого вектора равна числу:
. Абсцисса этого вектора равна числу:
$$ -3
Дан вектор  . Проекция этого вектора на ось ОУ равна:
. Проекция этого вектора на ось ОУ равна:
$$ 3
Дан вектор  в виде разложения по базису
в виде разложения по базису  . Указать координаты этого вектора:
. Указать координаты этого вектора:
$$ 
Дан ряд  . Написать общий член ряда:
. Написать общий член ряда:
$$ 
Дан ряд  . Написать общий член ряда:
. Написать общий член ряда:
$$ 
Дана функция  . Вычислите
. Вычислите 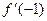 .
.
$$ -2
Дана функция  . Найти
. Найти  .
.
$$ 
Дана функция 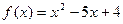 . Вычислите
. Вычислите 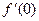 .
.
$$-5
Дана функция  . Вычислите
. Вычислите  .
.
$$  .
.
Дана функция  . Значение производных
. Значение производных  ,
,  :
:
$$ 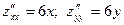
Дана функция  . Частная производная второго порядка
. Частная производная второго порядка  равна:
равна:
$$ 6
Дана функция  , частная производная второго порядка
, частная производная второго порядка  равна:
равна:
$$ 2
Дана функция  . Градиент функции z в точке
. Градиент функции z в точке  равен:
равен:
$$ 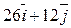
Дана функция  . Смешанная производная второго порядка
. Смешанная производная второго порядка 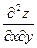 равна:
равна:
$$ -6
Даны вектора 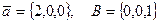 . Косинус угла между этими векторами равен:
. Косинус угла между этими векторами равен:
$$ 0
Даны векторы  ,
,  . Найти скалярное произведение векторов
. Найти скалярное произведение векторов  .
.
$$ 9
Даны векторы 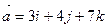 ,
, 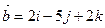 . Найти скалярное произведение векторов
. Найти скалярное произведение векторов  . $$ 0
. $$ 0
Даны векторы  (3;-2) и
(3;-2) и  (1;1). Найти вектор
(1;1). Найти вектор 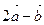
$$(5;-5)
Даны векторы 
 . Найти
. Найти  .
.
$$ (4;2)
Даны векторы  (1;-4) и
(1;-4) и  (-4;8). Найти длину вектора
(-4;8). Найти длину вектора  .
.
$$ 5
Даны векторы  (4;-1) и
(4;-1) и  (2;5). Найти вектор
(2;5). Найти вектор 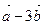 .
.
Дата добавления: 2015-01-05; просмотров: 328; Мы поможем в написании вашей работы!; Нарушение авторских прав |