A) теңдеудегі туындының жоғарғы ретін

$$$245 Дифференциалдық теңдеуді шешіңіз: . E)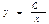

$$$246 Дифференциалдық теңдеуді шешіңіз: 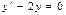. А)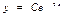

$$$247 Дифференциалдық теңдеуді шешіңіз: 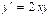. В)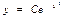

$$$248 Дифференциалдық теңдеуді шешіңіз: 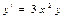С)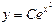

$$$249 Дифференциалдық теңдеуді шешіңіз: . D)

Е

$$$ 4Егер U-негізгі жиын, 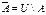болса, онда

D)
$$$ 5Егер U-негізгі жиын, 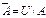болса, онда

E)

$$$ 6Егер U-негізгі жиын, 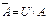болса, онда

A)
$$$ 7Егер U-негізгі жиын, 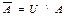болса, ондаB)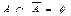

$$$ 17Егер X-жоғарыдан шенелген жиын, ал M оның жоғарғы шекарасы болса, онда B)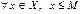
$$$ 18Егер X-төменнен шенелген жиын, ал m оның төменгі шекарасы болса, онда C)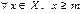
$$$ 19Егер X-шенелген жиын болса, онда

D)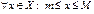

$$$ 20Егер M саны X-cандар жиынының ең үлкен элементі болса, онда Е)

$$$ 21Егер m саны X-cандар жиынының ең кіші элементі болса, онда A)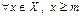

$$$ 25 Егер X=[1;2) болса, онда 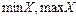табыңыз Е) жоқ

$$$ 26 Егер X=(2;3] болса, онда 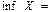A) 2
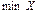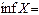$$$ 27 Егер X=(2;3) болса, онда және табыңыз B) -жоқ; 2
$$$ 28 Егер X=(2;3] болса, онда C) maxX=supX=3

$$$ 29 Егер y=f(x) функциясы D аймағында (қатаң) өспелі болса, онда D)

$$$ 30 Егер y=f(x) функциясы D аймағында (қатаң) кем-і болса, онда E)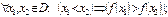

$$$ 31 Егер y=f(x) функциясы D аймағында кем-н болса, онда A)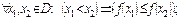

$$$ 32 Егер y=f(x) функциясы D аймағында өспейтін болса, онда B)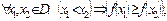

$$$ 33 Егер |q|<1 болса, онда C) 0

$$$ 34 Егер |q|>1 болса, онда 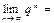D) ∞

$$$ 24 Егер X=[1;2) болса, онда 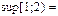D) 2

$$$ 36 Егер 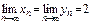және 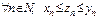болса, онда 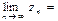A) 2

$$$ 44Егер 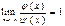тең áîëñà, îíäà

D) 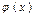ïåí ôóíêöèÿëàðû, 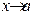ұмтылғанда, ýêâèâàëåíòті;

$$$45Егер áîëñà, îíäà

Å) ;

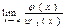$$$46 Егер 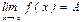, 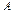-ақырлы сан болса, онда: A) 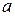-нүктесінің қандайда бір манайында шенелген функция

$$$47 Егер 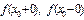біржақты шектері бар, бірақ теңдіктерінің ең болмағанда біреуі орындалмаса, онда функциясы 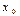нүктесінде B) 1 текті үзілістідеп аталады.

$$$48 Егер 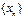-тізбегі шенелген, ал 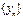-ақырсыз үлкен тізбек болса, онда: C)

$$$50 Егер E)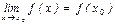

теңдігі орындалса, онда 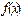функциясы 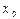нүктесінде үзіліссіз деп аталады

$$$51 Егер 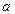нүктесіндегі функциясының біржақты шектерінің ең болмағанда біреуі жоқ немесе ақырсыз болса, онда 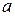нүктесінде 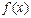функциясы

A) екінші текті үзілістідеп аталады

$$$52 Егер 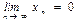және 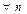үшін болса, онда: B)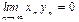

$$$56 Егер 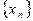-сандық тізбек жинақты болса, к4 ол: A) шенелген

$$$119 Егер 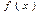функциясы 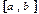кесіндісінде үзіліссіз болса, онда ол 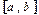-кесіндісінде: E) шенелген

$$$120 Егер берілген интервалда 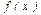фун-ң туындысы 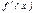теріс болса, онда функциясы осы интервалда: E) кемиді

$$$123 Егер 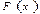функциясы аралығындадифференциалданса және мына теңдік орындалса:

E)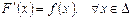

онда 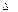аралығында функциясының 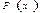функциясы алғашқы функциясы деп аталады.

$$$127 Егер 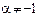болса, онда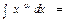

E)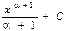

$$$151 Егер функциялары 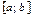аралығында интегралданса және 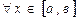, 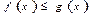теңсіздігі орындалса , онда:

А)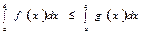

$$$152 Егер 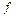функциясы 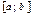аралығында үзіліссіз және 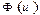қандайда бір оның алғашқы функциясы болса , онда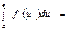

В)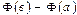

$$$153 Егер 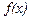функциясы жұп болса, онда 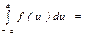C)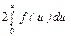

$$$154 Егер функциясы тақ болса, онда 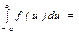В) 0

$$$163 Егер қисық : 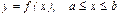берілсе, онда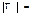

С)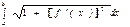

$$$164 Егер қисық полярлық координата түрінде берілсе : 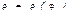, , 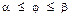онда В)

$$$165 Егер 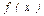функциясының 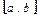аралығында таңбасын бірнеше рет өзгертетін болса, онда 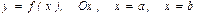сызықтармен шенелген жазық фигуранаң ауданын есептеу формуласын көрсетіңіз Е)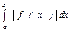

$$$198 Егер функциясының - стационар нүктесінде , 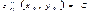болып, 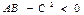, 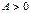шарты орындалса , онда 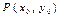нүктесінде функциясының C) минимумы болмайды

$$$199 Егер 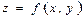функциясының 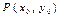- стационар нүктесінде 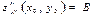, 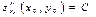болып, 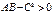, 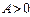шарты орындалса , онда 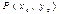нүктесінде функциясының D) локальді минимумі болады

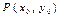$$$200 Егер функциясының - стационар нүктесінде , 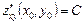болып, 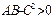, 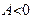шарты орындалса , онда нүктесінде функциясының Е)локальді максимумы болады

$$$202 Егер болса, онда 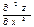табыңыз: В)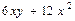

$$$203 Егер 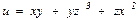болса, онда : С)

$$$204Егер 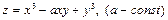болса, онда 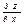: D)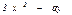

$$$205 Егер 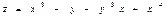болса, онда 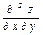亢: Е)

$$$206 функцияның толық дифференциалын: А)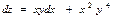

$$$207 Егер 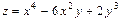.болса, онда 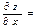В)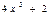

$$$ 223 Егер 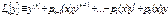- n- ші ретті дифференциалдық оператор болса, онда оның біртектілік қасиетін көрсетіңіз

Дата добавления: 2015-01-05; просмотров: 28; Нарушение авторских прав