А) - функциялары аралығында сызықты тәуелсіз және олардың әрқайсысы көрсетілген біртекті теңдеудің шешімдері

$$$ 233 Коэффициенттері тұрақты сызықтық біртекті -ші ретті , дифференциалдық теңдеудің жалпы шешімін көрсетіңіз

С) , - функциялары аралығында көрсетілген біртекті теңдеудің фундаментальды шешімдер жүйесі

$$$ 234 Коэффициенттері тұрақты сызықтық біртекті емес -ші ретті , дифференциалдық теңдеудің жалпы шешімін көрсетіңіз

Д) , - берілген диф. теңдеудің қандай да бір дербес шешімі; - біртекті диф. теңдеудің жалпы шешімі

Л

$$$162

параметірлік түрде берілген қисықтың ұзындығы

В)

$$$166 қисығының ұзындығын табыңыз: А)

$$$172 Меншіксіз интеграл жинақты болса, оны есептеу керек: В)

$$$173 Меншіксіз интеграл жинақты болса, оны есептеу керек: С) 4

$$$174 Меншіксіз интеграл жинақты болса, оны есептеу керек: D)

$$$175 Меншіксіз интеграл жинақты болса, оны есептеу керек: Е) жинақсыз

$$$176 Меншіксіз интеграл жинақты болса, оны есептеу керек: А)3

$$$177 Меншіксіз интеграл жинақты болса, оны есептеу керек: В)жинақсыз

$$$178 Меншіксіз интеграл жинақты болса, оны есептеу керек: С) жинақсыз

$$$179 Меншіксіз интеграл жинақты болса, оны есептеу керек: D) жинақсыз

$$$180 Меншіксіз интеграл жинақты болса, оны есептеу керек: Е) жинақсыз

$$$181 Меншіксіз интеграл жинақты болса, оны есептеу керек: А) жинақсыз

$$$182 Меншіксіз интеграл жинақты болса, оны есептеу керек: В)

$$$183 Меншіксіз интеграл жинақты болса, оны есептеу керек: С)

$$$184 Меншіксіз интеграл жинақты болса, оны есептеу керек: 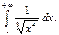D) 3

$$$185 Меншіксіз интеграл жинақты болса, оны есептеу керек: 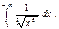Е)

$$$186 Меншіксіз интеграл жинақты болса, оны есептеу керек: А) жинақсыз

$$$187 Меншіксіз интеграл жинақты болса, оны есептеу керек: 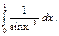В)жинақсыз

$$$188 Меншіксіз интеграл жинақты болса, оны есептеу керек: С)

$$$189 Меншіксіз интеграл жинақты болса, оны есептеу керек: D)

$$$190 Меншіксіз интеграл жинақты болса, оны есептеу керек: Е)

$$$237 Мына бірінші ретті дифференциалдық теңдеудің қайсылары айнымалдары ажыратылатын дифференциалдық теңдеу? В)

$$$238 Мына бірінші ретті дифференциалдық теңдеудің қайсылары айнымалдары ажыратылатын дифференциалдық теңдеу: С)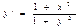

$$$239 Мына бірінші ретті дифференциалдық теңдеудің қайсылары айнымалдары ажыратылатын дифференциалдық теңдеу: D)

$$$240 Мына бірінші ретті дифференциалдық теңдеудің қайсылары айнымалдары ажыратылатын дифференциалдық теңдеу: Е)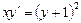

$$$241 Мына бірінші ретті дифференциалдық теңдеудің қайсылары айнымалдары ажыратылатын дифференциалдық теңдеу: А)

$$$242 Мына бірінші ретті дифференциалдық теңдеудің қайсылары сызықтық дифференциалдық теңдеу: В)

$$$243 Мына бірінші ретті дифференциалдық теңдеудің қайсылары сызықтық дифференциалдық теңдеу: С)

$$$244 Мына бірінші ретті дифференциалдық теңдеудің қайсылары сызықтық дифференциалдық теңдеу: Д)

Н

$$$ 225 n- ші ретті сызықтық біртекті емес дифференциалдық теңдеуді көрсетіңіз

Е)

$$$ 226 n- ші ретті сызықтық біртекті дифференциалдық теңдеуді көрсетіңіз

А)

П

$$$ 218 теңдеуі толық дифференциалдық теңдеу болуы үшін функциясы қандай шартты қанағаттандыруы керек екенін көрсетіңіз

C)

$$$ 219 теңдеуі толық дифференциалдық теңдеу болуы үшін қажетті және жеткілікті шартты көрсетіңіз D)

$$$ 321 Поляр координаталарына көшу арқылы интегралын есетеңіз, мұндағы A)

С

$$$291 -тұрақты болса, онда

А)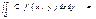

Т

$$$ 250 Тå»äåóäi» æàëïû øåøiìií òàáû»ûç : = .

E) y = +C

$$$ 251 Òå»äåóäi» æàëïû øåøiìií òàáû»ûç :

= А)y = arctg x + C

$$$ 252 Ò»äåóäi» æàëïû øåøiìií òàáû»ûç :

= В) y = arcsin x + C

$$$ 253 Òå»äåóäi» æàëïû øåøiìií òàáû»ûç:

= . С) y = 2 + C

$$$ 254 Òå»äåóäi» æàëïû øåøiìií òàáû»ûç : , x 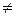0. D) y = Cx

$$$ 255 Òå»äåóäi» æàëïû øåøiìií òàáû»ûç: , y 0. E) x² + y² = C

$$$ 256 Òå»äåóäi» æàëïû øåøiìií òàáû»ûç :

+ 2xy = 0. A) y = C e

$$$ 257 Òå»äåóäi» æàëïû øåøiìií òàáû»ûç:

= 2x. В)y =

$$$ 258 Òå»äåóäi» æàëïû øåøiìií òàáû»ûç:

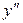=cos2 x. С)

$$$ 259 Òå»äåóäi» æàëïû øåøiìií òàáû»ûç :

= - . D) y = ln + C₁x + C₂

$$$ 260 Òå»äåóäi» æàëïû øåøiìií òàáû»ûç :

– 7 + 6 = 0 Е) y = C₁e^6x +

$$$ 261 Òå»äåóäi» æàëïû øåøiìií òàáû»ûç : 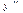- 9y = 0

A) y = C₁e^3x + C₂e^-3x

$$$ 262 Òå »äåóäi» æàëïû øåøiìií òàáû»ûç :

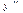- 4 + 4y = 0. B) y = C₁e^2x

$$$ 264 Òå»äåóäi» æàëïû øåøiìií òàáû»ûç : - 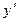= 0

D) y = C₁ e^-x + C₂e^x

$$$ 265 Òå»äåóäi» æàëïû øåøiìií òàáû»ûç 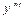+ = 0

E) y = C₂x+C₃e^-x

$$$ 266 Òå»äåóäi» æàëïû øåøiìií òàáû»ûç : 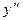+ 9y = 0

A) y = C₁ cos 3x + C₂ sin 3x

$$$ 267 Òå»äåóäi» æàëïû øåøiìií òàáû»ûç:

- 4 + 13y = 0 В) y = e^2x (C₁cos 3x + C₂ sin 3x)

$$$ 268 Òå»äåóäi» æàëïû øåøiìií òàáû»ûç : - = 0.

C) y = C₁ + C₂e^x

$$$ 269 Òå»äåóäi» æàëïû øåøiìií òàáû»ûç: tg x = y - 5.

D) y = C sin x + 5

$$$ 270 äèôôåðåíöèàëäûº òå»äåóäi» æàëïû øåøiìií òàбу керек:

E)

$$$ 271 Òå»äåóäi øåøу керек:

А)

$$$ 272 Òå»äåóäi øåøу керек:

B)

$$$ 273 Òå»äåóäi øåøу керек:

С)

$$$ 274 Òå»äåóäi øåøу керек:

D)

$$$ 275 Òå»äåóäi øåøу керек:

Е)

$$$ 276 Òå»äåóäi øåøу керек:

A)

$$$ 277 Òå»äåóäi øåøу керек:

В)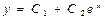

$$$ 278 Òå»äåóäi øåøу керек:

C)

$$$ 279 Òå»äåóäi øåøу керек:

D)

$$$ 280 Òå»äåóäi øåøу керек:

Е)

$$$ 281 Òå»äåóäi øåøу керек:

А)

$$$ 282 Òå»äåóäi øåøу керек:

B)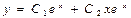

$$$ 283 Òå»äåóäi øåøу керек:

C)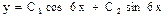

$$$ 284 Òå»äåóäi øåøу керек:

Д)

$$ 285 Òå»äåóäi øåøу керек:

E)

$$$ 286 Òå»äåóäi øåøу керек:

А)

Ш

$$$57 Шекті табыңыз: 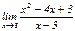. В) 2

$$$58 Шекті табыңыз: C)

$$$59 Шекті табыңыз: D)

$$$60 Шекті табыңыз: . E)

$$$61 Шекті табыңыз: . A)

$$$ 77Шекті табыңыз: В)

Дата добавления: 2015-01-05; просмотров: 38; Нарушение авторских прав