
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
С) , С-сан
$$$ 224Егер 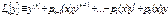 - n- ші ретті дифференциалдық оператор болса, онда оның аддитивтік қасиетін көрсетіңіз
- n- ші ретті дифференциалдық оператор болса, онда оның аддитивтік қасиетін көрсетіңіз
D) 
$$$ 227 Егер  интервлында
интервлында  -ші ретке дейінгі туындылары бар
-ші ретке дейінгі туындылары бар  функциялары осы интервалда сызықты тәуелді болса, онда
функциялары осы интервалда сызықты тәуелді болса, онда
B) 
$$$ 232 Егер коэффициенттері тұрақты сызықтық біртекті  -ші ретті
-ші ретті  дифференциалдық теңдеудің сипаттаушы
дифференциалдық теңдеудің сипаттаушы  теңдеуінің түбірлері:
теңдеуінің түбірлері:  әртүрлі, өзара тең емес сандар болса, онда
әртүрлі, өзара тең емес сандар болса, онда  дифференциалдық теңдеудің фундаментальды ше-р жүйесін көрсетіңіз
дифференциалдық теңдеудің фундаментальды ше-р жүйесін көрсетіңіз
В) 
$$$ 287 Егер
 екі еселі интегралдағы айн-ы
екі еселі интегралдағы айн-ы  ,
,  , арқылы ауыстырса, онда Якобиан: В)
, арқылы ауыстырса, онда Якобиан: В)  тең болады
тең болады
$$$288 Егер
 (мұндағы
(мұндағы  және
және  шекаралық нүктелерінде ғана қиылысатын аймақтар) болса, онда
шекаралық нүктелерінде ғана қиылысатын аймақтар) болса, онда 
C) 
$$$ 301
Егер  және
және  пластинка бетінің ты-ы болса, онда
пластинка бетінің ты-ы болса, онда  интегралы нені өрнектейді? А) пластинканың массасын;
интегралы нені өрнектейді? А) пластинканың массасын;
$$$ 302
Егер G аймағы  ,
,  ,
,  ,
, 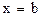 , где
, где  ,
,  сызықтарымен шенелген болса (
сызықтарымен шенелген болса (  функциялары
функциялары  кесіндісінде үзіліссіз), онда
кесіндісінде үзіліссіз), онда 
B) 
$$ 303 Егер G аймағы 
 сызықтарымен шенелген болса, онда
сызықтарымен шенелген болса, онда  және
және  функциялары
функциялары  кесіндісінде үзіліссіз)
кесіндісінде үзіліссіз) 
C) 
$$$ 331 Егер  ,
,  ,
,  болса, онда
болса, онда  интегралды есептеңіз А)
интегралды есептеңіз А) 
$$$ 333 Егер  ,
,  ,
,  болса, онда
болса, онда  интегралын есептеңіз C) 1
интегралын есептеңіз C) 1
$$$ 335 Егер  ,
,  ,
,  болса, онда
болса, онда  интегралын есептеңіз Е) 3
интегралын есептеңіз Е) 3
И
$$$121 Интегралды есептеңіз:  .
.
E) 
$$$122 Интегралын есептетеңіз:  .
.
E) 
$$$ 88Кез-келген  ñàíû ¾øií
ñàíû ¾øií 
Ñ)  ;
;
$$$ 228 Кез келген аралықта сызықты тәуелсіз функциялар жүйесін көрсетіңізС)  ,
,  - өзара тең емес әртүрлі сандар
- өзара тең емес әртүрлі сандар 
$$$ 229 Кез келген аралықта сызықты тәуелсіз фун-р жүйесін көрсетіңіз D) 
$$$ 230 Кез келген аралықта сызықты тәуелсіз фун-р жүйесін көрсетіңіз Е) 
$$$ 231 Коэффициенттері тұрақты сызықтық біртекті  -ші ретті
-ші ретті  ,
,  дифференциалдық теңдеудің фундаментальды (іргелі) шешімдер жүйесі қандай шарттарды қанағаттандырады?
дифференциалдық теңдеудің фундаментальды (іргелі) шешімдер жүйесі қандай шарттарды қанағаттандырады?
Дата добавления: 2015-01-05; просмотров: 300; Мы поможем в написании вашей работы!; Нарушение авторских прав |