
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные уравнения прямолинейного движения и движения по окружности
Равномерное прямолинейное движение:
Ускорение:  Скорость:
Скорость: 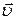 = const;
Перемещение: = const;
Перемещение: 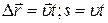 ;
Координата: x = x0 + ;
Координата: x = x0 + 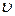 t t
| Равномерное движение по окружности: Ускорение: ε = 0; an =v2/R = ω2R = ωv: a = an Угловая скорость: ω =Δ φ /Δ t =2π ν= 2π /T; v = ωR; ω = ω0 +εt; Путь: s =Rφ ; Угол поворота: φ = 2πn; Период и частота: T=t/n; ν = n/t = T-1; |
Равнопеременное прямолинейное движение:
Тангенциальное ускорение:
at=const
Нормальное ускорение;
an=0;
Полное ускорение
a=const;
Скорость:
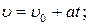 Средняя скорость:
Средняя скорость:
 v
Путь: v
Путь:

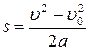 Координата:
Координата:

| Равнопеременное движение по окружности:
Угловое ускорение: ε = const;
Тангенциальное ускорение at = ε r;
Нормальное ускорение:
 Полное ускорение:
Полное ускорение:
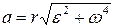 Угловая скорость:
Угловая скорость:
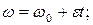 Средняя угловая скорость:
Средняя угловая скорость:
 Угол поворота
Угол поворота
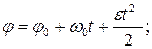
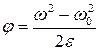 Пройденный путь:
s = rφ; φ= 2πn
Пройденный путь:
s = rφ; φ= 2πn
|
Пример 1. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид х = А + В t + С t3, где А = 4 м, В = 2 м/с, С = - 0,5 м/с2. Для момента времени t1 = 2 с определить: 1) координату х1 точки; 2) мгновенную скорость V1; 3) мгновенное ускорение а1.
Решение. Найдем координату точки, для которой известно кинематическое уравнение движения, подставив в уравнение движения вместо t заданное значение t1:
х1 = А + В t1 + С t13; х1 = 4 м.
Мгновенную скорость V в произвольный момент времени t найдем, продифференцировав координату х по времени:
V =  = B + 3Ct2.
= B + 3Ct2.
Тогда в заданный момент времени мгновенная скорость:
V1 = B + 3Ct21; V1 = - 4 м/с.
Знак минус указывает на то, что в момент времени t1 = 2 с точка движется в отрицательном направлении координатной оси.
Мгновенное ускорение в произвольный момент времени найдем, взяв вторую производную от координаты по времени:
a = 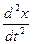 = 6Ct.
= 6Ct.
Мгновенное ускорение в заданный момент времени равно:
a1 = 6Ct1; a1 = - 6 м/c2.
Знак минус указывает на то, что направление вектора ускорения совпадает с отрицательным направлением координатной оси.
 Пример 2.Тело вращается вокруг неподвижной оси по закону, выражаемому формулой φ = 10 + 20 t - 2 t2 (рис. 1). Найдите по величине и направлению полное ускорение точки, находящейся на расстоянии R = 0,1 м от оси вращения, для момента времени t1 = 4 с.
Пример 2.Тело вращается вокруг неподвижной оси по закону, выражаемому формулой φ = 10 + 20 t - 2 t2 (рис. 1). Найдите по величине и направлению полное ускорение точки, находящейся на расстоянии R = 0,1 м от оси вращения, для момента времени t1 = 4 с.
Условие:
φ=10+20t-2t2;
R=0,1 м;
t1=4 c;
a - ? α - ?
Решение. Точка вращающегося тела описывает окружность. Полное ускорение точки определяется геометрической суммой тангенциального и нормального ускорения:
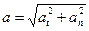 (1)
(1)
Тангенциальное и нормальное ускорения точки вращающегося тела выражаются формулами:
а t= εR; (2)
an = ω2R, (3)
где ω - угловая скорость тела; ε - его угловое ускорение; R - расстояние от оси вращения.
Подставляя выражения аt и аn в формулу (1) находим:
a = R  . (4)
. (4)
Угловая скорость вращающегося тела равна первой производной от угла поворота по времени
ω = 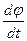 = 20 – 4t.
= 20 – 4t.
В момент времени t = 4 с угловая скорость ω = 4 с-1.
Угловое ускорение вращающегося тела равно первой производной от угловой скорости по времени:
ε = 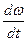 = - 4 c-2.
= - 4 c-2.
Подставляя найденные и заданные значения в формулу (4) получим:
a = 1,65 м/c2.
Направление полного ускорения можно определить, если найти углы, которые векторы ускорения составляют с касательной к траектории или нормалью к ней:
cos α =  . (5)
. (5)
По формулам (2) и (3) найдем значения аt и an:
at = - 0,4 /c2; an = 1,6 /c2 .
Подставив эти значения и значения полного ускорения в формулу (5), получим:
cos α = 0,242; α = 760.
Дата добавления: 2014-10-31; просмотров: 350; Мы поможем в написании вашей работы!; Нарушение авторских прав |