
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Применение теоремы Гаусса к расчету электрических полей
| Система зарядов | Напряженность поля | II потенциал |
| Точечный заряд Q | E = Q/4πε0r2 | φ =Q/4πε0r φ∞ = 0 |
| Равномерно заряженная бесконечная плоскость с поверхностной плотностью зарядов σ | E = σ/2ε0 | 
|
| Две равномерно разноименно заряженные бесконечные плоскости, расположенные на расстоянии d | 0 ≤ r ≤ d: E= 0 r < 0; r > d: E = σ/ε0 | 
|
| Равномерно заряженная сфера радиусом R | 0 < r < R: E = 0 r = R: E = Q/4πε0R2 r > R: E = Q/4πε0r2 | 0 < r ≤ R: φ = Q/4πε0R r > R: φ = Q/4πε0r |
| Равномерно объемно заряженный шар, радиусом R | 0 < r < R: E = Qr/4πε0R3 r = R: E = O/4πε0R2 r > R: E = Q/4πε0r2 | 0 < r < R:
 r = R: φ = Q/4πε0R
r > R: φ = Q/4πε0r r = R: φ = Q/4πε0R
r > R: φ = Q/4πε0r
|
| Равномерно заряженный бесконечный цилиндр радиуса R (нить) с линейной плотностью заряда τ | r < R: E = 0 r = R: E = τ/2πε0R; r > R: E = τ/2πε0r | r < R: φ = τ/2ε0
r > R: 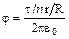
|
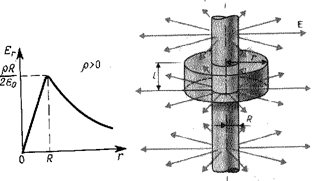
Пример 11.В вакууме имеется скопление зарядов в форме длинного цилиндра радиуса R = 2 см (рис. 11). Объемная плотность зарядов постоянна и равна ρ = 2 мКл/м3. Найти напряженность поля в точках 1 и 2, лежащих на расстояниях r1 = 1,0 см и r2 = 2,0 см от оси цилиндра. Построить график Е(r).
 |
Условие:
R = 2 см = 0,02 м;
r1 = 1,0 см =0,01 м;
r2= 2,0 см = 0,02 м;
Е1 - ? Е2 - ? Е(r) - ?
Решение. Поле создано зарядом, равномерно распределенным по объему. Конфигурация зарядов позволяет считать, что поле обладает осевой симметрией: силовые линии - прямые и в любой плоскости, перпендикулярной оси цилиндра радиальны. Предполагаемая симметрия позволяет искать напряженность с помощью теоремы Гаусса. Вспомогательной поверхности следует придать форму цилиндрической поверхности, коаксиальной заряду.
Характер функциональной зависимости Е(г) для точек лежащих внутри и вне объемного заряда различен. Поэтому следует провести две вспомогательные поверхности S1 и S2 с радиусами r1 < R и r2 > R. Для каждой поверхности теорема Гаусса может быть записана в виде
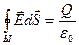 (1)
(1)
Боковая поверхность вспомогательного цилиндра и его торцы находятся в заведомо разных условий относительно силовых линий поля, причем во всех точках торцов Е  dS = π/2 и поток вектора напряженности сквозь торцевые поверхности равен нулю. На боковых поверхностях S1,2 бок нормаль совпадает с направлением радиуса-вектора, поэтому EdS = ErdS и
dS = π/2 и поток вектора напряженности сквозь торцевые поверхности равен нулю. На боковых поверхностях S1,2 бок нормаль совпадает с направлением радиуса-вектора, поэтому EdS = ErdS и

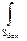 ErdS. (2)
ErdS. (2)
Все точки боковой поверхности находятся в одинаковых условиях относительно заряда, что позволяет считать Еr(г) постоянной величиной. Тогда
ErdS = Er2πrh, (3)
где r и h - радиус и высота вспомогательной поверхности.
Сумма зарядов, охваченных вспомогательной поверхностью, стоящая в правой части выражения (3), зависит от радиуса вспомогательной поверхности.
При r < R Q = ρπr2h, (4)
где r – расстояние от оси цилиндра до точки, в которой определяется напряженность поля и одновременно радиус вспомогательной поверхности S1.
Подставляя выражение (3) в (1) и заменяя интеграл по замкнутой поверхности S1 правой частью равенства (4) получаем
E12πrh = ρπr2h/ε0,
откуда E1 = ρr/2ε0, (5)
Е1 = 1,1·103 В/м.
При r > R Q = ρπR2 h .
Подставляя (3) в (31) и заменяя интеграл по замкнутой поверхности S2 правой частью равенства (4) получаем
E22πrh = τπR2h/ε0.
Откуда E2 = ρR2/2ε0r. (6)
Е2 = 1,5·103 В/м.
Для построения графика Е(г) на оснований выражений (5) и (6) целесообразно рассчитать Еr при г = R: Е(R) = ρR/2ε0 = 2,3∙103 В/м.
Расчет по формулам (5) и (6) дает один и тот же результат, так как напряженность на этой поверхности не терпит разрыва. Графическая зависимость Е(г) показана на рис. 11.
ТЕМА 9. ДИЭКТРИКИ, ПРОВОДНИКИ И КОНДЕНСАТОРЫ
9.1. Диэлектрики. Электрическое поле в диэлектриках
Электрический момент диполя: 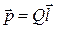 где
где  – плечо диполя – плечо диполя
|
Поляризованность: 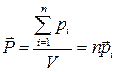 P = σ´,
где V – объем диэлектрика;
pi -дипольный момент i -й молекулы;
n0 – концентрация молекул;
σ´ - поверхностная плотность связанных зарядов. P = σ´,
где V – объем диэлектрика;
pi -дипольный момент i -й молекулы;
n0 – концентрация молекул;
σ´ - поверхностная плотность связанных зарядов.
|
| Связь между поляризованностью и напряженностью электростатического поля: P = æε0E, где æ > 0 - диэлектрическая восприимчивость вещества |
| Связь между диэлектрической проницаемостью и диэлектрической восприимчивостью вещества: ε = 1 + æ |
Связь между векторами электрического смещения и напряженностью электростатического поля:
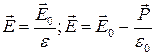 .
Связь между векторами электростатического смещения, напряженностью и поляризованностью: .
Связь между векторами электростатического смещения, напряженностью и поляризованностью:
 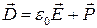
|
Элементарный поток вектора электрического смещения через площадку:
dФD = 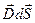 = DdScos α = DndS,
где = DdScos α = DndS,
где 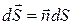 –вектор, модуль которого равен dS, а направление совпадает с нормалью к площадке;
Dn –составляющая вектора –вектор, модуль которого равен dS, а направление совпадает с нормалью к площадке;
Dn –составляющая вектора  по направлению нормали n к площадке по направлению нормали n к площадке
|
Теорeмa Гаусса для электростатического поля в диэлектрике:
Фd =  = =  DdScos α = DdScos α =  DndS = DndS = 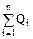 ,
где ,
где 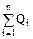 - алгебраическая сумма Qi, заключенных внутри замкнутой поверхности свободных электрических зарядов. Интегрирование ведется по всей поверxности. - алгебраическая сумма Qi, заключенных внутри замкнутой поверхности свободных электрических зарядов. Интегрирование ведется по всей поверxности.
|
9. 2. Электроемкость проводникoв и конденсаторов
Электроемкость уединенного проводника:  где Q–заряд, сообщенный проводнику, φ - потенциал проводника.
Электроемкость проводника, помещенного в диэлектрик: C = εC0
Электроемкость шарового проводника: C = 4πε0εR
где R–радиус шара; ε – диэлектрическая проницаемость среды
где Q–заряд, сообщенный проводнику, φ - потенциал проводника.
Электроемкость проводника, помещенного в диэлектрик: C = εC0
Электроемкость шарового проводника: C = 4πε0εR
где R–радиус шара; ε – диэлектрическая проницаемость среды
|
Электроемкость конденсатора: C = 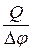 ,
где Q – заряд, сообщенный одной из обкладок;
∆φ - разность потенциалов между обкладками ,
где Q – заряд, сообщенный одной из обкладок;
∆φ - разность потенциалов между обкладками
|
Емкость плоского конденсатора:  где S - площадь каждой пластины конденсатора;
d – расстояние между пластинами
где S - площадь каждой пластины конденсатора;
d – расстояние между пластинами
|
Емкость цилиндрического конденсатора:  ,
где l – длина обкладок конденсатора;
r1 и r2 - радиусы полых коаксиальных цилиндров ,
где l – длина обкладок конденсатора;
r1 и r2 - радиусы полых коаксиальных цилиндров
|
Емкость сферического конденсатора:  где r1 и r2 - радиус концентрических сфер
где r1 и r2 - радиус концентрических сфер
|
Емкость системы конденсаторов
последовательное соединение: 1/ C = 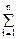 1/ Ci;
параллельное соединение: C = 1/ Ci;
параллельное соединение: C = 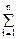 Ci,
где Ci - емкость i-го конденсатора, n - число конденсаторов в батарее. Ci,
где Ci - емкость i-го конденсатора, n - число конденсаторов в батарее.
|
8.3 Энергия системы точечных электрических зарядов, заряженных проводников и конденсаторов. Энергия электростатического поля. Объемная плотность энергии. Пондермоторные силы.
Энергия взаимодействия системы точечных зарядов: Wn = 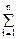 Qiφi/2,
где φi - потенциал, создаваемый в той точке, где находится заряд Qi всеми зарядами, кроме i–го Qiφi/2,
где φi - потенциал, создаваемый в той точке, где находится заряд Qi всеми зарядами, кроме i–го
|
| Энергия уединенного заряженного проводника: Wn = C2/2φ = Qφ/2 = Q2/2C, где Q– заряд ; C –электроемкость, φ –потенциал проводника |
| Энергия заряженного конденсатора: Wn = C2/2∆φ = Q∆φ/2 = Q2/2C, где ∆φ - разность потенциалов между обкладками |
Энергия электростатического поля плоского конденсатора (однородное поле):  ,
Где S– площадь одной из пластин; V = Sd - объем конденсатора ,
Где S– площадь одной из пластин; V = Sd - объем конденсатора
|
Объемная плотность энергии:
w = 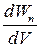 ; w = εε0E2/2 = D2/2 εε0 = ED/2,
где D - электрическое смещение ; w = εε0E2/2 = D2/2 εε0 = ED/2,
где D - электрическое смещение
|
Энергия электрического поля Wn = 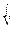 w dV w dV
|
| Силы притяжения между двумя разноименно заряженными обкладками плоского конденсатора (пондермоторные силы): F = Q2/(2 εε0S) = σ2S/(2 εε0 )= εε0E2S/2 |
Пример 12.Между обкладками плоского конденсатора, заряженного до разности потенциалов U = 1,5 кВ, зажата парафиновая пластинка (ε = 2) толщиной d = 5 мм. Определить поверхностную плотность связанных зарядов на парафине.
Условие:
U = 1,5 кВ = 1,5∙103 В;
ε = 2;
d = 5 мм = 5·10-3 м;
σ′ - ?
Решение. Вектор электрического смещения D =ε0E +P, где Е – вектор напряженности электрического поля, Р – вектор поляризации.
Так как векторы D и Е нормальны к поверхности диэлектрика, то D = Dn, E = En.
Тогда можно записать D = ε0E + P, где Р = σ′ , т.е. равна поверхностной плотности связанных зарядов диэлектрика. Тогда
σ′ = D – εε0E.
Учитывая, что D = εε0E и E = U/d, где d – расстояние между обкладками конденсатора, найдем
σ′ = (ε - 1)ε0Е = ε0(ε - 1)U/d =2,65 мкКл/м2.
Пример 13.Определить ускоряющую разность потенциалов Δφ, которую должен пройти в электрическом поле электрон, чтобы его скорость возросла от v1 = 1,0 Мм/с до v2 = 5,0 Мм/с.
Условие:
v1 = 1,0 Мм/с = 1,0·106 м/с;
v2 = 5,0 Мм/с = 5,0·106 м/с ;
е = 1,6·10-19 Кл;
m = 9,1·10-31 кг;
Δφ - ?
Решение. Работа, совершаемая силами электростатического поля при перемещении заряда из точки 1 в точку 2
А = е Δφ. (1)
С другой стороны, она равна изменению кинетической энергии электрона
А = W2 – W1 = mv22/2 - mv12/2. (2)
Приравняв выражения (1) и (2), найдем ускоряющую разность потенциалов
Δφ = m (v22 – v12)/2e = 68, 3 В.
Пример 14.К пластинам плоского воздушного конденсатора приложена разность потенциалов Δφ1 = 1,5 кВ. Площадь пластин S =150 cм2 и расстояние между ними d = 5,0 мм. После отключения конденсатора от источника напряжения в пространство между пластинами внесли стекло (ε = 7). Определить: 1) разность потенциалов между пластинами после внесения диэлектрика; 2) емкость конденсатора С1 и С2 до и после внесения диэлектрика; 3) поверхностную плотность заряда σ на пластинах до и после внесения диэлектрика.
Условие:
Δφ1 = 1,5 кВ =1,5·103 В;
S = 150см2 = 1,5·10-2 м2;
d =5 мм = 5·10-3 м;
ε1 = 7, ε2 = 1;
Δφ2 - ? С1 -? С2 - ?
σ1 - ?, σ2 - ?
Решение. Так как Е1 = Δφ1/d =  до внесения диэлектрика и E2 = Δφ2/d =
до внесения диэлектрика и E2 = Δφ2/d =  после внесения диэлектрика, поэтому
после внесения диэлектрика, поэтому
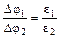 и
и
Δφ2 = ε1Δφ1/ε2 = 214 В.
Емкость конденсатора до и после внесения диэлектрика
С1 = 4πε1ε0S/d = 26,5 пФ, C2 = 4πε1ε0S/d = 186 пФ.
Заряд пластин после отключения от источника напряжения не меняется, т. е. Q = const. Поэтому поверхностная плотность заряда на пластинах до и после внесения диэлектрика
σ1 = σ2 = Q/S = C1Δφ1/S = C2Δφ2/S = 2,65 мкКл/м2.
ТЕМА 10. Постоянный электрический ток
10.1. Электрический ток, сила и плотность тока
Сила тока 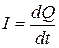 Единица силы тока - 1 А (ампер)
Сила постоянного тока:
Единица силы тока - 1 А (ампер)
Сила постоянного тока:  =const
Плотность тока: =const
Плотность тока:  Единица плотности тока - 1 А/м2
Заряд, переносимый через поперечное сечение проводника за время dt,:
dQ = ne<v>Sdt,
где n и e – концентрация и заряд носителей тока,
<v> - средняя арифметическая скорость упорядоченного движения электронов
Сила тока:
Единица плотности тока - 1 А/м2
Заряд, переносимый через поперечное сечение проводника за время dt,:
dQ = ne<v>Sdt,
где n и e – концентрация и заряд носителей тока,
<v> - средняя арифметическая скорость упорядоченного движения электронов
Сила тока:  Плотность тока:
Плотность тока: 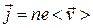
|
10.2. Электродвижущая сила (ЭДС). Напряжение
ЭДС:  ,
где Аст - работа сторонних сил по перемещению положительного заряда Qo
Работа сторонних сил ,
где Аст - работа сторонних сил по перемещению положительного заряда Qo
Работа сторонних сил 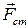 по перемещению заряда Q0 на замкнутом участке пути: по перемещению заряда Q0 на замкнутом участке пути:
 ,
где ,
где  - напряженность поля сторонних сил.
ЭДС, действующая в цепи,: - напряженность поля сторонних сил.
ЭДС, действующая в цепи,: 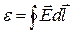 ЭДС на участке цепи
ЭДС на участке цепи 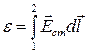
|
Сила, действующая на заряд в проводнике:
 Работа результирующей силы на участке 1-2 зарядом Q0:
Работа результирующей силы на участке 1-2 зарядом Q0:
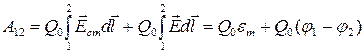 Для замкнутой цепи:
Для замкнутой цепи: 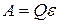 Напряжение на участке 1-2:
Напряжение на участке 1-2: 
|
10.3. Сопротивление проводников
Сопротивление однородного линейного проводник длиной l и площадью поперечного сечения S
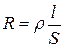 где
где  - удельное электрическое сопротивление
Единица измерения сопротивления – Ом
Единица измерения удельного сопротивления – Ом.м
Электрическая проводимость: - удельное электрическое сопротивление
Единица измерения сопротивления – Ом
Единица измерения удельного сопротивления – Ом.м
Электрическая проводимость:  Единица измерения электрической проводимости – См (сименс)
Удельная электропроводимость:
Единица измерения электрической проводимости – См (сименс)
Удельная электропроводимость: 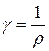 Единица измерения удельной электропроводности – См-1
Зависимость сопротивления от температуры:
Единица измерения удельной электропроводности – См-1
Зависимость сопротивления от температуры:
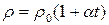
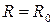  ,
где ,
где  - температурный коэффициент сопротивления, К-1, t – температура, 0С. - температурный коэффициент сопротивления, К-1, t – температура, 0С.
|
10.4. Последовательное и параллельное соединение проводников
| Соединение | Последовательное | Параллельное |
| Постоянная величина | I1 = I2 = …=In I=concs | U1=U2=…Un U=const |
| Суммируемая величина | Напряжение
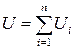
| сила тока

|
| Результирующее сопротивление |  
| 

|
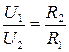
| 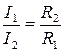
|
10.5. Закон Ома для однородного участка и замкнутой цепи.
Закон Ома для однородного участка цепи (не содержащего источника тока):
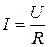 , ,
|
Закон Ома в дифференциальной форме: 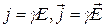
|
Закон Ома для замкнутой цепи:  где R –сопротивление внешней цепи,
r – внутреннее сопротивление источника тока.
Напряжение на внешней цепи:
где R –сопротивление внешней цепи,
r – внутреннее сопротивление источника тока.
Напряжение на внешней цепи: 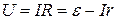 Ток короткого замыкания:
Ток короткого замыкания: 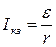
|
Закон Ома для батареи последовательно соединенных элементов:
 где n- число элементов в батарее
где n- число элементов в батарее
|
Закон Ома для батареи параллельно соединенных элементов:
 где n – число элементов в батарее
где n – число элементов в батарее
|
Закон Ома для смешанного соединения элементов в батарею:
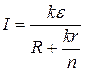 где k- число ветвей в батарее, n – число элементов в ветви.
где k- число ветвей в батарее, n – число элементов в ветви.
|
Закон Ома для неоднородного участка цепи (обобщенный закон Ома):
 где
где  - действующая на участке 1-2 ЭДС, - действующая на участке 1-2 ЭДС, 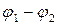 - разность потенциалов, приложенная к концам проводника. - разность потенциалов, приложенная к концам проводника.
|
10.6. Анализ обобщенного закона Ома
Источника тока нет: 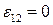
| Из ОЗО:

| Закон Ома для однородного участка цепи | |
Цепь замкнута

| Из ОЗО:
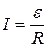 где R- сопротивление всей цепи
где R- сопротивление всей цепи
| Закон Ома для замкнутой цепи | |
| Цепь разомкнута: I=0 | Из ОЗО
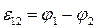 : :
| ЭДС в разомкнутой цепи равна разности потенциалов на ее концах |
10.7. Правила Кирхгофа для разветвленных цепей
Первое правило Кирхгофа:
Алгебраическая сумма токов, сходящихся в узле, равна нулю: 
|
Второе правило Кирхгофа:
В любом замкнутом контуре: 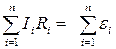
|
10.8. Работа и мощность тока
Элементарная работа электрического тока:
dA= Udq = IUdt = I2Rdt = 
|
Работа электрического тока:
A=  IUdt = IUdt =  I2Rdt = I2Rdt =   Единица работы – Дж (джоуль)
Внесистемная единица работы 1квт.ч= 3,6 МДж=.3,6.106 Дж
Единица работы – Дж (джоуль)
Внесистемная единица работы 1квт.ч= 3,6 МДж=.3,6.106 Дж
|
Работа постоянного электрического тока:
A= Uq = IUt = I2Rt = 
|
Мощность электрического тока:  Единица мощности – Вт (ватт)
Единица мощности – Вт (ватт)
|
Закон Джоуля - Ленца:
dQ= Udq = IUdt = I2Rdt =  Закон Джоуля –Ленца в интегральной форме:
Q==
Закон Джоуля –Ленца в интегральной форме:
Q==  IUdt = IUdt =  I2Rdt = I2Rdt =  
|
Закон Джоуля – Ленца для постоянного тока
Q= Uq = IUt = I2Rt = 
|
Закон Джоуля – Ленца в дифференциальной форме:
 ,
где ,
где 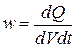 - удельная тепловая мощность тока - удельная тепловая мощность тока
|
Коэффициент полезного действия источника тока (КПД):

|
Пример 15.Найти сопротивление R , железного стержня диаметром d = 1 cм, если масса стержня m = 1 кг.
Условие:
d = 1 см = 0,01 м
v = 1 кг
 =0,087 мкОм.м=8,7.10-8 Ом.м.
=0,087 мкОм.м=8,7.10-8 Ом.м.
 =7,7.103 кг/м3
=7,7.103 кг/м3
R -?
Решение:
-Сопротивление стержня определяется по формуле
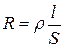 ,
,
где  удельное сопротивление железа,
удельное сопротивление железа,  -длина стержня и площадь поперечного сечения.
-длина стержня и площадь поперечного сечения.
Масса проволоки
 ,
,
где V - объем стержня,  - плотность стали.
- плотность стали.
Откуда длина стержня равна:
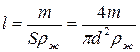 ,
,
поскольку площадь поперечного сечения стержня 
Тогда сопротивление стержня равно:
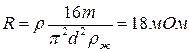
тЕМА 11. Магнитное поле
11.1. Основные характеристики магнитного поля
Вращающий момент сил на рамку с током в магнитном поле
 где pm-магнитный момент рамки с током,
где pm-магнитный момент рамки с током,
 - магнитная индукция; - магнитная индукция;
 - угол между нормалью к плоскости контура и вектором - угол между нормалью к плоскости контура и вектором 
|
Магнитный момент рамки с током  S – площадь поверхности контура (рамки);
S – площадь поверхности контура (рамки);
 - единичный вектор нормали к поверхности рамки - единичный вектор нормали к поверхности рамки
|
Магнитная индукция 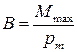 где Ммах – максимальный вращающий момент
Единица измерения индукции магнитного поля: Тл (тесла)= 1Н/А.м
где Ммах – максимальный вращающий момент
Единица измерения индукции магнитного поля: Тл (тесла)= 1Н/А.м
|
Магнитная индукция:  ,
где ,
где 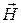 - вектор напряженности магнитного поля, А/м - вектор напряженности магнитного поля, А/м
 - магнитная проницаемость среды, - магнитная проницаемость среды,
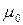  - магнитная постоянная - магнитная постоянная
|
Принцип суперпозиции (наложения) магнитных полей:
Магнитная индукция результирующего поля равна:  где Вi – магнитная индукция, создаваемая каждым током (движущимся зарядом) в отдельности
где Вi – магнитная индукция, создаваемая каждым током (движущимся зарядом) в отдельности
|
11.2. Закон Био -Савара – Лапласа и его применение
Закон Вио – Савара – Лапласа:
Магнитная индукция, создаваемая элементом проводника  с током I в некоторой точке равна: с током I в некоторой точке равна: 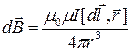 ,
где ,
где  - радиус-вектор, проведенный из элемента dl проводника в точку поля.
Скалярная форма записи закона Био – Савара – Лапласа имеет вид: - радиус-вектор, проведенный из элемента dl проводника в точку поля.
Скалярная форма записи закона Био – Савара – Лапласа имеет вид:
 где
где  - угол между - угол между  и и  . .
|
Магнитное поле прямого тока:  ,
где ,
где  - углы, под которыми из рассматриваемой точки поля видны начало и конец проводника,
r – расстояние до проводника
Магнитное поле бесконечного прямого тока: - углы, под которыми из рассматриваемой точки поля видны начало и конец проводника,
r – расстояние до проводника
Магнитное поле бесконечного прямого тока: 
|
Магнитное поле в центре кругового витка радиусом r: 
|
Магнитное поле на оси кругового витка на расстоянии b от его центра
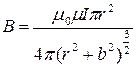 = =  где
где 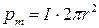 – магнитный момент витка с током I – магнитный момент витка с током I
|
Магнитное поле на оси соленоида конечной длины:
 ,
где n=N/L – число витков, приходящихся на единицу длины,
N, L – соответственно, число витков и длина соленоида, ,
где n=N/L – число витков, приходящихся на единицу длины,
N, L – соответственно, число витков и длина соленоида,
 - углы, под которыми из произвольной точки на оси соленоида видны его концы
Максимальная индукция в центре соленоида равна: - углы, под которыми из произвольной точки на оси соленоида видны его концы
Максимальная индукция в центре соленоида равна:
 ,
где r – радиус витка соленоида. ,
где r – радиус витка соленоида.
|

11.3. Закон Ампера. Взаимодействие параллельных токов.
Сила Ампера, действующая на элемент проводника  с током I с током I
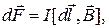  ,
где ,
где  - угол между - угол между  и и  .
Сила Ампера, действующая в магнитном поле на проводник конечной длины l с током I: .
Сила Ампера, действующая в магнитном поле на проводник конечной длины l с током I:  Сила Ампера, действующая в однородном магнитном поле на прямолинейный проводник:
Сила Ампера, действующая в однородном магнитном поле на прямолинейный проводник:  ,
где ,
где  -угол между током (вектором плотности тока) в проводнике и вектором -угол между током (вектором плотности тока) в проводнике и вектором 
|
Сила взаимодействия двух параллельных токов I1, I2 длиной l находящихся на расстоянии r друг от друга: 
|
11.4. Магнитное поле движущегося заряда
Магнитное поле  точечного заряда Q, свободно движущегося с нерялитивистской скоростью точечного заряда Q, свободно движущегося с нерялитивистской скоростью 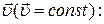
 ,
где ,
где  - радиус-вектор, проведенный из заряда Q к точке наблюдения, - радиус-вектор, проведенный из заряда Q к точке наблюдения,
 - угол между - угол между  и и  . .
|
11.5. Действие магнитного поля на движущийся заряд. Сила Лоренца. Движение заряженных частиц в магнитном поле
Сила Лоренца: 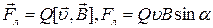 где Q – электрический заряд, движущийся со скоростью
где Q – электрический заряд, движущийся со скоростью 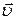 в магнитном поле с индукцией в магнитном поле с индукцией 
 угол между угол между 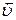 и и 
|
Формула Лоренца (сила, действующая на движущийся заряд со стороны магнитного поля с индукцией  и электрического поля с напряженностью и электрического поля с напряженностью  : : 
|
1. В однородном магнитном поле, если угол  между между 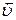 и и  равен 0 или равен 0 или  , сила Лоренца Fл=0, то частица движется равномерно и прямолинейно
2. Если угол , сила Лоренца Fл=0, то частица движется равномерно и прямолинейно
2. Если угол  = =  /2, тогда /2, тогда  , частица движется по окружности радиуса: , частица движется по окружности радиуса: 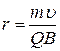 ,
период обращения частицы равен: ,
период обращения частицы равен: 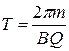 3. Заряженная частица движется со скоростью
3. Заряженная частица движется со скоростью 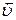 под углом под углом  к вектору к вектору  , возникает движение по спирали, ось которой параллельна магнитному полю.
Шаг винтовой линии: , возникает движение по спирали, ось которой параллельна магнитному полю.
Шаг винтовой линии: 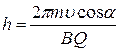 Радиус спирали равен:
Радиус спирали равен: 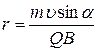
|
11.6 Теорема о циркуляции вектора  (закон полного тока для магнитного поля в вакууме) и ее применение к расчету магнитных полей
(закон полного тока для магнитного поля в вакууме) и ее применение к расчету магнитных полей
Теорема о циркуляции вектора  :
Циркуляция вектора :
Циркуляция вектора  по произвольному замкнутому контуру равна произведению магнитной постоянной по произвольному замкнутому контуру равна произведению магнитной постоянной 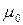 на алгебраическую сумму токов, охватываемых этим контуром: на алгебраическую сумму токов, охватываемых этим контуром:

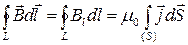 где
где  - составляющая вектора - составляющая вектора  в направлении касательной к контуру с учетом (выбранного обхода), в направлении касательной к контуру с учетом (выбранного обхода),
 - угол между векторами - угол между векторами  и и 
|
Магнитное поле на оси бесконечно длинного соленоида (цилиндрической катушки): 
|
Магнитное поле внутри тороида (кольцевой катушки): 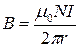 ,
где N- число витков, r – расстояние от центра тороида. ,
где N- число витков, r – расстояние от центра тороида.
|
Пример 16.Ток I =20 А, протекая по кольцу из медной проволоки сечением S = 1 мм2, создает в центре кольца напряженность Н = 178 А/м. Какая разность потенциалов U приложена к концам проволоки. образующей кольцо?
Условие:
I=20 A
S = 1 мм2 = 10-6 м2
Н = 178 А/м
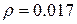 мкОм.м=1,7.10-8 Ом.м
мкОм.м=1,7.10-8 Ом.м
U-?
Дата добавления: 2014-10-31; просмотров: 448; Мы поможем в написании вашей работы!; Нарушение авторских прав |