
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ТЕМА 4. ОСНОВНОЕ УРАВНЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
4.1 Динамика вращательного движения
Момент инерции материальной точки относительно оси вращения:
J = mr2,
где m –масса,
r –расстояние до оси вращения.
Момент инерции системы материальных точек (тела): J =  ,
где ri – расстояние i–й материальной точки массой m до оси вращения.
В случае непрерывного распределения масс: J = ,
где ri – расстояние i–й материальной точки массой m до оси вращения.
В случае непрерывного распределения масс: J =  .
Теорема Штейнера: момент инерции тела массой m относительно неподвижной оси вращения, не проходящей через центр масс и параллельный оси вращения:
J = Jz + mr2,
где Jz –момент инерции тела относительно оси z, проходящей через центр масс,
r - расстояние между осями. .
Теорема Штейнера: момент инерции тела массой m относительно неподвижной оси вращения, не проходящей через центр масс и параллельный оси вращения:
J = Jz + mr2,
где Jz –момент инерции тела относительно оси z, проходящей через центр масс,
r - расстояние между осями.
|
4.2. Момент инерции тел правильной геометрической формы относительно неподвижной оси вращения
| Форма тела | Ось вращения проходит через: | Момент инерции |
| Однородный шар радиусом R и массой m | центр масс | 0,4mR2 |
| Круглый однородный цилиндр или диск радиусом R и массой m | центр масс перпендикулярно плоскости основания | 0,5mR2 |
| Тонкий обруч или кольцо радиусом R и массой m | центр масс перпендикулярно плоскости обруча | mR2 |
| Однородный тонкий стержень длиной L и массой m | центр масс стержня перпендикулярно стержню | mL2/12 |
| Однородный тонкий стержень длиной L и массой m | конец стержня перпендикулярно стержню | mL2/3 |
4.3 Момент силы, момент импульса. Основное уравнение динамики вращательного движения
Момент силы относитeльно произвольной точки:   где
где  – радиус-вектор, проведенный из этой точки в точку приложения силы – радиус-вектор, проведенный из этой точки в точку приложения силы  .
Модуль момента силы: M = Fl,
где l = r.sin α – плечо силы (кратчайшее расстояние между линией действия силы и осью вращения) .
Модуль момента силы: M = Fl,
где l = r.sin α – плечо силы (кратчайшее расстояние между линией действия силы и осью вращения)
|
Момент импульса твердого тела относительно оси вращения:   где
где  –радиус-вектор отдельной i - й частицы;
mi –радиус-вектор отдельной i - й частицы;
mi  - импульс этой частицы;
J- момент инерции тела относительно оси; - импульс этой частицы;
J- момент инерции тела относительно оси;  – угловая скорость – угловая скорость
|
Основное уравнение (закон) динамики вращательного движения твердого тела относительно неподвижной оси:   где ε – угловое ускорение;
Jz-момент инерции тела относительно оси
где ε – угловое ускорение;
Jz-момент инерции тела относительно оси
|
Закон сохранения момента импульса для замкнутой системы

|
| Работа при вращении тела: ΔA = MzΔφ где Δφ - угол поворота тела; Mz - момент силы относительно оси |
Кинетическая энергия тела, вращающегося вокруг неподвижной оси:  где J– момент инерции тела относительно оси,
ω - угловая скорость
Кинетическая энергия тела, катящегося по плоскости без скольжения:
где J– момент инерции тела относительно оси,
ω - угловая скорость
Кинетическая энергия тела, катящегося по плоскости без скольжения:
 где m– масса тела;
vc - скорость центра масс тела;
J – момент инерции тела относительно оси, проходящей через центр масс; ω –угловая скорость тела
где m– масса тела;
vc - скорость центра масс тела;
J – момент инерции тела относительно оси, проходящей через центр масс; ω –угловая скорость тела
|
Пример 7.Маховик, массу которого m = 5 кг можно считать распределенной по ободу радиуса r = 20 см, свободно вращается вокруг горизонтальной оси, проходящей через его центр с частотой n = 720 мин-1. При торможении маховик останавливается через Δt = 20 с. Определить тормозящий момент М и число оборотов N, которое сделает маховик до полной остановки.
Условие:
m = 5 кг
r = 20см =0,20 м
n =720 мин-1 = 12 с-1
Δt =20 с
М - ? N - ?
Решение. Если тормозящий момент постоянен, то движение маховика равнозамедленное, и основное уравнение динамики вращательного движения можно записать в виде:
 (1)
(1)
где  - изменение угловой скорости за интервал времени ∆t; М – искомый тормозящий момент.
- изменение угловой скорости за интервал времени ∆t; М – искомый тормозящий момент.
Число оборотов N может быть найдено как кинематически, так и по изменению кинетической энергии, равному работе совершаемой тормозящей силой.
Векторному уравнению (1) соответствует скалярное уравнение
J∆ω = M∆t, (2)
где ∆ω, M - модули соответствующих векторов.
Из условия задачи следует, что
∆ω = |ω – ω0|= ω0 =2πn (3)
Поскольку масса маховика распределена по ободу, момент инерции
J = mr2 (4)
Подставляя выражения (2), (3) в (1) получим
mr22πn = M∆t.
Откуда M = 2πnmr2/Δt = 0,75 H.м.
Векторы 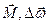 направлены в сторону противоположную вектору
направлены в сторону противоположную вектору 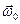 .
.
Угловое перемещение, пройденное маховиком до остановки
φ = ω0∆t – ε∆t2/2. (5)
Учитывая, что ω = ωo - ε∆t = 0 преобразуем выражение (6)
φ = ω0∆t/2.
Так как φ = 2πN, ω =2πn, где N - число оборотов, которое делает маховик до полной остановки, окончательно получим
N = nt/2 = 120 об.
ТЕМА 5. МЕХАНИЧЕСКАЯ РАБОТА. МОЩНОСТЬ.
ЗАКОНЫ СОХРАНЕНИЯ ПРИ ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ
5.1 Закон сохранения импульса. Механическая работа, мощность, КПД.
Кинетическая и потенциальная энергия
Закон сохранения импульса
для замкнутой системы: 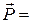  где n - число материальных точек (или тел), входящих в систему.
где n - число материальных точек (или тел), входящих в систему.
|
Элементарная работа, совершаемая постоянной силой: δA=  δA = Frdr = Fdrcos α,
где Fr -проекция силы на направление перемещения dr; α – угол между направлением силы и перемещения.
δA = Frdr = Fdrcos α,
где Fr -проекция силы на направление перемещения dr; α – угол между направлением силы и перемещения.
|
Работа, совершаемая переменной силой на пути: A =  Работа силы тяжести вблизи поверхности Земли: A =mgh;
Работа силы упругости: A =kx2/2.
Работа силы трения: A = - Ft Δr.
Мгновенная мощность:
Работа силы тяжести вблизи поверхности Земли: A =mgh;
Работа силы упругости: A =kx2/2.
Работа силы трения: A = - Ft Δr.
Мгновенная мощность:  N =Fv =Frv = Fvcos α
Коэффициент полезного действия (КПД): N =Fv =Frv = Fvcos α
Коэффициент полезного действия (КПД): 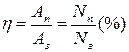 An, A3, Nn, N3 – соответственно полезные и затраченные работа и мощность
An, A3, Nn, N3 – соответственно полезные и затраченные работа и мощность
|
Кинетическая энергия: 
|
Связь между консервативной силой, действующей на тело в данной точке, и потенциальной энергией частицы:   = - grad Wп ;
Потенциальная энергия частицы в поле центральных сил:
Wп(r) = ΔA = - = - grad Wп ;
Потенциальная энергия частицы в поле центральных сил:
Wп(r) = ΔA = -  ,
предположив Wп(∞) = 0,
получим Wп(r) = ,
предположив Wп(∞) = 0,
получим Wп(r) =  .
Потенциальная энергия гравитационного взаимодействия двух материальных точек массами m1 и m2, находящихся на расстоянии r: .
Потенциальная энергия гравитационного взаимодействия двух материальных точек массами m1 и m2, находящихся на расстоянии r:  Потенциальная энергия тела в поле силы тяжести Земли:
Потенциальная энергия тела в поле силы тяжести Земли:  где r = R +h - расстояние от центра Земли до центра масс тела.
Потенциальная энергия тела в однородном поле силы тяжести (h<<R):
Wп = mgh, где g – ускорение свободного падения.
Потенциальная энергия упруго деформированного тела:
где r = R +h - расстояние от центра Земли до центра масс тела.
Потенциальная энергия тела в однородном поле силы тяжести (h<<R):
Wп = mgh, где g – ускорение свободного падения.
Потенциальная энергия упруго деформированного тела:  где k - коэффициент жесткости,
x – смещение;
σ – нормальное напряжение;
E – модуль Юнга;
V – объем.
где k - коэффициент жесткости,
x – смещение;
σ – нормальное напряжение;
E – модуль Юнга;
V – объем.
|
Пример 8.Автомобиль массой m = 2000 кг движется вверх по наклонной плоскости с уклоном α = 0,1, развивая на пути S = 100 м скорость vк = 36 км/ч. Коэффициент трения μ = 0,05. Найти среднюю и максимальную мощность двигателя автомобиля при разгоне.
 Условие:
Условие:
m =2000 кг;
S=100 м;
a=0,1 м/с2;
μ=0,05;
v0 =0;
vк =36км/ч = 10м/с;
Рср - ? Рmax - ?
Решение. Автомобиль движется равноускоренно, причем начальная скорость равна нулю. Выберем ось х, расположенную вдоль наклонной плоскости, ось у – перпендикулярно ей (рис. 3).
На автомобиль действует четыре силы: сила тяжести FТ=mg, сила реакции опоры N, сила тяги F и сила трения FТР. Запишем основной закон динамики:
 .
.
Это уравнение в проекциях на оси координат
на ось х ma = F – mg sina - FTP,
на ось у 0 = N – mg cosa,
FTP = μ N.
Выразим из этих уравнений силу тяги F
F = mg sina + μmg cosa + ma.
Ускорение на этом участке равно:
a = (vk 2 - v02)/(2s) = vk2/(2s).
Найдем силу тяги двигателя на этом участке:
F = mg sinα + μmgcosα +  = m(gsinα + μgcosα +
= m(gsinα + μgcosα +  )
)
Работа двигателя на этом участке: A = Fscosα,
где α – угол между F и s, равный нулю.
Подставив сюда выражение для F, получим
А = m(gsinα + μgcosα +  )s
)s
Средняя мощность равна PCP =  , где
, где 
 , откуда
, откуда

Максимальная мощность автомобиля достигается в тот момент, когда скорость максимальна: Pmax = F·vk,
Pср = 27·104 Вт, Pmax = 47·104 Вт.
Дата добавления: 2014-10-31; просмотров: 1747; Мы поможем в написании вашей работы!; Нарушение авторских прав |