
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. В магнитном поле на частицу действует сила Лоренца:
В магнитном поле на частицу действует сила Лоренца: 
Поскольку частица движется по окружности  , то сила Лоренца сообщает частице ускорение
, то сила Лоренца сообщает частице ускорение  . Следовательно
. Следовательно  (1)
(1)
Энергия частицы:  , следовательно
, следовательно 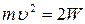 (2)
(2)
Подставляя (2) в (1), получим 
 ,
,
Из этого уравнения найдем заряд частицы: 
ТЕМА 12. РАБОТА В МАГНИТНОМ ПОЛЕ. ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ.
12.1. Поток вектора магнитной индукции (магнитный поток). Теорема Гаусса для поля 
Элементарный магнитный поток сквозь площадку dS:

|
Магнитный поток сквозь произвольную поверхность S

|
Магнитный поток в однородном поле:  где
где  - угол между направлением вектора нормали к площадки и вектора - угол между направлением вектора нормали к площадки и вектора  Единица измерения магнитного потока – 1 Вб (вебер) =1 Тл.м2
Единица измерения магнитного потока – 1 Вб (вебер) =1 Тл.м2
|
Теорема Гаусса для поля  :
Поток вектора магнитной индукции сквозь произвольную замкнутую поверхность равен нулю: :
Поток вектора магнитной индукции сквозь произвольную замкнутую поверхность равен нулю: 
|
12.2 Работа по перемещению проводника и контура с током в магнитном поле
Элементарная работа по перемещению проводника с током в магнитном поле: 
|
Работа по перемещению проводника с током в магнитном поле:

|
Работа по перемещению контура с током в магнитном поле
 где
где  - потокосцепление, N- число витков контура. - потокосцепление, N- число витков контура.
|
12.3. Закон Фарадея (закон электромагнитной индукции). Правило Ленца.
Закон Фарадея
ЭДС электромагнитной индукции в контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную контуром: 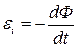
|
| Правило Ленца: Индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшему этот индукционный ток |
ЭДС индукции в неподвижных проводниках:  ,
где ,
где 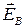 - напряженность электрического поля индуцированного переменным магнитным полем - напряженность электрического поля индуцированного переменным магнитным полем
|
ЭДС индукции в проводнике длиной l, движущемся в однородном магнитном поле c постоянной скоростью 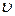 : :  ,
где ,
где  - угол между векторами - угол между векторами 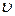 и и 
|
ЭДС индукции, возникающая при вращении рамки в магнитном поле – модель генератора: 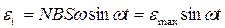 где N и S– число витков и площадь рамки,
В – индукция магнитного поля,
где N и S– число витков и площадь рамки,
В – индукция магнитного поля,  - угловая скорость вращения рамки, - угловая скорость вращения рамки, 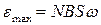 - максимальное значение ЭДС - максимальное значение ЭДС
|
12.4. Индуктивность контура. Самоиндукция.
Сцепленный с контуром магнитный поток
 ,
где коэффициент пропорциональности L называется индуктивностью.
Единица индуктивности – Гн (генри) =1 Ом.с ,
где коэффициент пропорциональности L называется индуктивностью.
Единица индуктивности – Гн (генри) =1 Ом.с
|
ЭДС самоиндукции в контуре:  Если контур не деформируется и магнитная проницаемость среды не меняется, то L=const и ЭДС самоиндукции
Если контур не деформируется и магнитная проницаемость среды не меняется, то L=const и ЭДС самоиндукции

|
Индуктивность соленоида: 
|
12.5 Токи при размыкании и замыкании цепи
Экстраток, возникающий при размыкании цепи:  ,
где ,
где  - время релаксации, за которое сила тока уменьшается в е раз - время релаксации, за которое сила тока уменьшается в е раз
|
Экстраток при замыкании цепи:  .
где .
где  - установившийся ток (при - установившийся ток (при 
|
12.6. Взаимная индукция. Трансформатор
Взаимная индукция - явление возникновения ЭДС в одном из контуров при изменении силы тока в другом
Индуцируемая в контурах ЭДС

|
Взаимная индуктивность двух катушек, намотанных на тороидальный сердечник: 
|
Трансформатор – устройство для понижения или повышения напряжения переменного тока
Коэффициент трансформации:  k > 1 – трансформатор понижающий
k < 1 – трансформатор повышающий
Коэффициент полезного действия трансформатора:
k > 1 – трансформатор понижающий
k < 1 – трансформатор повышающий
Коэффициент полезного действия трансформатора: 
|
12.7. Энергия магнитного поля.
Энергия магнитного поля контура с током: 
|
Энергия магнитного поля соленоида
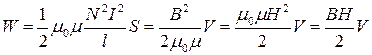 ,
где V=Sl – объем соленоида. ,
где V=Sl – объем соленоида.
|
Объемная плотность энергии магнитного поля:
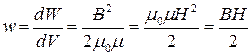
|
12.8 Магнитные свойства вещества. Магнетики
Орбитальный магнитный момент электрона
 ,
где I=e ,
где I=e  , ,  - частота вращения электрона по орбите, S – площадь орбиты, g – гиромагнитное отношение орбитальных моментов, е и m – заряд и масса электрона - частота вращения электрона по орбите, S – площадь орбиты, g – гиромагнитное отношение орбитальных моментов, е и m – заряд и масса электрона
|
Механический момент электрона: 
|
Собственный механический момент электрона (спин): 
|
Проекция  на направление вектора на направление вектора  может иметь одно из двух значений: может иметь одно из двух значений:  где
где  - магнетон Бора - магнетон Бора
|
Магнетик – вещество способное под действием магнитного поля приобретать магнитный момент (намагничиваться)
диамагнетики:  <1
парамагнетики: <1
парамагнетики:  > 1
ферромагнетики: > 1
ферромагнетики:  >> 1 >> 1
|
12.9 Закон полного тока для магнитного поля в веществе. Циркуляция вектора 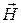
Теорема о циркуляции вектора  :
Циркуляция вектора магнитной индукции :
Циркуляция вектора магнитной индукции  : по произвольному замкнутому контуру равна алгебраической сумме токов проводимости и молекулярных токов, охватываемых этим контуром. умноженной на магнитную постоянную: : по произвольному замкнутому контуру равна алгебраической сумме токов проводимости и молекулярных токов, охватываемых этим контуром. умноженной на магнитную постоянную: 
|
Теорема о циркуляции вектора 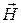 : :  , где , где 
|
12.10 Условия на границе раздела двух магнетиков
Вблизи границы раздела двух магнетиков:


|
12.11Основы теории Максвелла для электромагнитного поля
Изменяющееся во времени магнитное поле порождает электрическое поле ЕВ циркуляция которого 
|
Ток смещения:  Плотность тока смещения:
Плотность тока смещения:  .
где .
где  - вектор электрического смещения - вектор электрического смещения
|
Плотность тока смещения в диэлектрике:  ,
где ,
где  - плотность тока смещения в вакууме; - плотность тока смещения в вакууме;
 - плотность тока поляризации. - плотность тока поляризации.
|
Плотность полного тока: 
|
Обобщенная теорема о циркуляции вектора 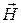 : :  
|
12.13 Уравнения Максвелла для электромагнитного поля
Полная система уравнений Максвелла в интегральной форме:
 
 ; ;  Величины, входящие в уравнение Максвелла, не являются независимыми и связаны так:
Величины, входящие в уравнение Максвелла, не являются независимыми и связаны так:

|
Полная система уравнений Максвелла в дифференциальной форме
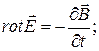 
 ; ; 
|
12.14 Следствия из уравнений Максвелла Свойства электромагнитных волн.
Волновое уравнение
  .
где .
где  - оператор Лапласа - оператор Лапласа
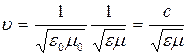 - фазовая скорость - фазовая скорость
  - скорость распространения электромагнитных волн в вакууме
Векторы - скорость распространения электромагнитных волн в вакууме
Векторы  колеблются в одинаковых фазах, причем: колеблются в одинаковых фазах, причем:

|
Объемная плотность энергии электромагнитных волн?

|
Вектор плотности потока энергии электромагнитной волны – вектор Пойнтинга: 
|
Пример 17.В однородном магнитном поле. индукция которого В =0.8 Тл. равномерно вращается рамка с угловой скоростью  =15 рад/с. Площадь рамки S = 150 см2. Ось вращения находится в плоскости рамки и составляет угол
=15 рад/с. Площадь рамки S = 150 см2. Ось вращения находится в плоскости рамки и составляет угол  =300 с направлением магнитного поля. Найти максимальную ЭДС индукции
=300 с направлением магнитного поля. Найти максимальную ЭДС индукции  во вращающейся рамке.
во вращающейся рамке.
Условие:
В = 0,8 Тл
 =15 рад/с
=15 рад/с
S= 150 cм2 =1,5.10-2 м2
 =300
=300
 -?
-?
Решение:
Мгновенное значение ЭДС индукции определяется законом Фарадея
 (1)
(1)
При вращении рамки магнитный поток, охватывающий рамку, изменяется по закону:
 (2)
(2)
подставив (2) в (1) и продифференцировав по времени, найдем мгновенное значение ЭДС индукции
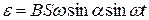
Максимальное значение ЭДС достигнет при  . Отсюда
. Отсюда
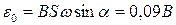
Дата добавления: 2014-10-31; просмотров: 384; Мы поможем в написании вашей работы!; Нарушение авторских прав |