КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ТЕМА 13. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫ
13.1 Механические колебания
Уравнение гармонических колебаний:
x = Acos (ω0t + φ); x = A sin (ω0t + φ),
где x –смещение колеблющейся величины от положения равновесия;
А – амплитуда колебаний;
ω=2πν =2π/T - угловая (циклическая) частота;
ν - частота колебаний; T - период; φ - начальная фаза.
Скорость и ускорение точки, совершающей гармонические колебания;
vx=  t = -Aω0sin (w0t + φ) = - Aω0cos (ωot + φ + π/2);
ax=  = - Aω2cos (ω0t + φ) = -ω02x
|
Динамическое уравнение гармонических колебаний:
 - kx или  , где ω02 = k/m
|
| Кинетическая энергия колеблющегося тела массой m: Wk =mv2/2 = mA2ω02sin2(ω0t + φ)/2. Потенциальная энергия: Wn= mA2ω02cos2(ω0t + φ)/2. Полная энергия: W = Wk + Wn = mA2ω02/2 = const |
Периоды колебания маятников:
пружинного: 
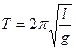математического:  ,
физического:  ,
где J- момент инерции маятника относительно оси колебаний;
l - расстояние между точкой подвеса и центром масс маятника;
L =J/ml - приведенная длина физического маятника;
g - ускорение свободного падения
|
Дифференциальное уравнение свободных затухающих колебаний линейной системы и его решение:  ; x = Ae-β tcos (ωt + φ),
где x – колеблющаяся величина, описывающая физический процесс;
β= r/2m - коэффициент затухания;
r –коэффициент сопротивления среды;
m - масса;
ω 0 –свободная циклическая частота незатухающих колебаний той же системы;
ω= (ω02- β2)1/2- частота затухающих колебаний;
Ae-β t - амплитуда затухающих колебаний.
|
| Декремент затухания: A(t)/A(t +T) = eβt, где A(t), A(t+T) - амплитуды двух последовательных колебаний соответствующих моментам времени, отличающимся на период. Логарифмический декремент затухания: θ=ln A(t)/ A(t+T) = β T = T/τ = 1/N, где τ – время релаксации N - число колебаний, совершаемых за время уменьшения колебаний в е раз. Добротность колебательной системы: Ω = π / θ = ω0/2β |
Дифференциальное уравнение вынужденных механических колебаний и его решение для установившихся колебаний:
x= Acos (Ωt - φ),
где x – координата колеблющейся точки;
F=F0cos Ωt – внешняя сила, вызывающая вынужденные колебания;
Амплитуда:  A = F0/ m [(ω02 - Ω2) + 4 β Ω2]1/2;
Фаза: φ=arctg 2βπ/(v02-Ω2)
Резонансная частота и резонансная амплитуда:
 ;
|
13.2. Упругие волны
| Связь длины волны λ, периода колебаний T и частоты ν: λ = vT = v/ ν; v = λν , где v –фазовая скорость (скорость распространения колебаний в среде) |
| Уравнение плоской волны, распространяющейся вдоль положительного направления оси х: x(t) = Acos (ωt – kx + φ0) где х(t) – координата точки в момент времени; A –амплитуда волны; ω - циклическая (круговая) частота; k = 2π/λ =2π/vT = ω/v – волновое число; λ – длина волны; v-фазовая скорость; T – период колебаний; φ0 – начальная фаза колебаний |
| Связь между разностью фаз Δφ и разностью хода d: Δφ= π d/ λ |
| Условия максимумов и минимумов амплитуды при интерференции: Δ φmax= ± 2πm; Δφmin= ± (2m+1)πm Δ dvax = ±m λ; Δ dmin= ± (2m+1) λ /2, где m = 0, 1, 2. |
| Фазовая v и групповая скорость u: v= ω/k; u =dω/dk; u = v - λ dv/dλ |
| Уравнение стоячей волны: x(t) = 2A(cos 2π x / λ)cosωt = 2Acoskx cos ωt. Координаты nучностей и узлов: xn = + m λ /2; xy = + (m +1/2)λ /2, m=0, 1, 2. |
Пример 17.Сплошной однородный диск колеблется около оси, перпендикулярной к плоскости диска и проходящей через край диска (рис.). Найти радиус диска, если приведенная длина этого физического маятника равна L = 0,15 м.
Условие:
L = 0,15 м;
R - ?
Решение. Период колебания физического маятника может быть рассчитан двояко: Тф = 2π(L/g)1/2, или Тф = 2π(J/mgd)1/2,
где J - момент инерции диска относительно оси вращения, проходящей через точку О; d – расстояние от оси вращения до центра тяжести, в данном случае d = R.
2π(L/g)1/2 = 2π(J/mgd)1/2 (1)
Из уравнения (1) находим: L = J/md.
По теореме Штейнера: J = J0 + md2,
где J0 –момент инерции относительно оси, параллельной оси вращения и проходящей через центр тяжести. Для диска J0 = mR2/2.
Итак, L = (J0 + md2)/md = 3R/2.
Откуда: R = 2L/3 = 0,10 м.
Пример 18.Определить возвращающую силу F в момент времени t = 0,2 c и полную энергию W точки массой m = 20 г, совершающей гармонические колебания согласно уравнению х = Asin ωt, где А =15 см; ω = 4 с-1. Найти также время t, когда х = А/2.
Решение. Силу по второму закону Ньютона определим как
F = ma, где ускорение а = d2x/dt2 = - Aω2sin ωt.
Тогда F = - mAω2sin ωt = -0,02 H.
Полная энергия колеблющейся точки равна W = mω2A2/2 = =3,55·10-2 Дж.
Время, через которое смещение х =А/2, найдем из того, что
А/2 = Аsin ωt, sin ωt = 1/2, ωt = π/6.
Откуда t = π/6ω = 4,17·10-2 c.
Дата добавления: 2014-10-31; просмотров: 232; Мы поможем в написании вашей работы!; Нарушение авторских прав |