
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сабақтың барысы. Таким образом, различие между атеистами и деистами эпохи Просвещения состоит в том, что Вольтеру и его единомышленникам указывает на присущее ей разумное
Таким образом, различие между атеистами и деистами эпохи Просвещения состоит в том, что Вольтеру и его единомышленникам указывает на присущее ей разумное, активное творящее начало, которое они называют «Богом», а атеисты приписывают эту активность, эту творческую мощь, наблюдаемую в мире, - самой природе (самой материи). Не стоит принижать природу, подчеркивает Ламетри[9]. Природа – создательница всего, что существует в мире как самого простого, так и самого сложного, именно ее творческая мощь есть причина существования всего, что существует.
И эту Природу (мир, как целое, Вселенную) мы можем понять, как некое живое существо. Уж точно, она не мертвая; если и механизм, то живой, иначе, откуда еще взяться активности и жизни.
Такое понимание природы мы найдем, в частности у Дидро в «Сне Д Аламбера». Природа, - пишет он, - ежечасно порождает и уничтожает множество своих творений. Этот бесконечный созидательный процесс Дидро сравнивает с брожением. Животные, мы, все окружающие вещи – промежуточные формы этого бесконечного процесса. Пройдет время и природа создаст какие-то иные формы (а старые уничтожит).
Вещи, согласно Дидро, являются промежуточными продуктами этого единого природного процесса. Это относится и к человеку. Носителем его индивидуальности, его «я» является (с точки зрения материалиста) не субстанция-душа (независимая, или, хотя бы, автономная), а память (вещь достаточно уязвимая). С исчезновением или повреждением памяти исчезнет и моя личность. Это и есть смерть.
Но жизнь вечна. Из того же самого материала, из которого природа сейчас слепила меня, она потом слепит еще что-то (тоже живое).
Мы боимся смерти, потому, что мы боимся потери памяти (потери своей собственной индивидуальности). Но если задуматься, мы умираем и при жизни: не только клеточки тела умирают и заменяются новыми, но и наша личность постепенно умирает, мы что-то забываем и обретаем новые воспоминания. Просто это процесс постепенный, - пишет Дидро, - поэтому мы его не боимся.
Таким образом, согласно материалисту Дидро, именно Вселенная, Природа является безусловным индивидом, личностью (самодостаточным целым), человеческая же личность является чем-то вторичным, небезусловным (временным образованием в потоке вселенской жизни).
__________________
Французский материализм 18-го века обычно называют «механистическим». Это и верно и неверно. С одной стороны он исходит из механицизма Декарта (из его понимания мира, как машины, и организма как машины). Но другой стороны «машина», о которой говорят французские материалисты – живая. Дидро и Ламетри стремятся вернуть миру то, что забрал у него Декарт (одушевленность).
«Мертвым» мир у Декарта оказывается потому, что он противопоставляет дух материи (и выносит дух (мыслящий разум) за пределы мира), материалисты же рассматривают духовное как свойство материального, сливая их воедино.
Ламетри пишет, что материализм – это исконное, древнейшее мировоззрение человека, и в этом он, несомненно, прав: человек изначально приписывал свойства духа тому, что он видит и ощущает (телам) (только зачем-то потом, с зарождением теоретической культуры стал делить то и другое).
Разделение духа и материи, понимание их как двух различных начал влечет за собой теоретические проблемы (что мы и видели у Декарта), интерпретация же духа как свойства материи может породить нечто вроде «материалистической мистики» (некое обожествление природы и уж точно поклонение перед ней). Это действительно напоминает мировоззрение человека дотеоретической культуры (впрочем, он был мудр).
[1] Именно на локковскую теорию познания: она представляет собой некую позицию здравого смысла. Беркли и Юм для просветителей чересчур эксцентричны. Берклианская религиозная философия им явно не подходит. Юма (похоже на то, что) современники вообще в очень малой степени восприняли. Возможно, первым кто действительно прочитал Юма, был Кант. Через него он и вошел в философскую традицию (но это было позже).
[2] «Имей мужество пользоваться собственным разумом» - так его формулирует Кант в работе «Что такое Просвещение?».
[3] «Деизм» - от латинского «Deus» - Бог. Слово образовано точно так же, как слово «теизм» («Theos» - «Бог» по-гречески). Слово «теизм» употребляется для более традиционного и ортодоксально христианского понимания Бога. «Деизм» Вольтера – специфически просвещенческий вариант не-атеизма.
[4] «Вольтер» - псевдоним. Философа звали Франсуа Мари Аруэ.
[5] Вольтер, Письма Меммия к Цицерону, глава 5.
[6] Смотри раздел «Физика Декарта».
[7] «Быть машиной, чувствовать, мыслить, уметь отличать добро от зла так же, как голубое от желтого, словом, родиться с разумом и устойчивым моральным инстинктом и быть только животным,— в этом заключается не больше противоречия, чем в том, что можно быть обезьяной или попугаем и уметь предаваться наслаждениям». Ламетри, «Человек-машина»
[8] Смотри, в частности: Дени Дидро, «Сон Д Аламбера».
[9]«В области природы мы — настоящие кроты. Мы движемся вперед точь-в-точь как это животное. Только наше высокомерие может стремиться ставить пределы тому, что их не имеет. Мы оказываемся в положении часов, которые могли бы сказать (вот хорошая тема для баснописца!): «Как, нас сделал глупый рабочий, нас, делящих на части время, точно отмечающих движение солнца и громко повторяющих указываемое нами время? Нет, этого быть не может!» Совершенно так же и мы, неблагодарные, отвергаем общую мать всех царств, по выражению химиков. Мы воображаем или, скорее, предполагаем существование причины более высокой, чем та, которой мы всем обязаны и которая действительно создала все непонятным для нас образом. Нет, в материи низменное существует только для грубых глаз, не познающих ее в самых блестящих ее творениях, и природу вовсе нельзя уподобить ограниченному рабочему. Она производит миллионы людей с гораздо большей легкостью и большей радостью, чем часовщик — самые сложные часы. Ее могущество одинаково проявляется в создании как самого ничтожного насекомого, так и самого гордого человека; живое царство стоит ей не большего труда, чем растительное, и самый великий гений — не более хлебного колоса…. Разбейте же цепь тяготеющих над вами предрассудков; вооружитесь факелом опыта, и вы окажете природе заслуженную ею честь, вместо того чтобы делать неблагоприятные для нее выводы на основании неведения, в котором она вас оставила» Ж. О. Ламетри «Человек-машина».
ФНП
$$$ 1
Градиент скалярного поля  имеет модуль:
имеет модуль:
$$$ 2
Если  – предел функции
– предел функции  в точке
в точке  , то
, то 
$$$ 3
Вычислить 
$$$ 4
Линией уровня функции  называется множество таких точек
называется множество таких точек  , для которых функция
, для которых функция 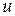 принимает:
принимает:
$$$ 5
Градиентом функции  в данной точке
в данной точке  называется вектор, координаты которого равны соответственно
называется вектор, координаты которого равны соответственно
$$$ 6
Физический смысл градиента градиент функции  указывает направление
указывает направление
$$$ 7
Градиентом функции  в данной точке
в данной точке  является вектор, координаты которого равны
является вектор, координаты которого равны
$$$ 8
Градиентом функции  в данной точке
в данной точке  является вектор, координаты которого равны
является вектор, координаты которого равны
$$$ 9
Градиентом функции 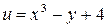 в данной точке
в данной точке  является вектор, координаты которого равны
является вектор, координаты которого равны
$$$ 10
Точками возможного экстремума функции 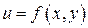 являются точки, в которых частные производные удовлетворяют условию:
являются точки, в которых частные производные удовлетворяют условию:
$$$ 11
Частное приращение функции 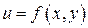 по переменной
по переменной  в точке
в точке  равно:
равно:
$$$ 12
Частной производной функции 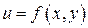 по
по  в точке
в точке  называется
называется
$$$ 13
Частная производная функции 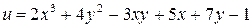 по
по  равна
равна
$$$ 14
Частная производная функции 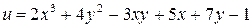 по
по  равна
равна
$$$ 15
Значение частной производной функции  по
по  в точке
в точке 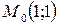 равно:
равно:
$$$ 16
Значение частной производной функции 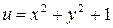 по
по  в точке
в точке 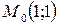 равно:
равно:
$$$ 17
Значение частной производной функции  по
по  в точке
в точке 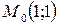 равно:
равно:
$$$ 18
Значение частной производной функции 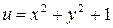 по
по  в точке
в точке 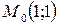 равно:
равно:
$$$ 19
Значение частной производной второго порядка  функции
функции 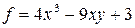 в точке
в точке 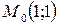 равно:
равно:
$$$ 20
Значение частной производной второго порядка  функции
функции
 в точке
в точке 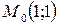 равно:
равно:
$$$ 21
Значение частной производной второго порядка 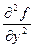 функции
функции 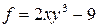 в точке
в точке 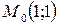 равно:
равно:
$$$ 22
Значение смешанной производной второго порядка 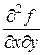 функции
функции 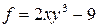 в точке
в точке 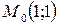 равно:
равно:
$$$ 23
Значение смешанной производной второго порядка  функции
функции  в точке
в точке 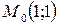 равно:
равно:
$$$ 24
Значение смешанной производной второго порядка  функции
функции  в точке
в точке 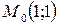 равно:
равно:
$$$ 25
Областью определения функции 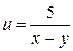 является множество точек, удовлетворяющих условию:
является множество точек, удовлетворяющих условию:
$$$ 26
Областью определения функции  является множество точек, удовлетворяющих условию:
является множество точек, удовлетворяющих условию:
$$$ 27
Областью определения функции  является множество точек, удовлетворяющих условию:
является множество точек, удовлетворяющих условию:
$$$ 28
Частное приращение функции  по
по  равно:
равно:
$$$ 29
Частное приращение функции 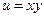 по
по 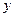 равно:
равно:
$$$ 30
Частное приращение функции  по
по 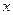 равно:
равно:
$$$ 31
Полным дифференциалом  функции
функции  , имеющий непрерывные частные производные, называется выражение:
, имеющий непрерывные частные производные, называется выражение:
$$$ 32
Полным дифференциалом  функции
функции  является выражение:
является выражение:
$$$ 33
Полным дифференциалом  функции
функции 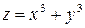 является выражение:
является выражение:
$$$ 34
Полным дифференциалом  функции
функции  является выражение:
является выражение:
$$$ 35
Производная  неявной функции
неявной функции  при условии
при условии 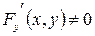 , равна:
, равна:
$$$ 36
Частная производная функции  по переменной
по переменной 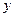
$$$ 37
Частная производная функции  по переменной
по переменной 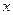
$$$ 38
Частная производная функции 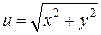 по переменной
по переменной 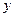
$$$ 39
Уравнение касательной плоскости в точке  к поверхности
к поверхности  имеет вид:
имеет вид:
$$$ 40
Уравнение нормали в точке  к поверхности
к поверхности  имеет вид:
имеет вид:
$$$ 41
Уравнение касательной плоскости в точке  к поверхности
к поверхности  имеет вид:
имеет вид:
$$$ 42
Уравнение касательной плоскости в точке  к поверхности
к поверхности
 имеет вид:
имеет вид:
$$$ 43
Достаточным условием локального экстремума функции  в точке М (необходимое условие экстремума выполняется) является следующее условие:
в точке М (необходимое условие экстремума выполняется) является следующее условие:
$$$ 44
Полный дифференциал функции 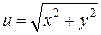 равен
равен
$$$ 45
Полный дифференциал функции  равен
равен
$$$ 46
Полный дифференциал функции  равен
равен
$$$ 47
Полный дифференциал функции  равен
равен
$$$ 48
Найти экстремум функции 
$$$ 49
Необходимым условием локального экстремума функции  в точке М является:
в точке М является:
$$$ 50
Найти экстремум функции 
$$$ 51
Какая формула соответствует понятию полного приращения функции двух переменных:
$$$ 52
Какая формула соответствует понятию частного приращения функции двух переменных по 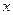 :
:
$$$ 53
Какая формула соответствует понятию частного приращения функции двух переменных по 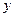 :
:
$$$ 54
Среди представленных ниже формул найдите формулу для вычисления градиента функции двух переменных:
$$$ 55
Найти экстремум функции 
$$$ 56
Частный дифференциал функции  по
по 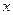 равен:
равен:
$$$ 57
Частный дифференциал функции  по
по 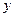 равен:
равен:
$$$ 58
Градиентом функции  в точке
в точке  является:
является:
$$$ 59
Если точка  – точка возможного экстремума дважды дифференцируемой функции
– точка возможного экстремума дважды дифференцируемой функции  , то она является точкой максимума при условиях:
, то она является точкой максимума при условиях:
$$$ 60
Если точка  – точка возможного экстремума дважды дифференцируемой функции
– точка возможного экстремума дважды дифференцируемой функции  , то она является точкой минимума при условиях:
, то она является точкой минимума при условиях:
$$$ 61
Точками возможного экстремума или стационарными функции 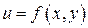 являются точки, в которых:
являются точки, в которых:
$$$ 62
Частная производная  функции
функции 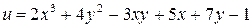 равна:
равна:
$$$ 63
Значение частной производной  функции
функции 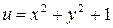 в точке
в точке 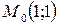 равно:
равно:
$$$ 64
Найти точки экстремума функции 
$$$ 65
Найти производную неявно заданной функции  в точке (4,0):
в точке (4,0):
$$$ 66
Найти производную неявно заданной функции 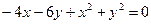 в точке (0,-1):
в точке (0,-1):
$$$ 67
Найти производную неявно заданной функции  в точке (8,1):
в точке (8,1):
$$$ 68
В точке стационарной  – дважды дифференцируемой функции
– дважды дифференцируемой функции  нет экстремума, если:
нет экстремума, если:
$$$ 69
Найти точки экстремума функции 
$$$ 70
Найти точки экстремума функции 
$$$ 71
Найти экстремум функции 
$$$ 72
Дифференциальное уравнение первого порядка  называется
называется
$$$ 73
Дифференциальное уравнение вида  ,
,  ,
,  называется
называется 
$$$ 74
Дифференциальное уравнение  или
или 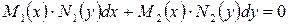 называется
называется
$$$ 75
Дифференциальное уравнение первого порядка  называется
называется
$$$ 76
Если  , то дифференциальное уравнение
, то дифференциальное уравнение 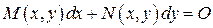 называется
называется
$$$ 77
Дифференциальное уравнение второго порядка 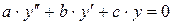 называется
называется
$$$ 78
Дифференциальное уравнение второго порядка 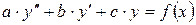 называется
называется
$$$ 79
Укажите замену, приводящую уравнение Бернулли  ,
,  ,
,  к линейному уравнению первого порядка
к линейному уравнению первого порядка
$$$ 80
Укажите общее решение дифференциального уравнения  , где
, где 
$$$ 81
Укажите общее решение дифференциального уравнения  , где
, где 
$$$ 82
Укажите характеристическое уравнение для линейного однородного дифференциального уравнения с постоянными коэффициентами 
$$$ 83
С помощью какой замены понижается порядок дифференциального уравнения вида 
$$$ 84
С помощью какой замены понижается порядок дифференциального уравнения вида 
$$$ 85
С помощью какой замены понижается порядок дифференциального уравнения вида 
$$$ 86
Если функции 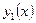 и
и  линейно независимые на
линейно независимые на  то для любого
то для любого 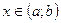 определитель Вронского
определитель Вронского  удовлетворяет условию
удовлетворяет условию 
$$ 87
Если функции 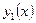 и
и  на
на  линейно зависимые, то для любого
линейно зависимые, то для любого 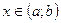 определитель Вронского
определитель Вронского  удовлетворяет условию
удовлетворяет условию 
$$$ 88
Общее решение дифференциального уравнения  где
где  имеет вид
имеет вид
$$$ 89
Укажите общее решение дифференциального уравнения 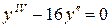
$$$ 90
Укажите общее решение дифференциального уравнения 
$$$ 91
Укажите характерическое уравнение дифференциального уравнения 
$$$ 92
Решить уравнения 
$$$ 93
Решить уравнения 
$$$ 94
Решить уравнения 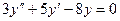
$$$ 95
Решить уравнение 
$$$ 96
Решить уравнение 
$$$ 97
Решить уравнение 
$$$ 98
Решить уравнение 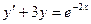
$$$ 99
Решить уравнение 
$$$ 100
Решить уравнение 
$$$ 101
Решить уравнение 
$$$ 102
Решить уравнение 
$$$ 103
Решить уравнение 
$$$ 104
Решить уравнение 
$$$ 105
Решить уравнение 
$$$ 106
Решить уравнение 
$$$ 107
Решить уравнение 
$$$ 108
Решить задачу Коши  ,
, 
$$$ 109
Решить задачу Коши 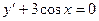 ,
, 
$$$ 110
Решить задачу Коши  ,
, 
$$$ 111
Решить задачу Коши  ,
,  ,
, 
$$$ 112
Если в 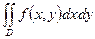 произвести замену переменных:
произвести замену переменных: 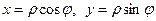 , то якобиан
, то якобиан
равен:
$$$ 113
Тройной интеграл  равен
равен
$$$ 114
Двойной интеграл  равен
равен
$$$ 115
Если непрерывная в области  функция
функция  , то двойной интеграл
, то двойной интеграл  выражает
выражает
$$$ 116
Переход из прямоугольных координат 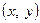 к полярных координат
к полярных координат  осуществляется равенствами:
осуществляется равенствами:
$$$ 117
В интеграле  при переходе к полярным координатам, используются формулы:
при переходе к полярным координатам, используются формулы:
$$$ 118
В интеграле  при переходе к цилиндрическим координатам, используются формулы:
при переходе к цилиндрическим координатам, используются формулы:
$$$ 119
Масса однородной пластинки  выражается формулой
выражается формулой
$$$ 120
Изменить порядок интегрирования в повторном интеграле: 
$$$ 121
Изменить порядок интегрирования в повторном интеграле: 
$$$ 122
Изменить порядок интегрирования в повторном интеграле: 
$$$ 123
Изменить порядок интегрирования в повторном интеграле: 
$$$ 124
Изменить порядок интегрирования в повторном интеграле: 
$$$ 125
Вычислить двойной интеграл  , где
, где 
$$$ 126
Вычислить двойной интеграл  , где
, где 
$$$ 127
Вычислить двойной интеграл  , где
, где 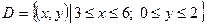
$$$ 128
Вычислить двойной интеграл  , где
, где 
$$$ 129
Вычислить двойной интеграл  , где
, где 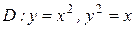 :
:
$$$ 130
Вычислить двойной интеграл  , где
, где  :
:
$$$ 131
Вычислить площадь  , ограниченной линиями:
, ограниченной линиями:  ,
,  ,
, 
$$$ 132
Вычислить площадь  , ограниченной заданным линиями:
, ограниченной заданным линиями:  ,
, 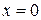 ,
, 
$$$ 133
Вычислить площадь  , ограниченной заданным линиями:
, ограниченной заданным линиями:  ,
,  ,
, 
$$$ 134
Изменить порядок интегрирования в двойном интеграле  :
:
$$$ 135
Расставить пределы интегрирования в тройном интеграле  ,
,
 ,
,  ,
,  ,
,  ,
,  :
:
$$$ 136
Расставить пределы интегрирования в тройном интеграле  , где
, где  ,
,  ,
, 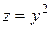 ,
,  :
:
$$$ 137
Расставить пределы интегрирования в тройном интеграле  , где
, где  ,
,  ,
,  ,
,  ,
,  :
:
$$$ 138
Вычислить интеграл: 
$$$ 139
Вычислить интеграл: 
$$$ 140
Вычислить интеграл: 
$$$ 141
Вычислить интеграл: 
$$$ 142
Найти площадь области  , ограниченной линиями
, ограниченной линиями  ,
,  :
:
$$$ 143
Найти площадь области  , ограниченной линиями
, ограниченной линиями 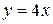 ,
, 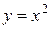 :
:
$$$ 144
Найти площадь области  , ограниченной линиями
, ограниченной линиями  ,
, 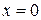 ,
,  ,
,  :
:
$$$ 145
Вычислить интеграл: 
$$$ 146
Вычислить интеграл: 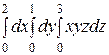
$$$ 147
Вычислить интеграл: 
$$$ 148
Вычислить интеграл: 
$$$ 149
Вычислить интеграл: 
$$$ 150
Вычислить интеграл: 
$$$ 151
Вычислить интеграл: 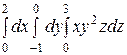
$$$ 152
Вычислить интеграл: 
$$$ 153
Вычислить интеграл: 
$$$ 154
Вычислить интеграл: 
$$$ 155
Вычислить интеграл: 
$$$ 156
Укажите необходимое условие сходимости числового ряда 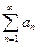
$$$ 157
Укажите достаточное условие расходимости числового ряда 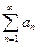
$$$ 158
При каких значениях параметра  , ряд
, ряд  сходится
сходится
$$$ 159
Укажите радикальный признак сходимости Коши числового ряда 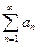
$$$ 160
Исследовать на сходимость ряд 
$$$ 161
Укажите признак сходимости Даламбера числового ряда
$$$ 162
Укажите условие сходимости знакочередующего ряда 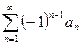
$$$ 163
Укажите радиус сходимости степенного ряда 
$$$ 164
Укажите разложение в ряд Маклорена функции 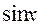
$$$ 165
Укажите разложение в ряд Маклорена функции 
$$$ 166
Укажите разложение в ряд Маклорена функции 
$$$ 167
Укажите ряд Тейлор функции  в точке
в точке 
$$$ 168
Укажите функциональный ряд
$$$ 169
Найти сумму ряда 
$$$ 170
Если для числовых рядов  и
и 
 выполняется неравенство
выполняется неравенство  , то
, то
$$$ 171
Найдите область сходимости ряда 
$$$ 172
Укажите для числового ряда  правильную формулировку
правильную формулировку
$$$ 173
Чему равен радиус сходимости степенного ряда  , если
, если 
$$$ 174
Если степенной ряд 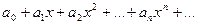 сходится, в точке
сходится, в точке  , то
, то
$$$ 175
Если степенной ряд 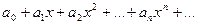 расходится в точке
расходится в точке  , то
, то
$$$ 176
Определением условной сходимости знакопеременного ряда  является
является
$$$ 177
Найти сумму ряда 
$$$ 178
Исследовать на сходимость ряд 
$$$ 179
Найти область сходимости ряда 
$$$ 180
Найти область сходимости ряда 
$$$ 181
Найти радиус сходимости ряда 
$$$ 182
Найти радиус сходимости ряда 
$$$ 183
Найти область сходимости ряда 
$$$ 184
Найти область сходимости ряда 
$$$ 185
Найти сумму ряда 
$$$ 186
Найти сумму ряда 
$$$ 187
Исследовать на сходимость ряд 
$$$ 188
Исследовать на сходимость ряд 
$$$ 189
Исследовать сходимость ряда 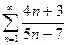
$$$ 190
Исследовать сходимость ряда 
$$$ 191
Исследовать на сходимость ряд 
$$$ 192
Исследовать сходимость ряда 
$$$ 193
Исследовать сходимость ряда 
$$$ 194
Найти общий член ряда 
$$$ 195
Исследовать на сходимость ряд 
$$$ 196
Исследовать на сходимость ряд 
$$$ 197
Найти радиус сходимости ряда 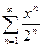
$$$ 198
Исследовать на сходимость ряд 
$$$ 199
Найти общий член ряда 
$$$ 200
Исследовать на сходимость ряд 
$$$ 201
Найти интервал сходимости ряда 
$$$ 202
Найти интервал сходимости ряда 
$$$ 203
Найти радиус сходимости ряда 
$$$ 204
Найти радиус сходимости ряда 
$$$ 205
Найти 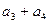 для ряда
для ряда 
$$$ 206
Исследовать на сходимость ряд 
$$$ 207
Найти интервал сходимости ряда 
$$$ 208
Ряд 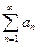 называется сходящимся, если
называется сходящимся, если
$$$ 209
Найти интервал сходимости ряда 
$$$ 210
Найти интервал сходимости ряда 
$$$ 211
Найти область сходимости ряда 
$$$ 212
Найти область сходимости ряда 
$$$ 213
Найти интервал сходимости ряда 
$$$ 214
Найти интервал сходимости ряда 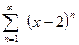
$$$ 215
 в точке
в точке  расходится, что можно сказать о сходимости ряда в точке
расходится, что можно сказать о сходимости ряда в точке 
$$$ 216
 в точке
в точке  расходится, что можно сказать о сходимости ряда в точке
расходится, что можно сказать о сходимости ряда в точке 
$$$ 217
Найдите общий член ряда 
$$$ 218
Если ряд  сходится, то ряд
сходится, то ряд  ?
?
$$$ 219
Если ряд  и
и  сходятся, то
сходятся, то 
$$$ 220
Если ряд  сходится в точке
сходится в точке 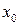 то он
то он
Сабақтың барысы
| Сабақтың кезеңде-рі | Мұғалімнің іс-әрекеті | Оқушылардың іс-әрекеті |
| 1.Ұйымдасты-ру кезеңі (3 мин) | Оқушылармен амандасу. Түгендеу. Сабаққа дайындығын тексеру. Психологиялық дайындығын тексеру. | Орындарынан тұрып мұғаліммен амандасу. Сабақта кім жоқ екенін анықтау. Сабаққа дайындалу. |
| 2. Білім мен іс-керліктерін жан-жақты тексеру кезеңі. (10+1-2 мин) | Оқушыларға өткен тақырып бойынша сұрақтар қою арқылы білімдерін тексереді. 1. «Алашорда» үкіметінің құрылуы 2. Қазақстан аумағында құрылған саяси партиялардың қызметі мақсаттары туралы 3. Жетекшілері | Оқушылар сұрақтарға жауап береді: |
| 3.Жаңа материалға көшу кезеңі | Тақырып мазмұнымен таныстыру. Кіріспенің сызбанұсқасын талдау, біртіндеп кіріспеге көшу. «ББҮ» стратегиясы бойынша оқушылар ойларын анықтау | Тақырып мазмұнымен танысады. Кіріспенің сызбанұсқасын мүғаліммен талдап, кіріспеге көшеді. |
| 4. Жаңа материалды меңгерту кезеңі. | 1. Қазақстанда Кеңес билігінің орнауы. 1-топ 2. Большевиктердің алғашқы шаралары. 2-топ 3. Ұлт мәселелерінің қойылуы, әлеуметтік-экономикалық мәселелердің қойылуы. 3-топ | |
| 5. Жаңа тақырыпты бекіту кезеңі | ||
| 6. Сабақты қорытындылау кезеңі | ||
| 7. Бағалау кезеңі | Оқушыларды сабаққа қатысуына қарай бағалайды. | |
| 8. Үйге тапсырма беру кезеңі |
Сабақ №2
Күні:
Сынып: 9
Тақырыбы: Экономикалық географиялық жағдайы және табиғи ресурстық әлует
Мақсаттары:
Білімділік. Қазақстанның дүние жүзі картасында алатын орнын, экономикалық-географиялық жағдайын, оның артықшылықтары мен кемшіліктерін анықтап, табиғи ресурстық әлеуетін сипаттауға бағдар беру. Қазақстанның әкімшілік-аумақтық бөлінісін анықтау.
Дамытушылық.Қазақстанның географиялық орнын және табиғи ресурстық әлеуетін карта бойынша сипаттау арқылы білімдерін тереңдету.
Тәрбиелік. Өз отаны туралы білімдерін тереңдете келе, отансүйгіштік қасиеттерін артыру, географиялық мәдениетке тарту.
Сабақ түрі: жаңа тақырып
Сабақты үйымдастыру формасы: фронтальді
Сабақты жүргізу әдіс-тәсілдері: сұрақ-жауап
Құрал-жабдықтар: Дүние жүзінің саяси картасы, Қазақстанның саяси картасы
Негізгі ұғымдар: географиялық орын, әкімшілік-аумақтық құрылым, облыс, аудан, округ, экономикалық-географиялық жағдай, табиғи-ресурстық әлеует, табиғи жағдай, табиғи ресурстардың аумақтық үйлесімі
Номенклатура: Семей, Ақтөбе, Қарағанды, Астана, Алматы, Ақтау, Шымкент
Дата добавления: 2015-01-05; просмотров: 282; Мы поможем в написании вашей работы!; Нарушение авторских прав |