
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Поляризация света при отражении и преломлениина границе раздела
С чем связано наличие собственного языка логики как науки?
Естественному языку присущи некоторые недостатки, которые не позволяют логике пользоваться только им. Основными недостатками
естественного языка являются:
• изменение значения слов с развитием общественной практики и по истечении определенного времени;
• многозначность некоторых слов;
• расплывчатость, неопределенность отдельных слов, не позволяющая с их помощью определить предмет науки;
• несовершенство правил построения выражений, которое в логическом смысле несет на себе печать многозначности понимания вер-
бальной мысли;
• деление естественного языка на большое количество языков разных стран и народов, в результате чего одна и та же мысль может бытьоформлена различными языками.
Бытует мнение, что в естественных языках можно сформулировать все то, что фиксируется специальными средствами в искусственных
языках. Предполагается, что все отличие искусственных языков от естественных состоит лишь в замене слов и выражений специаль-
ными символами. Этим достигается определенный эффект краткости,сжатости сообщений, как бы их некоторая стенограмма. Такое понимание роли искусственных языков не является верным.
науки логики этап развития логики (XIX – нач. ХХ в.) связан с разработкой применительно к анализу мышления точных матема-
тических методов и построением искусственных символических языков. Этот этап отмечен именами Д. Буля, О. де Моргана, Г. Фреге,Б. Рассела и знаменует собой переход к современной, символической логике. Широкое использование в ней символических языков и ориентация на обоснование математического знания породили еще одно название современной логики – математическая логика.
Искусственные языки вводятся как инструмент эффективного представления определенных связей и отношений. Цель использова-
ния искусственных языков в логике – не замена слов естественного языка некоторыми специальными символами, а воспроизведение
логической дедукции. Поэтому логические системы строятся часто в ущерб «краткости и легкости общения». Сложные рассуждения
практически невозможно «перевести» с искусственного языка на естественный, без утраты их эффективного и доказательного характера.
Кроме того, построение специальных языков логики позволяет конструировать новые способы рассуждения.
Язык – это знаковая система, предназначенная для фиксации,хранения, переработки и передачи информации.
Различают естественные языки (русский, китайский, английский и т. д.), возникшие стихийно как средство общения между людьми,
и искусственные (эсперанто, языки программирования, логические языки и т. д.) – сознательно созданные человеком для решения определенных задач
Всякий язык состоит из знаков.Знак – это материальный объект, для некоторого интерпретатора выступающий в качестве представителя какого-то предмета.
Предмет в данном случае трактуется широко – как любой материальный или идеальный объект, на который направлена наша мысль.
Предмет составляет значение знака. Интерпретатор – это человек, способный осмысленно употреблять данные знаки. В качестве
интерпретатора может выступать и отдельная группа людей (например, молодежь как носитель определенного «молодежного» языка),
и научное сообщество, и, в конечном счете, человечество в целом.
значение интерпретатор
В семиотике выделяется три раздела: синтаксис, семантика и прагматика. Синтаксис изучает отношения между знаками, т.е. правила
построения языка. Отношение знаков к обозначаемым ими объектами ситуациям (т. е. знака к значению) является предметом семантики.Прагматика занимается проблемами понимания и интерпретации знаков людьми – носителями языка, а также отношениями, возникающими между людьми в процессе знакового общения.
В логической семантике помимо понятий знак и значение вводится также понятие смысл знака. Смысл – это способ указания на объект,
Символы традиционной логики
S – символ для обозначения субъекта простого атрибутивного суждения (предмета мысли, логического подлежащего), а также обозна-
чение субъекта – меньшего термина силлогизма.
P – символ предиката простого атрибутивного суждения (логического сказуемого), а также обозначение предиката – большего тер-
мина силлогизма.
М – средний термин силлогизма.«Есть» – «не есть» («суть» – «не суть» и пр.) – логическая связка
между субъектом и предикатом простого атрибутивного суждения.
R – символ любого отношения.
А – символ общеутвердительного суждения.
Е – символ общеотрицательного суждения.
I – символ частноутвердительного суждения.
О – символ частноотрицательного суждения.

52.Основные формы теоретического знания
Основные формы теоретического знания:научная проблема, гипотеза,теория ,принципы, категория,
В современной юридической практике широко используется весь богатейший арсенал логических средств:
• определение (юридических понятий),
• деление (например, классификация преступлений),
• подведение под понятие (например, квалификация конкретного
деяния),
• версия как вид гипотезы (следственная версия),
• умозаключение (например, в обвинительном заключении),
• доказательство и опровержение (например, во время судебного
разбирательства) и т. д.
Поляризация света при отражении и преломлениина границе раздела
двух диэлектрических сред. Закон Брюстера. @
Действие поляризаторов может быть основано на поляризации света при отражении и преломлении на границе раздела двух диэлектриков.
Оптически изотропная среда (т.е. среда, имеющая одинаковые оптические свойства во всех направлениях) представляет собой систему электрических зарядов – ионов и электронов, способных совершать вынужденные колебания под действием электромагнитных волн. Частота колебаний, соответствующая диапазону частот видимого света очень большая (порядка 1015 Гц). Поэтому только заряженные частицы очень маленькой массы могут следовать за изменением поля световой волны. Такими частицами являются электроны. Атомы и их ядра не могут следовать за изменением этого поля в силу их большой инертной массы. При этом предполагается, что в веществе электроны связаны квазиупругими силами, т.е. являются колебательными системами, характеризующимися частотой собственных колебаний.
 Простейшей системой, излучающей электромагнитные волны, является колеблющийся электрический диполь (рис. 4.4 а). Под действием электромагнитной волны электроны вещества совершают вынужденные колебания, излучая вторичные электромагнитные волны той же частоты, что и частота падающего света. Если волна распространяется в изотропной среде, то волновой фронт будет сферическим (рис. 4.4 б). При этом интенсивность вторичных волн зависит от угла θ и поэтому различна в разных направлениях. Зависимость интенсивности от угла наглядно показано на диаграмме направленности диполя (рис. 4.4 в). На рис. 4.4.в видно, что в направлении линии АА' (оси осциллятора) происходит колебания электрона, поэтому интенсивность излучения в этом направлении отсутствует. Интенсивность излучения будет максимальна в направлении оси Х, перпендикулярном линии АА'.
Простейшей системой, излучающей электромагнитные волны, является колеблющийся электрический диполь (рис. 4.4 а). Под действием электромагнитной волны электроны вещества совершают вынужденные колебания, излучая вторичные электромагнитные волны той же частоты, что и частота падающего света. Если волна распространяется в изотропной среде, то волновой фронт будет сферическим (рис. 4.4 б). При этом интенсивность вторичных волн зависит от угла θ и поэтому различна в разных направлениях. Зависимость интенсивности от угла наглядно показано на диаграмме направленности диполя (рис. 4.4 в). На рис. 4.4.в видно, что в направлении линии АА' (оси осциллятора) происходит колебания электрона, поэтому интенсивность излучения в этом направлении отсутствует. Интенсивность излучения будет максимальна в направлении оси Х, перпендикулярном линии АА'.
 Взаимодействие электронной оболочки атомов с электромагнитным полем световой волны приводит к их возбуждению. Возбужденные атомы, приходя в нормальное (невозбужденное) состояние, излучают вторичные электромагнитные волны. Поскольку среднее расстояние между атомами в жидкостях и твердых телах мало по сравнению с длиной цуга волн (около 3м), то электронные оболочки большого числа атомов возбуждаются одним цугом волн. Поэтому вторичные волны оказываются когерентными как между собой, так и падающей световой волной. Эти волны взаимно интерферируют. Их интерференцией объясняются явления отражения и преломления света в веществе.
Взаимодействие электронной оболочки атомов с электромагнитным полем световой волны приводит к их возбуждению. Возбужденные атомы, приходя в нормальное (невозбужденное) состояние, излучают вторичные электромагнитные волны. Поскольку среднее расстояние между атомами в жидкостях и твердых телах мало по сравнению с длиной цуга волн (около 3м), то электронные оболочки большого числа атомов возбуждаются одним цугом волн. Поэтому вторичные волны оказываются когерентными как между собой, так и падающей световой волной. Эти волны взаимно интерферируют. Их интерференцией объясняются явления отражения и преломления света в веществе.
При падении естественного света на границу раздела двух диэлектриков (например, из воздух на стекло) часть его отражается, а часть преломляется (рис. 4.5). Отраженный и преломленный свет оказываются частично поляризоваными. В отраженном свете преобладают волны, у которых световой вектор Е колеблется в плоскости, перпендикулярной плоскости падения (на рис. 4.5 колебания вектора Е изображены точками), а в преломленном свете – в плоскости падения (на рис. 4.5 колебания вектора Е изображены стрелками).
Степень поляризации как отраженного, так и преломленного света зависит от угла падения лучей и показателей преломления сред. Шотландский физик Дэвид Брюстер исследуяполяризацию света, установил (1815 г.) связь между относительным показателем преломления диэлектрика и углом падения света, при котором отраженный от поверхности свет полностью поляризован. Согласно закону Брюстера при угле падения iБ (угол Брюстера), определяемого соотношением
 tg iБ = n21
tg iБ = n21
отраженный луч будет полностью плоскополяризован а преломленный луч – частично с максимальной степенью поляризации (рис. 4.6). Если свет падает на границу раздела под углом Брюстера, то отраженный и преломленный лучи взаимно перпендикулярны (это условие вытекает из закона Брюстера).
Степень поляризации преломленного света можно значительно повысить, пропуская свет через устройство, называемое стопой Столетова (рис. 4.7). Стопа Столетова представляет собой совокупность одинаковых параллельных друг другу пластинок из прозрачного диэлектрика (например, стекла). При многократном отражении и преломлении на каждой границе степень поляризации вырастает и на выходе из стопы свет становится полностью поляризованным.
 Закон Брюстера можно пояснить, основываясь на диаграмме направ
Закон Брюстера можно пояснить, основываясь на диаграмме направ  ленности излучения электрического диполя (осциллятора). Представим падающий естественный свет как результат сложения двух взаимно перпендикулярных колебаний (рис. 4.8). Один световой вектор (обозначим его Е||) будет колебаться в плоскости падения (на рис. 4.8 вектор Е|| показан стрелками), а другой (обозначим его Е^) будет колебаться в плоскости, перпендикулярной плоскости падения (на рис. 4.8 вектор Е^ показан точками).
ленности излучения электрического диполя (осциллятора). Представим падающий естественный свет как результат сложения двух взаимно перпендикулярных колебаний (рис. 4.8). Один световой вектор (обозначим его Е||) будет колебаться в плоскости падения (на рис. 4.8 вектор Е|| показан стрелками), а другой (обозначим его Е^) будет колебаться в плоскости, перпендикулярной плоскости падения (на рис. 4.8 вектор Е^ показан точками).
При прохождении света через вещество под действием вектора Е|| электроны вещества будут совершать вынужденные колебания в плоскости падения (эти осцилляторы, оси которых лежат в плоскости падения, на преломленном луче обозначены стрелками), излучая при этом вторичные сферические волны в плоскости падения. Интенсивность таких волн будет максимальна в перпендикулярном направлении (это показано диаграммой направленности диполя на преломленном луче). Световому векторуЕ^ будут соответствовать осцилляторы, оси которых лежат в перпендикулярной плоскости (на преломленном луче они обозначены точками). В направлении колебаний электронов излучения вторичных волн не происходит. При угле падения i = iБотраженный луч перпендикулярен преломленному лучу и, следовательно, параллелен осцилляторам, оси которых расположены в плоскости падения. Данные осцилляторы не излучают в направлении отраженного луча и вклад в отраженную волну не дают. Отсюда следует, что в отраженном луче будет присутствовать только колебания Е^ и отраженный луч будет полностью поляризован.
Эффект поляризации отраженного света используется, например, для обнаружения с воздуха пленок нефти на поверхности моря.
4. 3. Поляризация света при двойном лучепреломлении. @
Действие ряда поляризаторов основано на поляризации света при прохождении его через оптически анизотропные среды (т.е. среды, имеющие различные оптические свойства в различных направлениях). Все прозрачные кристаллы оптически анизотропны. Исключением являются кристаллы, имеющие кубическую кристаллическую решетку (например, соль NaCl). При прохождении света через оптически анизотропные кристаллы наблюдается явление двойного лучепреломления, которое состоит в том, что упавший на кристалл луч разделяется внутри кристалла на два луча, распространяющиеся с различными скоростями и в различных направлениях. Это явление впервые было обнаружено датским ученым Э. Бартолином в 1669 г. для исландского шпата.
В зависимости от типа симметрии оптически анизотропные кристаллы бывают одноосные либо двуосные, т.е. имеют одну или две оптические оси. Оптической осью называется такое направление в кристалле, вдоль которого распространяющийся свет не испытывает двойного лучепреломления. Важно отметить, что любая прямая параллельная данному направлению, также является оптической осью кристалла. Примером одноосного кристалла (рис. 4.9) является исландский шпат (диагональ кристалла ОО' совпадает с оптической осью), а также кварц, турмалин, апатит и другие. К двуосным кристаллам относятся гипс, слюда, топаз.
 В одноосных кристаллах (рис. 4.9 а) один из преломленных лучей, образующихся при двойном лучепреломлении, лежит в плоскости падения и подчиняется закону преломления, поэтому его назвалиобыкновенным лучом и обозначают буквой "о". Скорость обыкновенного луча υо численно одинакова по всем направлениям: υо = c/nо, где nо = const- показатель преломления кристалла для обыкновенного луча. Второй луч называют необыкновенным и обозначают буквой "е". Он не лежит в плоскости падения и не подчиняется закону преломления. Соответственно скорость необыкновенного луча υе = c/nе, где nе - показатель преломления кристалла для необыкновенного луча. Значения nе и υе зависят от направления распространения необыкновенного луча по отношению к оптической оси кристалла. Для луча, распространяющегося вдоль оптической оси показатели преломления обыкновенного и необыкновенного лучей равны nе = nо и υе = υо. Значение nе наиболее сильно отличается от nо для направления, перпендикулярного оптической оси. Все эти различия между обыкновенным и необыкновенным лучами имеют место только внутри кристалла. На выходе из кристалла оба луча распространяются с одинаковой скоростью. В двуосных кристаллах оба преломленных луча ведут себя как необыкновенные.
В одноосных кристаллах (рис. 4.9 а) один из преломленных лучей, образующихся при двойном лучепреломлении, лежит в плоскости падения и подчиняется закону преломления, поэтому его назвалиобыкновенным лучом и обозначают буквой "о". Скорость обыкновенного луча υо численно одинакова по всем направлениям: υо = c/nо, где nо = const- показатель преломления кристалла для обыкновенного луча. Второй луч называют необыкновенным и обозначают буквой "е". Он не лежит в плоскости падения и не подчиняется закону преломления. Соответственно скорость необыкновенного луча υе = c/nе, где nе - показатель преломления кристалла для необыкновенного луча. Значения nе и υе зависят от направления распространения необыкновенного луча по отношению к оптической оси кристалла. Для луча, распространяющегося вдоль оптической оси показатели преломления обыкновенного и необыкновенного лучей равны nе = nо и υе = υо. Значение nе наиболее сильно отличается от nо для направления, перпендикулярного оптической оси. Все эти различия между обыкновенным и необыкновенным лучами имеют место только внутри кристалла. На выходе из кристалла оба луча распространяются с одинаковой скоростью. В двуосных кристаллах оба преломленных луча ведут себя как необыкновенные.
Исследование обыкновенного и необыкновенного лучей показывает, что оба луча на выходе из кристалла полностью поляризованы. Вектор Е обыкновенного луча колеблется перпендикулярно главной плоскости (на рис. 4.9 эти колебания обозначены точками), а вектор Е необыкновенного луча колеблется в главной плоскости (на рис. 4.9 эти колебания показаны стрелками). Главной плоскостью или главным сечением одноосного кристалла называется плоскость, проходящая через падающий луч и пересекающую его оптическую ось (рис. 4.9 б).
Двойное лучепреломление объясняется тем, что в кристаллах диэлектрическая проницаемость ε оказывается зависящей от направления. Для одноосных кристаллов диэлектрическая проницаемость в направлении оптической оси и диэлектрическая проницаемость в направлении, перпендикулярном к ней, имеют различные значения. Поскольку абсолютный показатель преломления 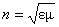 , а для большинства кристаллов магнитная проницаемость µ ≈ 1, то
, а для большинства кристаллов магнитная проницаемость µ ≈ 1, то  . Следовательно, из анизотропии диэлектрической проницаемости εвытекает анизотропия показателя преломления n.
. Следовательно, из анизотропии диэлектрической проницаемости εвытекает анизотропия показателя преломления n.
Допустим, что в точке S (рис. 4.10) внутри одноосного кристалла находится точечный источник света. На рис. 4.10 показано распространение обыкновенного и необыкновенного лучей в кристалле. Главная плоскость совпадает с плоскостью чертежа, прямая ОО' – оптическая ось. Волновая поверхность обыкновенного луча является сферой (т.к. nо = const и υо = c/nо = =const), необыкновенного луча – эллипсоид вращения (т.к.
nе ≠ const и υе = c/nо ≠ const). На рис. 4.10 хорошо видно, что наибольшее расхождение волновых поверхностных обыкновенного и необыкновенного лучей наблюдается в направлении, перпендикулярном оптической оси. Сфера и эллипсоид касаются друг друга в точках их пересечениях с оптической осью ОО'. Если υе< υо (nе>nо), то эллипсоид вписан в сферу (рис. 4.10 а), такой одноосный кристалл называется оптически положительным (например, кварц). Если υе> υо (nе<nо), то эллипсоид описан вокруг сферы (рис. 4.10 б), такой одноосный кристалл называется оптически отрицательным (например, исландский шпат, турмалин, апатит).
Некоторые кристаллы способны по-разному поглощать о- и е-лучи. Зависимость показателя поглощения среды от ориентации электрического вектора световой волны и от направления распространения света в кристалле называется дихроизмом, а сами кристаллы – дихроичными. Примером дихроичного кристалла является турмалин. При толщине
в 1 мм пластинка турмалина полностью поглощает о-лучи и свет, прошедший сквозь нее, оказывается полностью поляризованным. Дихроичные пластинки могут применяться как поляризаторы света. Еще более ярко выращенным дихроичным свойством обладают кристаллы герапатита (сернокислого йод-хинина).
4. 4. Поляризация света. @
Устройства, которые служат для поляризации света, называются поляризаторами. В качестве поляризаторов можно использовать:
- cтопу Столетова, действие которой основано на поляризации света при отражении и преломлении на границе раздела двух диэлектриков (рис. 4. 7);
- поляризационные призмы, действие которой основано на поляризации света при двойном лучепреломлении.
- поляроиды, действие которых основано на свойствах дихроичных кристаллов.
 Высококачественным поляризатором является поляризационная призма Николя (или просто николь), действие которой основано на поляризации света при двойном лучепреломлении в исландском шпате. Призма Николя (рис. 4.11) представляет собой две призмы из исландского шпата, склеенные вдоль линии АВканадским бальзамом, показатель преломления которого равен nк.б.= 1,55. Оптическая ось ОО' призмы составляет с входной гранью угол 480. Падая на грань призмыАС,естественный луч раздваивается на два луча: обыкновенный (nо= 1,66) и необыкновенный (nе= 1,51). Попадая на границу раздела "исландский шпат – канадский бальзам" обыкновенный луч испытывает полное внутреннее отражение, так как этот луч распространяется из оптически более плотной в оптически менее плотную среду (nо > nк.б. > nе) и угол падения 76,50 больше предельного угла, а затем поглощается зачерненной гранью СВ. Необыкновенный луч свободно проходит через призму и выходит из нее плоскополяризованным.
Высококачественным поляризатором является поляризационная призма Николя (или просто николь), действие которой основано на поляризации света при двойном лучепреломлении в исландском шпате. Призма Николя (рис. 4.11) представляет собой две призмы из исландского шпата, склеенные вдоль линии АВканадским бальзамом, показатель преломления которого равен nк.б.= 1,55. Оптическая ось ОО' призмы составляет с входной гранью угол 480. Падая на грань призмыАС,естественный луч раздваивается на два луча: обыкновенный (nо= 1,66) и необыкновенный (nе= 1,51). Попадая на границу раздела "исландский шпат – канадский бальзам" обыкновенный луч испытывает полное внутреннее отражение, так как этот луч распространяется из оптически более плотной в оптически менее плотную среду (nо > nк.б. > nе) и угол падения 76,50 больше предельного угла, а затем поглощается зачерненной гранью СВ. Необыкновенный луч свободно проходит через призму и выходит из нее плоскополяризованным.
Поляроиды, действие которых основано на свойствах дихроичных кристаллов, представляют собой целлулоидную пленку в которую вкраплены большое количество одинаково ориентированных кристалликов (например, геропатита). Поляроиды по сравнению с призмами менее прозрачны и в них степень поляризации сильно зависит от длины волны падающего света. Преимуществом перед призмами является только то, что их можно изготовить с большей площадью поверхности.
4. 5. Анализ плоскополяризованного света. Закон Малюса. @
Глаз человека не может отличить поляризованный свет от естественного, поэтому для анализа поляризованного свет необходимо использовать поляризаторы, которые в этом случае называются анализаторами. Все ранее перечисленные поляризующие устройства можно использовать для анализа поляризации света. Анализировать поляризованность света первым предложил французский физик Э. Малюс (1775-1812), установив закон изменения интенсивности поляризованного света.
Возьмем в качестве поляризатора и анализатора дихроичный кристалл турмалин (рис. 4.12). Пусть естественный свет падает перпендикулярно оптической оси ОО' поляризатора П. Через поляризатор свободно пройдут колебания светового вектора, параллельные плоскости поляризатора. Колебания светового вектора, перпендикулярные плоскости поляризации, полностью поглотятся кристаллом турмалина. Ранее уже говорилось о том, что любое колебание вектора Ес можно представить как результат сложения двух взаимно перпендикулярных векторов Ех и Еу (рис. 4. 2), а так как колебания вектора Ес естественного света хаотичны и равновероятны, то интенсивность света, прошедшего через поляризатор, равна половине интенсивности падающего естественного света:

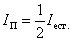
Если плоско поляризованный свет падает на анализатор А (рис. 4.13), то через него пройдет только составляющая, параллельная главной плоскости анализатора:
Е = Е0 cosj,
где j - угол между плоскостями поляризации поляризатора и анализатора. Так как интенсивность света пропорциональна квадрату амплитуды (I ~ E2) ,то для интенсивности света I, вышедшего из анализатора получаем:
 I = I0 cos2j,
I = I0 cos2j,
где I0 – интенсивность света, падающего на анализатор. Этот закон называется законом Малюса. Если естественный свет с интенсивностью Iест проходит последовательно сквозь поляризатор и анализатор, то выходящий свет имеет интенсивность
 .
.
При j = 0 (плоскости поляризатора и анализатора параллельны) интенсивность максимальна Imax = 1/2 Iест, при j = π/2 (плоскости поляризатора и анализатора взаимно перпендикулярны) интенсивность минимальна Imin = 0.
Для анализа поляризованности света анализатор нужно вращать вокруг луча, если при этом можно найти такое положение, при котором свет сквозь него не проходит (интенсивность становится равной нулю), то такой свет полностью поляризован; если при вращении анализатора интенсивность света не изменяется, такой свет будет естественный.
4. 6. Интерференция поляризованных лучей. @
Цуги волн естественного света некогерентны, так как соответствуют излучению различных, независимых атомов источника света. При прохождении естественного света через одноосный анизотропный кристаллразные цуги участвуют в образовании обыкновенного и необыкновенного лучей. Поэтому они некогерентны. Если же пропустить через одноосный анизотропный кристалл плоско поляризованный свет, то обыкновенный и необыкновенный свет будут когерентны и при определенных условиях могут интерферировать. На рис. 4.15 представлена оптическая схема, позволяющая наблюдать интерференцию поляризованного света. Естественный свет, пройдя через поляризатор становится плоско поляризованным. Далее он попадает на пластинку, вырезанную из одноосного анизотропного кристалла параллельно оптической оси. Внутри пластинки он разбивается на два луча обыкновенный "о" и необыкновенный "е", которые пространственно не разделены, но движутся с разными скоростями. За время прохождения через пластинку между ними возникает разность хода
Δ = (no-ne) d
где d – толщина пластины. Хотя эти лучи когерентны и имеют оптическую разность хода, но они не могут  интерферировать, так как вектора колебания Ео и Ее лежат во взаимно перпендикулярных плоскостях. Поэтому, чтобы получить интерференционную картинку необходимо совместить плоскости колебаний этих волн. Для этого применяют анализатор.
интерферировать, так как вектора колебания Ео и Ее лежат во взаимно перпендикулярных плоскостях. Поэтому, чтобы получить интерференционную картинку необходимо совместить плоскости колебаний этих волн. Для этого применяют анализатор.
Анализатор (рис. 4.16) пропустит только ту составляющую каждого из векторов (на рисунке это вектора Ее' и Ео' ), которая будет параллельна плоскости анализатора (ОО'). Интерференционная картина, наблюдаемая на выходе из анализатора, зависит от многих факторов, таких как разности фаз, длины волны падающего света, от угла между осью поляризатора и оптической осью двояко преломляющей пластины и т. д.
4. 7. Искусственная оптическая анизотропия. @
Оптически изотропные вещества могут стать анизотропными под действием ряда внешних воздействий, это явление называют искусственной оптической анизотропией.
Фотоупругость (или пьезооптический эффект) - возникновение оптической анизотропии в первоначально изотропных веществах под воздействием механических напряжений Этот эффект первыми обнаружили Т. Зеебек (1813г.) и Д. Брюстер (1816г.). Например, при одностороннем сжатии или растяжении стеклянная пластина приобретает свойства одноосного кристалла, оптическая ось которого совпадает с направлением сжатия или растяжения. При этом разность показателей преломления обыкновенного и необыкновенного лучей в направлении, перпендикулярном оптической оси, пропорциональна напряжению σ
no – ne = k σ,
где k – коэффициент, зависящий от свойств вещества. Явление искусственной оптической анизотропии при деформациях используется для обнаружения остаточных внутренних напряжений, которые могут возникать в изделиях из стекла и других прозрачных изотропных материалов вследствие несоблюдения технологии их изготовления. Оптический метод изучения на прозрачных моделях распределения внутренних напряжений, возникающих в различных деталях машин и сооружений широко применяется в современной технике.
Эффект Керра – Д. Керр (1875г.) исследовал связь между оптическими и электрическими явлениями и установил, что оптически изотропный диэлектрик в достаточно сильном электрическом поле приобретает свойства одноосного двояко преломляющего кристалла, оптическая ось которого совпадает с направлением напряженности электрического поля.
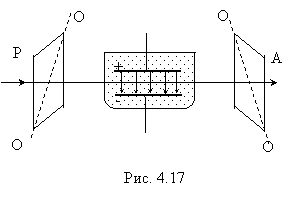 Схема установки для исследования эффекта Керра показана на рис. Ячейку Керра поместили между скрещенными поляризатором и анализатором. Ячейка Керра представляет собой герметичный сосуд а с жидкостью, в которую погружены обкладки плоского конденсатора. При подаче на пластины напряжения между ними возникает однородное электрическое поле. Под действием этого поля жидкость приобретает свойства одноосного кристалла, оптическая ось которого ориентирована вдоль поля. Возникающая разность показателей преломления no и ne пропорциональна квадрату напряженности поля Е
Схема установки для исследования эффекта Керра показана на рис. Ячейку Керра поместили между скрещенными поляризатором и анализатором. Ячейка Керра представляет собой герметичный сосуд а с жидкостью, в которую погружены обкладки плоского конденсатора. При подаче на пластины напряжения между ними возникает однородное электрическое поле. Под действием этого поля жидкость приобретает свойства одноосного кристалла, оптическая ось которого ориентирована вдоль поля. Возникающая разность показателей преломления no и ne пропорциональна квадрату напряженности поля Е
no – ne = k Е2,
или разность фаз
 или
или 
где В – постоянная Керра, зависящая от природы вещества, длины волны λ0 и температуры, l – длина ячейки Керра.
Эффект Керра объясняется различной поляризуемостью молекул по разным направлениям. В отсутствие поля молекулы ориентированы хаотично, поэтому жидкость не обладает анизотропией, Под действием поля молекулы поворачиваются так, чтобы в направлении поля были ориентированы либо их дипольные электрические моменты (у полярных молекул), либо направление наибольшей поляризуемости (у неполярных молекул). В результате жидкость становится оптически активной. Эффект Керра безынерционен: время, за которое вещество переходит из анизотропное состояние в изотропное и обратно, не превышает 10-9с. Ячейки Керра применяются при записи звука на кинопленку, а в сочетании со скещенными поляризатором и анализатором в скоростной съемке.
Эффект Коттона–Мутона (аналог эффекта Керра в магнитном поле)- это явление возникновения оптической анизотропии у некоторых веществ при помещении их в магнитное поле. В достаточно сильных магнитных полях возникает анизотропия, появляется двойное лучепреломление. В этом случае среда ведет себя как оптически одноосный кристалл, ось которого совпадает по направлению с вектором напряженности магнитного поля H. Возникающая разность показателей преломления для необыкновенного и обыкновенного лучей монохроматического света при его распространении в направлении, перпендикулярном вектору Н, и пропорциональна квадрату напряженности поля Н:
nе – no = Cλ0 H2
где C – постоянная Коттона–Мутона, зависящая от природы вещества, длины волны λ0 и температуры.
Линейный электрооптический эффект Поккельса – явление изменения двойного лучепреломления вещества из-за смещения собственной частоты во внешнем электрическом поле:
nе – no = αE.
В отличие от эффекта Керраэлектрооптический эффект Поккельса пропорционален напряженности электрического поля.
4. 8. Оптическая активность веществ. @
При пропускании плоско поляризованного света через некоторые вещества наблюдается вращение плоскости поляризации. Вещества, способные вращать плоскость поляризации, называются оптически активными. Оптической активностью могут обладать кристаллы (кварц, киноварь), жидкости (скипидар, винная кислота), растворы оптически активных веществ в неактивных растворителях (водные растворы сахара, яблочной кислоты, спиртовые растворы камфоры, стрихнина). Оптическую активность проявляют многие природные соединения: белки, углеводы, гормоны, эфирные масла.
Угол поворота j плоскости поляризации для оптически активных кристаллов и чистых жидкостей
j = α d
где α –постоянная вращения, угол поворота плоскости поляризации слоем вещества единичной толщины; d – расстояние, пройденное светом в оптически активном веществе. Постоянная вращения зависит от природы вещества, температуры и длины волны света. Зависимость α от λ, называется дисперсией вращения. Наибольшей оптической активностью обладают некоторые жидкие кристаллы.
Угол поворота j плоскости поляризации для оптически активных растворов (закон Био)
j = [α] с d
где [α] – удельное вращение, с – массовая концентрация оптически активного вещества, d – расстояние, пройденное светом в оптически активном веществе.
Оптическая активность обуславливается как асимметричным строением молекул вещества, так и расположением частиц в кристаллической решетке. В зависимости от направления вращения плоскости поляризации оптические вещества делятся на право- и левовращающие. В первом случая осуществляется вращение плоскости вправо (по часовой стрелке), во втором – влево (против часовой стрелке).


|








|

|
|
|
|
|
|


|
|




|
|
|
|
|
|




|

|

Вращение плоскости поляризации объяснено О. Френелем (1823г.). Он предложил (рис. 4.18 а) линейно поляризованную монохроматическую волну представить в виде комбинации двух одновременно распространяющихся поляризованных по кругу монохроматических волн, векторы напряженностей Е1 и Е2 у которых равны половине амплитуды вектора Е и вращаются во взаимно противоположных направлениях с одинаковыми угловыми скоростями (рис. 4.18 б). В оптически активной среде волны Е1 и Е2 распространяются с разными фазовыми скоростями. На выходе из слоя толщиной l волны Е1 и Е2 складываются (рис.4.18 в), но между ними возникает сдвиг фаз Δj, пропорциональный толщине слоя l. Плоскость поляризации на выходе (О'О') оказывается повернутой относительно плоскости поляризации на входе (ОО) на угол поворота Δj/2.
М. Фарадеем (1845г.) было установлено, что вещества, не обладающие естественной оптической активностью, приобретают ее под действием магнитного поля. Это явление называется эффектом Фарадея или магнитное вращение плоскости поляризации. Угол поворота плоскости поляризации пропорционален напряженности магнитного поля Н, длине пути света в веществе l.
j = V H l
где V – постоянная Верде (или удельным магнитным вращением), которая зависит от природу вещества и длины волны света. Направление магнитного вращения плоскости поляризации определяется направлением магнитного поля и не зависит от направления распространения луча. Так, если отразить луч света с помощью зеркала и заставить пройти через намагниченное вещество еще раз только в обратном направлении, то угол поворота плоскости поляризации удвоится. Этим эффект Фарадея отличается от вращения плоскости поляризации света в естественных оптически активных средах.
Магнитное вращение плоскости поляризации обусловлено возникающей под действием магнитного поля прецессией электронных орбит. Оптически активное вещество под действием магнитного поля приобретает дополнительную способность вращать плоскость поляризации и угол поворота будет равен сумме углов поворота при естественной и искусственной оптических активностей.
Явления вращения плоскости поляризации лежат в основе метода определения концентрации растворов оптически активных веществ. Этот метод называется поляриметрией, а при определении содержания сахара сахариметрией. Они успешно используются в пищевой промышленности, в медицине, при исследовании биополимеров.
5. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОМЕГНИТНЫХ ВОЛН С ВЕЩЕСТВОМ. @
Переменное электромагнитное поле световой волны, распространяющейся в диэлектрической среде, вызывает вынужденные колебания связанных зарядов (электронов и ионов), входящих в состав молекул среды, т.е. свет взаимодействует с веществом. Внешние электроны диэлектрика связаны с атомом не жестко и под влиянием внешнего поля электромагнитной волны испытывают смещение. Это смещение описывается гармонической функцией, т.е. электрон совершает гармонические колебания. Результатом таких колебаний являются вторичные волны, источниками которых являются электроны вещества. Рассмотрим несколько частных случаев взаимодействия световых волн с веществом.
5. 1. Поглощение света. @
Пусть на вещество (это может быть газ, жидкость или твердое тело) падает электромагнитная волна. Из оптических опытов известно, что по мере распространения световой волны в веществе ее интенсивность постепенно уменьшается. Явление уменьшения энергии световой волны при ее распространении в веществе, происходящее вследствие преобразования энергии волны во внутреннюю энергию веществав или энергию вторичного излучения, имеющего другой спектр и другие направления распространения, называется поглощением света. Поглощение света может вызвать нагревание вещества, возбуждение или ионизацию атомов, а также другие процессы в веществе.
В 1729 г. один из основателей фотометрии французский ученый Пьер Бугер эспериментально установил закон поглощения света, который позднее, в 1760 г. теоретически был доказан немецким ученым Иоганном Генрихом Ламбертом. Закон, получивший названиезакона Бугера – Ламберта, имеет вид:
 ,
,
где I0 и I – интенсивности световой волны на входе и выходе из вещества, α – показатель поглощения среды, который зависит от химической природы и состояния вещества, а также от длины волны падающего света и не зависит от его интенсивности. α показывает обратную толщину, по мере прохождения которой I0 уменьшается в е =2,72 раз. Для разбавленных растворов показатель поглощения пропорционален концентрации раствора с (закон Бера): α=сb, где b – постоянная Бера, не зависящая от концентрации. Интенсивность световой волны, прошедшей через разбавленный раствор определяется законом Бугера-Ламберта-Бера:  .
.
Вещества, в которых атомы находятся на значительных расстояниях друг от друга (газы, пары металлов) обладают так назывемыми линейчатыми спектрами поглощения. Это значит, что их α близок к нулю и только в очень узких спектральных областях порядка 10-12-10-11м α достигает больших значений (рис.). Происходит это в области частот, близких к собсвенным частотам колебания электронов в атомах. Диэлектрики поглощают свет более-менее селективно и для них наблюдаются широкие области, где α отличен от нуля, т.е. жидкие и твердые диэлектрики имеют сплошной спектр поглощения. Металлы непрозрачны для света. Они содержат огромное число электронов проводимости, которые под действием света совершают переменное движение и излучают вторичные волны. В результате наложения первичной волны, падающей на поверхность металла, и вторичных волн образуется интенсивная отраженная волна и сравнительно слабая волна, проходящая в металле.
5. 2. Дисперсия света. @
Электромагнитная волна, а, значит, и световая волна, распространяется внутри вещества с фазовой скоростью υ < c. Напомним, что фазовая скорость υ = ω ⁄ k – это скорость распространения определенной фазы волны. Отношение n =с / υ, то есть абсолютный показатель преломления среды показывает, во сколько раз скорость света в вакууме больше скорости света в данной среде (см. раздел 1.1).
Зависимость показателя преломления n вещества от частоты или длины волны падающего на вещество света называется дисперсией света:
n = f(ν); n = f(λ).
Фазовая скорость света, следовательно, также есть функция частоты или длины волны света:
υ = f(ν); υ = f(λ).
 Следствием дисперсии световых волн является разложение пучка белого света в спектр при прохождении его через призму. Призматические спектры были известны людям издавна, стеклянные призмы даже продавались для развлечения. Это явление объяснил Ньютон 6 февраля 1672 г. на заседании Королевского научного общества, сделав сообщение на тему “Новая теория света и цветов”. В этом сообщении Ньютон утверждал, что “наиболее удивительная и чудесная смесь цветов – белый свет”. Явление разложения белого света на составляющие Ньютон назвал дисперсией (от лат. dispersio - рассеяние). Призматический спектр изображен на рис. В данном случае, в отличие от дифракционных спектров, свет более коротких волн (фиолетовых) преломляется призмой больше, чем длинных (красных).
Следствием дисперсии световых волн является разложение пучка белого света в спектр при прохождении его через призму. Призматические спектры были известны людям издавна, стеклянные призмы даже продавались для развлечения. Это явление объяснил Ньютон 6 февраля 1672 г. на заседании Королевского научного общества, сделав сообщение на тему “Новая теория света и цветов”. В этом сообщении Ньютон утверждал, что “наиболее удивительная и чудесная смесь цветов – белый свет”. Явление разложения белого света на составляющие Ньютон назвал дисперсией (от лат. dispersio - рассеяние). Призматический спектр изображен на рис. В данном случае, в отличие от дифракционных спектров, свет более коротких волн (фиолетовых) преломляется призмой больше, чем длинных (красных).
Призма располагает световые лучи в спектр по значениям показателя преломления n, который для всех прозрачных веществ с увеличением длины волны уменьшается.
Зависимость n(ν) или n(λ) имеет нелинейный и немонотонный характер. Существуют области частот, для которых n увеличивается с ростом ν (или, что то же самое, уменьшается с ростом λ). Для этих областей частот выполняются условия:
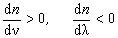 .
.
 В данном случае мы имеем дело с нормальной дисперсией света. Нормальная дисперсия наблюдается у веществ, прозрачных для света. Например, обычное стекло прозрачно для видимого света и в данном диапазоне частот наблюдается нормальная дисперсия света в стекле. При нормальной дисперсии групповая скорость световых волн в веществе u < υ.
В данном случае мы имеем дело с нормальной дисперсией света. Нормальная дисперсия наблюдается у веществ, прозрачных для света. Например, обычное стекло прозрачно для видимого света и в данном диапазоне частот наблюдается нормальная дисперсия света в стекле. При нормальной дисперсии групповая скорость световых волн в веществе u < υ.
Дисперсия света называется аномальной, если с ростом частоты показатель преломления уменьшается (или с ростом длины волны - увеличивается), т.е.
 .
.
У обычного стекла аномальная дисперсия обнаруживается в ультрафиолетовом и инфракрасном диапазоне световых волн. При аномальной дисперсии групповая скорость больше фазовой u > υ.
Явление дисперсии объясняется с помощью электронной теории Лоренца. В этой теории дисперсия света рассматривается как результат взаимодействия электромагнитных волн с заряженными частицами, входящими в состав вещества и совершающими вынужденные колебания в переменном электромагнитном поле волны с частотой данной волны. При приближении частоты световой волны к частоте собственных колебаний электронов возникает явление резонанса, обусловливающее поглощение света. Наличие собственной частоты колебаний приводит к зависимости n от ν, передающей весь ход дисперсии света как вблизи полос поглощения, так и вдали от них (рис. 5.2). На рис. 5.2 АВ – область аномальной дисперсии, наблюдающейся вблизи резонансной частоты, остальные участки описывают аномальную дисперсию.
Отношение  называется дисперсией вещества.
называется дисперсией вещества.
Дисперсией света объясняется явление радуги, игра цветов в драгоценных камнях и на хрустале и многие другие явления.
5. 3. Отражение и пропускание света. Окраска тел в природе. @
Отражение света – это явление, заключающееся в том, что при падении света из первой среды на границу раздела со второй средой взаимодействие света с веществом приводит к появлению световой волны, распространяющейся от границы раздела в первую среду.Несамосветящиеся тела становятся видимыми благодаря отражению света от их поверхности. Данное явление тесно связано с явлениями преломления и поглощения света.
Интенсивность отраженного света зависит от угла падения, поляризации падающего пучка лучей, показателей преломления обеих сред и характеризуется коэффициентом отражения R:  , где Iотр – интенсивность отраженного света. Коэффициент отражения всегда меньше единицы. Если неровности поверхности границы раздела малы по сравнению с длиной волны падающего света, то имеет место правильное, или зеркальное отражение света. Если же размеры неровностей соизмеримы с длиной волны или больше нее, то отражение называется диффузным. При зеркальном отражении фаза отраженного луча скачкообразно меняется. В случае нормального падения на оптически более плотную среду фаза отраженной волны сдвигается на π. Наибольшим коэффициентом отражения обладают металлы и именно этим объясняется использование металлизированных поверхностей в зеркалах.
, где Iотр – интенсивность отраженного света. Коэффициент отражения всегда меньше единицы. Если неровности поверхности границы раздела малы по сравнению с длиной волны падающего света, то имеет место правильное, или зеркальное отражение света. Если же размеры неровностей соизмеримы с длиной волны или больше нее, то отражение называется диффузным. При зеркальном отражении фаза отраженного луча скачкообразно меняется. В случае нормального падения на оптически более плотную среду фаза отраженной волны сдвигается на π. Наибольшим коэффициентом отражения обладают металлы и именно этим объясняется использование металлизированных поверхностей в зеркалах.
Пропускание света – это прохождение сквозь среду оптического излучения без изменения набора частот составляющих его монохроматических излучений и их относительной интенсивности. Процесс пропускания характеризуется коэффициентом пропускания Т, который зависит от размеров тела и состояния его поверхности, а также от спектрального состава, угла падения и поляризации излучения:
 , где Iпроп – интенсивность света, пропущенного веществом. Коэффициент пропускания также всегда меньше единицы. Лучше всего пропускают свет прозрачные тела. Так, коэффициент пропускания обычного стекла близок к единице.
, где Iпроп – интенсивность света, пропущенного веществом. Коэффициент пропускания также всегда меньше единицы. Лучше всего пропускают свет прозрачные тела. Так, коэффициент пропускания обычного стекла близок к единице.
На основе вышеизложенного материала можно понять, от чего зависит окраска окружающих нас тел. Каждое тело, взаимодействуя со светом, имеет способность поглощать, пропускать или отражать свет тех или иных длин волн. Если тело хорошо поглощает падающий на него свет, а отражает и пропускает плохо, оно черное и непрозрачное, как, например, сажа. Белые тела наоборот хорошо отражают падающий на них свет, а поглощают плохо. Окраска всех непрозрачных тел определяется тем, какие длины волн тело лучше отражает. Тело, для которого коэффициент отражения красных длин волн значительно больше коэффициентов отражения других волн, будет красным и т.п. Окраска всех прозрачных тел определяется тем, какие длины волн тело лучше пропускает. Прозрачное тело будет бесцветным, если оно поглощает свет всех цветов в одинаковой мере и таким образом, в прошедшем свете не будет нарушено соотношение между различными составляющими белого света. Если же прозрачное тело обладает избирательным поглощением, то оно приобретает определенную окраску. Прозрачное тело, для которого коэффициент пропускания фиолетовых длин волн значительно больше коэффициентов пропускания других волн, будет фиолетовым и т.п. На этом свойстве основано изготовление светофильтров. Например, красный светофильтр изготавливают из стекла, которое менее всех поглощает и лучше всех пропускает свет красных длин волн. Если на такое стекло направить зеленый или синий свет, то оно будет казаться черным.
6. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ ТЕЛ. @
Электромагнитное излучение, испускаемое атомами тела за счет внутренней (тепловой) энергии излучающего тела и зависящее только от температуры и оптических свойств данного тела, называется тепловым. Этот вид излучения происходит при всех температурах и представляет для физиков особый интерес, так как это единственное излучение, которое может находиться в состоянии термодинамического равновесия с нагретыми телами.
Нагретые тела обмениваются энергией только путем испускания и поглощения лучистой энергии. В состоянии равновесия процессы испускания и поглощения энергии каждым телом в среднем компенсируют друг друга, и в пространстве между телами характеристики излучения достигают определенных значений, зависящих только от установившейся температуры тел. Это излучение, находящееся в термодинамическом равновесии с телами, имеющими одинаковую температуру, называется равновесным или черным излучением. Величина энергии равновесного излучения и его спектральный состав зависят только от температуры. Если в адиабатно замкнутую полость с зеркально отражающими стенками поместить несколько тел, нагретых до различной температуры, то, как показывает опыт, такая система с течением времени приходит в состояние теплового равновесия, при котором все тела приобретают одинаковую температуру. Если через малое отверстие заглянуть внутрь полости, в которой установилось термодинамическое равновесие между излучением и нагретыми телами, то глаз не различит очертаний тел и зафиксирует лишь однородное свечение всей полости в целом.
Для установления равновесия в полости необходимо, чтобы каждое тело испускало ровно столько лучистой энергии, сколько оно и поглощает. Это одна из важнейших закономерностей теплового излучения, экспериментально установленная Прево в 1809 г.
6. 1. Характеристики теплового излучения. @
Рассмотрим величины, характеризующие тепловое излучение:
1. Энергетическая светимость R(Т) - это полная энергия электромагнитного излучения, испускаемая единицей поверхности тела во всех направлениях в единицу времени на всех частотах. Этот полный поток излучения всех волнназывают также интегральной светимостью тела. Согласно определению

2. Распределение энергии по длинам волн в излучении тел при заданной температуре T характеризуется испускательной или излучательной способностью  илиr(ν, T), равной энергии, испускаемой с единицы поверхности тела в единицу времени в единичном интервале частот. Аналогично можно ввести распределение энергии по длинам волн r(λ, T). Функцию r(λ, T) (или r(ν, T)) часто называют спектральной плотностью энергетической светимости.
илиr(ν, T), равной энергии, испускаемой с единицы поверхности тела в единицу времени в единичном интервале частот. Аналогично можно ввести распределение энергии по длинам волн r(λ, T). Функцию r(λ, T) (или r(ν, T)) часто называют спектральной плотностью энергетической светимости.

Связь энергетической светимости и испускательной способности тела записывается следующим образом:

3. Способность тел поглощать падающее на них излучение характеризуется поглощательной способностью  или а(ν,Т)- отношением поглощенной энергии в интервале частот от ν до ν +dν к общему количеству энергии падающего излучения в том же интервале:
или а(ν,Т)- отношением поглощенной энергии в интервале частот от ν до ν +dν к общему количеству энергии падающего излучения в том же интервале:

Поглощательная способность - это безразмерная величина.
 Испускательная и поглощательная способности зависят от частоты излучаемых и поглощаемых волн, температуры тела, его химического состава и состояния поверхности. Все тела частично поглощают и частично отражают падающее на них излучение. Идеализацией является понятие абсолютно черного тела, поглощающего все падающее на него излучение во всем диапазоне частот. Поглощательная способность абсолютно черного тела равна единице
Испускательная и поглощательная способности зависят от частоты излучаемых и поглощаемых волн, температуры тела, его химического состава и состояния поверхности. Все тела частично поглощают и частично отражают падающее на них излучение. Идеализацией является понятие абсолютно черного тела, поглощающего все падающее на него излучение во всем диапазоне частот. Поглощательная способность абсолютно черного тела равна единице  = 1 при любой температуре T . Моделью абсолютно черного тела является небольшое отверстие в сферической полости, размер отверстия меньше 0.1 от диаметра полости (рис. 6.1). Свет, падающий через отверстие внутрь полости, после поглощения и отражения стенками будет такой системой практически полностью поглощен, и отверстие снаружи будет казаться совершенно черным. Но если полость нагрета до определенной температуры T, и внутри установилось тепловое равновесие, то собственное излучение полости, выходящее через отверстие, будет излучением абсолютно черного тела. Именно таким образом моделируется абсолютно черное тело во всех экспериментах по исследованию теплового излучения. Абсолютно черных тел в природе не бывает. В природе к абсолютно черному телу по свойствам близки: сажа, черный бархат, черная шерсть животных, поглощающие свойства которых обусловлены их пористостью. От таких тел падающее излучение не отражается из-за многократного переотражения в микрополостях и последующего рассеяния.
= 1 при любой температуре T . Моделью абсолютно черного тела является небольшое отверстие в сферической полости, размер отверстия меньше 0.1 от диаметра полости (рис. 6.1). Свет, падающий через отверстие внутрь полости, после поглощения и отражения стенками будет такой системой практически полностью поглощен, и отверстие снаружи будет казаться совершенно черным. Но если полость нагрета до определенной температуры T, и внутри установилось тепловое равновесие, то собственное излучение полости, выходящее через отверстие, будет излучением абсолютно черного тела. Именно таким образом моделируется абсолютно черное тело во всех экспериментах по исследованию теплового излучения. Абсолютно черных тел в природе не бывает. В природе к абсолютно черному телу по свойствам близки: сажа, черный бархат, черная шерсть животных, поглощающие свойства которых обусловлены их пористостью. От таких тел падающее излучение не отражается из-за многократного переотражения в микрополостях и последующего рассеяния.
Наряду с понятием черного тела используют понятие серого тела, поглощательная способность которого меньше единицы, но одинакова для всех частот и зависит только от температуры, материала, из которого сделано тело и состояния его поверхности
 .
.
У реальных тел  < 1 и зависит от частоты.
< 1 и зависит от частоты.
6. 2. Закон Кирхгофа. @
Кирхгоф (1859 г.) нашел количественную связь излучательной и поглощательной способности: отношение излучательной и поглощательной способности не зависит от природы тела и является универсальной функцией частоты и температуры, одинаковой для всех тел:
 ,
,
где функция f(ν,T) называется универсальной функцией Кирхгофа. Этот закон следует из того, что для теплового равновесия количества поглощаемой и излучаемой телом энергии должны быть равны для всех диапазонов частот:
 .
.
Это равенство можно переписать в следующем виде:  , откуда следует
, откуда следует

где f(ν,T)- общая для всех тел функция, характеризующая распределение энергии по частотам в падающем на тела тепловом излучении. Закон справедлив для любого тела, в том числе и для абсолютно черного. Поскольку его поглощательная способность равна единице, то из закона следует 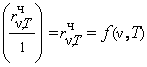 . Таким образом, универсальная функция Кирхгофа есть не что иное, как испускательная способность абсолютно черного тела. Из закона Кирхгофа следует, что испускательная способность любого тела меньше, чем абсолютно черного.
. Таким образом, универсальная функция Кирхгофа есть не что иное, как испускательная способность абсолютно черного тела. Из закона Кирхгофа следует, что испускательная способность любого тела меньше, чем абсолютно черного.
6. 3. Законы Стефана-Больцмана и Вина. @
Открытие закона Кирхгофа потребовало тщательного изучения излучения абсолютно черного тела. В 1879 году польский физик Йозеф Стефан на основе анализа экспериментальных данных пришел к заключению, что энергетическая светимость абсолютно черного тела R(T) пропорциональна четвертой степени абсолютной температуры T:
R(T) = sT4
Несколько позднее, в 1884 году, Л. Больцман теоретически получил эту зависимость на основе термодинамических законов. Этот закон получил название закона Стефана–Больцмана. Числовое значение постоянной Стефана-Больцмана σ составляет 5,671·10–8 Вт/(м2·К4). В дальнейшем в результате экпериментальных проверок было установлено, что такая зависимость с поправкой имеет место и для других тел.
 Закон Стефана-Больцмана не позволяет найти частотную зависимость излучения.Лишь к концу 90-х годов XIX века были выполнены тщательные экспериментальные измерения спектрального распределения излучения абсолютно черного тела, которые показали, что при каждом значении температуры T зависимость r(λ, T) имеет свой ярко выраженный максимум (рис. 6.2). С увеличением температуры максимум смещается в область коротких длин волн, причем произведение температуры T на длину волны λm, соответствующую максимуму, остается постоянным:
Закон Стефана-Больцмана не позволяет найти частотную зависимость излучения.Лишь к концу 90-х годов XIX века были выполнены тщательные экспериментальные измерения спектрального распределения излучения абсолютно черного тела, которые показали, что при каждом значении температуры T зависимость r(λ, T) имеет свой ярко выраженный максимум (рис. 6.2). С увеличением температуры максимум смещается в область коротких длин волн, причем произведение температуры T на длину волны λm, соответствующую максимуму, остается постоянным:
λmT = b или λm = b / T.
Это соотношение было получено Вином в 1893 г. из термодинамики. Оно выражает так называемый закон смещения Вина: длина волны λm, на которую приходится максимум энергии излучения абсолютно черного тела, обратно пропорциональна абсолютной температуре T. Значение постоянной Вина b = 2,898·10–3 м·К.
При практически достижимых в лабораторных условиях температурах максимум излучательной способности r(λ, T) лежит в видимой красной и инфракрасной областях, поэтому нагретые тела приобретают красный цвет. Вид графиков (рис. 6.2) показывает, как спектральный максимум излучения смещается из инфракрасной в видимую (при T ≥ 5·103 К) и далее в ультрафиолетовую область при повышении температуры тела, что подтверждается экспериментально. Максимум энергии излучения Солнца приходится примерно на 470 нм (зелено-голубая область спектра), что соответствует температуре наружных слоев Солнца около 6200 К (если рассматривать Солнце как абсолютно черное тело).
6. 4. Квантовый характер излучения. @
После установления законов излучения стало очевидно, что первоочередная задача теории теплового излучения состоит в нахождении вида функции Кирхгофа, т.е. выяснение спектрального состава равновесного излучения абсолютно черного тела. Решение этой задачи вышло далеко за рамки теории излучения и сыграло огромную роль во всем дальнейшем развитии физики, т.к. привело к установлению квантового характера излучения и поглощения энергии атомами и молекулами.
Существование на экспериментальных кривых (рис. 6.2) максимумов свидетельствует о том, что энергия излучения черного тела распределена по его спектру неравномерно – черное тело почти не излучает в области очень малых и очень больших частот.
В 1900 году эту проблему пытался решить знаменитый английский физик, барон Д.У. Релей, который в основу своих рассуждений положил теорему классической статистической механики о равномерном распределении энергии по степеням свободы в состоянии термодинамического равновесия. Эта теорема была применена Релеем к равновесному излучению в полости. Равновесное электромагнитное излучение в замкнутой полости c постоянной температурой стенок он рассматривал как систему стоячих электромагнитных волн различных частот в 3-х измерениях. Колебания с различными частотами совершаются независимо друг от друга и каждой частоте соответствует своя колебательная степень свободы. Несколько позже эту идею подробно развил английский физик и астроном Д.Х.Джинс. Таким путем удалось получить зависимость излучательной способности абсолютно черного тела от частоты n и температуры T:


Это соотношение называют формулой Релея–Джинса. Оно согласуется с экспериментальными данными только в области достаточно длинных волн или малых частот (рис. 6.3). Кроме того, из него следует абсурдный вывод о том, что интегральная светимость R(T) черного тела должна обращаться при коротких (ультрафиолетовых) длинах волн в бесконечность, что было названо «ультрафиолетовой катастрофой» и что противоречило реально наблюдаемым данным.
Таким образом, безупречный с точки зрения классической физики вывод приводит к формуле, которая находится в резком противоречии с опытом. Стало ясно, что решить задачу о спектральном распределении излучения абсолютно черного тела в рамках существующих теорий невозможно. Эта задача была успешно решена немецким физиком М. Планком на основе новой идеи, положившей начало квантовой физике.
В своих расчетах Планк выбрал наиболее простую модель изл
Дата добавления: 2015-01-05; просмотров: 969; Мы поможем в написании вашей работы!; Нарушение авторских прав |