
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Показание U1 вольтметра, подключенного к точкам А и В (рис
Показание U1 вольтметра, подключенного к точкам А и В (рис. 7.1), определяется по закону Ома:
U1=I1R1, (1)
где I1 – сила тока в неразветвлённой части цепи; R1 – сопротивление параллельно соединенных вольтметра и половины потенциометра.
Силу тока I1 найдем по закону Ома для всей цепи:

 , (2)
, (2)
где 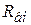 – сопротивление внешней цепи.
– сопротивление внешней цепи.
Внешнее сопротивление 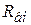 есть сумма двух сопротивлений:
есть сумма двух сопротивлений:
 . (3)
. (3)
Сопротивление R1 параллельного соединения может быть найдено по формуле 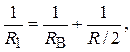 откуда
откуда
Rl=R∙RB/(R + 2RB).
Вычисления: Rl=100∙500/(100 + 2.500)=45.5 Ом.
Подставив в выражение (2) выражение для 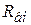 из (3), определим силу тока:
из (3), определим силу тока:
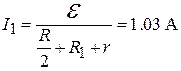 .
.
Если подставить значения I1 и R1 в формулу (1), то найдем показание вольтметра: U1=46,9 В.
Разность потенциалов между точками А и В при отключенном вольтметре равна произведению силы тока I2 на половину сопротивления потенциометра:
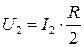 ,
,
причём 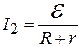 . Тогда
. Тогда 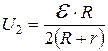 . Вычисления:
. Вычисления:  .
.
Ответ: U2=50 В.
 8. Электромагнетизм
8. Электромагнетизм
Краткая теория
· Магнитный момент контура с током:
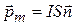 ,
,
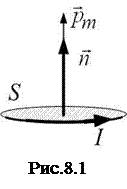
где I – сила тока в контуре, S – его площадь, 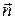 – единичный вектор нормали к контуру (рис.8.1). Если контур имеет N витков, то
– единичный вектор нормали к контуру (рис.8.1). Если контур имеет N витков, то 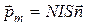 .
.
· Индукция магнитного поля В – отношение максимального вращающего момента Мmax к магнитному моменту 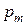 контура:
контура:
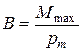
· Принцип суперпозиции: если в данной точке пространства различные источники создают магнитные поля, магнитные индукции которых равны 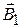 ,
, 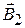 …,
…, 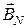 , то результирующая индукция поля в этой точке равна:
, то результирующая индукция поля в этой точке равна:
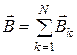 .
.
· Закон Ампера. Сила, действующая на проводник с током в магнитном поле (сила Ампера), направлена по правилу левой руки (рис.8.2) и равна
F=B∙I∙l∙sinα,
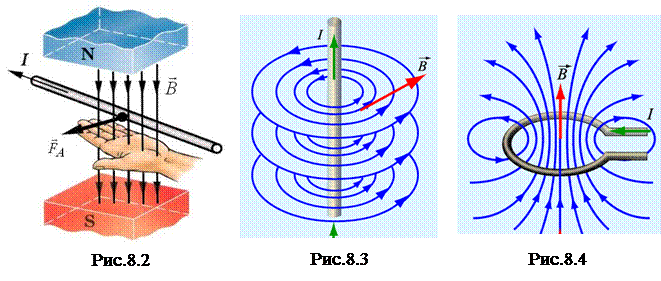 где I – сила тока; l – длина проводника;
где I – сила тока; l – длина проводника; 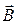 – магнитная индукция поля, α – угол между проводником и вектором
– магнитная индукция поля, α – угол между проводником и вектором 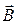 .
.
· Индукция магнитного поля прямолинейного проводника с током I бесконечной длины на расстоянии r от проводника:
 ,
,
где 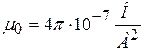 – магнитная постоянная, μ – магнитная проницаемость среды (для вакуума μ=1). Направление тока и магнитной индукции связаны правилом буравчика (рис.8.3).
– магнитная постоянная, μ – магнитная проницаемость среды (для вакуума μ=1). Направление тока и магнитной индукции связаны правилом буравчика (рис.8.3).
· Магнитная проницаемость среды μпоказывает, во сколько раз индукция магнитного поля в среде возрастает по сравнению с вакуумом:
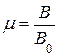 ,
,
где B – индукция магнитного поля в среде, B0 – в вакууме.
· Индукция магнитного поля в центре кругового витка с током I равна

и направлена по правилу правого винта (рис.8.4). Здесь R – радиус витка.
· Сила взаимодействия двух параллельных бесконечных проводников с токами I1 и I2, находящимися на расстоянии r, в расчёте на единицу длины проводника:
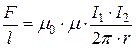 .
.
· Момент сил, действующий на контур с током в магнитном поле:
 ,
,
где В – индукция поля, pm – магнитный момент контура, α – угол между вектором 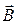 магнитной индукции и магнитным моментом
магнитной индукции и магнитным моментом 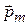 .
.
· Сила Лоренца (сила, действующая на заряд q, движущийся со скоростью  в магнитном поле с индукцией
в магнитном поле с индукцией 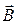 ):
):
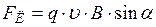 ,
,
 где a – угол, образованный вектором скорости
где a – угол, образованный вектором скорости  движущейся частицы и вектором
движущейся частицы и вектором 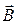 индукции магнитного поля.
индукции магнитного поля.
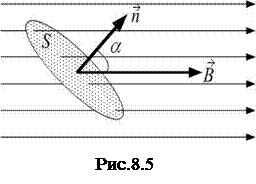
· Магнитный поток (поток вектора магнитной индукции В) через поверхность площадью S:
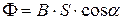 ,
,
где  – угол между вектором
– угол между вектором 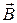 и нормалью
и нормалью 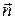 к поверхности (рис.8.5).
к поверхности (рис.8.5).
· Работа по перемещению контура с током в магнитном поле
A=I∙DФ,
где DФ – изменение магнитного потока, пронизывающего поверхность, ограниченную контуром; I – сила тока в контуре.
· Закон Фарадея (закон электромагнитной индукции): ЭДС индукции 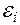 в замкнутом контуре равна по величине и противоположна по знаку скорости изменения магнитного потока
в замкнутом контуре равна по величине и противоположна по знаку скорости изменения магнитного потока 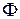 через поверхность, ограниченную контуром
через поверхность, ограниченную контуром
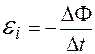 , точнее
, точнее  .
.
Если контур содержит N витков, то 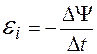 , или
, или 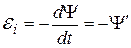 , где
, где  – полное потокосцепление.
– полное потокосцепление.
Частные случаи применения закона Фарадея:
а) разность потенциалов U на концах проводника длиной l, движущегося со скоростью u в однородном магнитном поле индукцией B:
U=B∙l∙u∙sina,
где a – угол между направлениями векторов скорости u и магнитной индукции В;
б) электродвижущая сила индукции 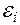 , возникающая в рамке, содержащей N витков, площадью S, при вращении рамки с угловой скоростью ω в однородном магнитном поле с индукцией В:
, возникающая в рамке, содержащей N витков, площадью S, при вращении рамки с угловой скоростью ω в однородном магнитном поле с индукцией В:
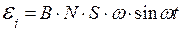 ,
,
где wt — мгновенное значение угла между вектором 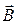 и вектором нормали
и вектором нормали 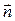 к плоскости рамки.
к плоскости рамки.
· Индуктивность контураLчисленно равна магнитному потоку Ф, пронизывающему контур, при единичной силе тока в контуре:
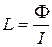 .
.
Для катушки с N витками 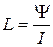 , где Ψ=NФ – полное потокосцепление.
, где Ψ=NФ – полное потокосцепление.
 · Индуктивность соленоида (рис.8.6):
· Индуктивность соленоида (рис.8.6):
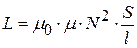 ,
,
где N – число витков, l – длина соленоида, S – площадь сечения соленоида.
· ЭДС самоиндукции 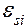 , возникающая в катушке с индуктивностью L, при изменении силы тока в ней:
, возникающая в катушке с индуктивностью L, при изменении силы тока в ней:
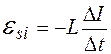 , или
, или  .
.
· Энергия магнитного поля контура с током:
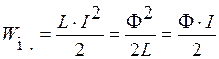 .
.
Для катушки с N витками 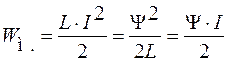 .
.
· Закон сохранения энергии для идеального колебательного контура:
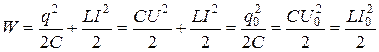 .
.
Дата добавления: 2014-10-31; просмотров: 393; Мы поможем в написании вашей работы!; Нарушение авторских прав |