Простейшая модель эпидемии

За многие годы существования человечества огромное число людей погибло от разных эпидемий. Для того чтобы уметь бороться с эпидемиями, т. е. своевременно проводить тот или иной комплекс мероприятий (прививки, вакцины, карантин и т.д.), необходимо уметь оценить эффективность каждого такого комплекса и выбрать наиболее оптимальный для данного вида эпидемии (холера, чума, грипп, СПИД и т.д.). Оценка эффективности базируется, как правило, на прогнозе о протекании эпидемии. Отсюда вытекает задача построения модели, которая могла бы служить целям прогноза. Самой простой моделью является описание естественного хода эпидемии без применения каких-либо профилактических мероприятий.

Итак, пусть имеется N здоровых людей, и в момент времени t = 0 в эту группу попадает один заболевший человек (источник инфекции). Предположим, что удаления заболевших из группы не происходит и человек становится источником инфекции сразу же, как заразился сам.

Обозначим через x(t) число источников инфекции в момент времени t, а через y(t) – число еще не заболевших (часть из них, естественно, может заболеть с течением времени). Очевидно, что х(t) + y(t) = N +1 в любой момент времени t, причем при t = 0 выполняется условие х(0) = 1. Рассмотрим интервал времени t, t +∆ t, где ∆ t достаточно мало. Естественно, что число больных ∆х, появившихся за этот интервал, пропорционально ∆t(∆x≈∆t). Естественно также предположить, что это число пропорционально числу контактов между больными и здоровыми, т.е. произведению x(t)y(t). Таким образом, ∆x≈αx(t)y(t)dt, где α – коэффициент пропорциональности. Устремляя ∆t к нулю из последнего соотношения, получим дифференциальное уравнение

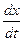=αx(t)(N+1-x(t)), (9.14)

которое вместе с начальным условием

х(0)=1 (9.15)

определяет функцию x(t). Уравнение (9.14) по виду является логистическим, оно рассмотрено в предыдущем параграфе. Поэтому сразу можно записать решение x(t) задачи Коши (9.14), (9.15) в удобном виде

, t 0. (9.16)

Итак, число заболевших – функция времени. Проанализируем эту функцию. Из уравнения (9.16) вытекает, что с течением времени число заболевших может только увеличиваться, а все здоровые люди заболеют, так как =N+1. Конечно, это грубая модель, не учитывающая естественного иммунитета у здоровых людей к данному заболеванию.

Интересно выяснить, как меняется скорость увеличения числа больных, т. е. величина

, t 0 (9.17)

Для решения этого вопроса нужно изучить величину .

Дифференцируя уравнение (9.17), получаем

, t 0. (9.18)

Из этого уравнения вытекает, что при > 0 при t и < 0 при

t . Следовательно, скорость возрастания заболевших – функция 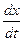– растет до момента t , а затем убывает. Несмотря на грубость модели, этот результат совпадает с экспериментальными данными: в начале эпидемии число заболевших резко возрастает, а впоследствии скорость распространения инфекции снижается.

Для сравнения приведем результаты использования более сложных моделей развития гриппозной эпидемии в Москве [22], где население составляет 8,5 млн человек. Это позволит нам также определить численные значения параметров N и α, при которых наша модель более реалистична.

Началу эпидемии соответствует число заболевших 79,1 тыс. человек, откуда N = 8,5 млн./79,1 тыс. ≈1100 человек. Пик заболеваемости приходится на 46-й день, т. е. 46 , откуда . По формуле (9.16) находим число больных . По отношению к 1100 чел. это составляет 11%, что согласуется с экспериментальными данными [22], где число больных равно 981 тыс. человек и составляет 11,5%. Конечно, применение соответствующих профилактических мер дает значительный положительный эффект, пик числа больных снижается с 981тыс. до 122 тыс. человек, однако создание соответствующей математической модели – существенно более трудная задача.