Случайные изменения среды

Рассмотрим теперь модель, учитывающую случайные изменения среды. Простейшая модель, соответствующая уравнению (10.1), имеет вид

(10.15)

N(0)=N₀, (10.16)

где y(t) – случайная величина со средним значением, равным нулю. Решение задачи (уравнения (10.15) при условии (10.16)) имеет вид

. (10.17)

Чтобы придать смысл интегралу от случайной величины y(t), сделаем некоторые упрощающие предположения. Будем считать, что y(t) – ступенчатая функция: y(t)=y_i, при i-1≤t≤i, i=1,2,.... при этом все случайные величины у, имеют нормальное распределение [6]. Нормальный закон распределения (часто называемый законом Гаусса) наиболее часто встречается на практике. Большинство встречающихся на практике случайных величин, таких, например, как ошибки измерений, могут быть представлены как суммы большого числа сравнительно малых слагаемых – элементарных ошибок, каждая из которых вызвана действием отдельной причины, не зависящей от остальных. Каким бы законам распределения ни были подчинены элементарные ошибки, особенности этих распределений в сумме большого числа слагаемых нивелируются, а сумма оказывается подчиненной закону, близкому к нормальному. Например, проводя измерения длины листьев, упавших с деревьев в лесу, мы имеем случайную величину Х – длину листьев. Вероятность того, что Х<х, т. е. Р={Х <х}, называется функцией распределения случайной величины и обозначается через F(x), а ее производная F'(x) = f(x) называется плотностью распределения и в случае нормального закона распределения имеет вид (рис. 10.1)

. (10.18)

Численные параметры т и σ – это математическое ожидание (среднее значение) и среднее квадратичное отклонение случайной величины X. Действительно,

Применяя замену переменной , получаем

(10.19)

Нетрудно убедиться, что первый из двух интегралов в уравнении (10.19) равен нулю, а второй представляет собой известный интеграл Эйлера–Пуассона

, (10.20)

поэтому из уравнения (10.19) вытекает, что М[Х]=т. Вычислим дисперсию величины X:

Применив снова замену переменной получим

(10.21)

Интегрируем это выражение по частям:

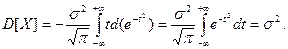(10.22)

Следовательно, σ в выражении (10.18) равна корню из дисперсии, т. e. среднему квадратичному отклонению. Итак,

Е[у_i]=т, D[y_i]=var(y_i)=σ². (10.23)

Покажем, что если т= , то Е 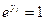. Действительно,

Применив снова замену х = , получим

(10.24)

Вернемся к формуле (10.17), которая в наших предположениях имеет вид

, (10.25)

откуда для среднего значения N(t) получаем выражение

, (10.26)

а для дисперсии D[N] = var(N) –

(10.27)

Теперь имеем

(10.28)

Следовательно,

(10.29)

и коэффициент вариации при t → ∞ равен

. (10.30)

Из формул (10.26) и (10.30) следует, что хотя, как и в детерминистском случае, среднее значение N(t) экспоненциально возрастает, экспоненциально возрастают и отклонения от среднего значения. Таким образом, с течением времени колебания численности популяции становятся все более резкими. В этом отражается то обстоятельство, что детерминистская система не имеет стационарного состояния, более того, при определенных соотношениях между а и σ вероятность ее вымирания приближается к единице.

Найдем вероятность вымирания популяции за время t – функцию p₀(t):

Положим , тогда у_t, имеет нормальное распределение, причем , vaz(y_t)=tσ². Следовательно,

Полагая , имеем

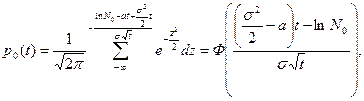(10.31)

где Ф(х) = 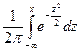– так называемый интеграл ошибок.

Если >0, т. e. σ²>2a, то → ∞ при t→ ∞, следовательно,

Проведенный анализ показывает, что преимущественное использование детерминистских, а не стохастических моделей оправдано лишь тем, что в математическом плане они проще и удобнее. При этом если детерминистская модель свидетельствует об устойчивом равновесии, то соответствующая стохастическая модель предсказывает длительное выживание; если же детерминистская модель не выявляет равновесия или предсказывает неустойчивое равновесие, то стохастическая модель может предсказать вероятность вымирания.

Контрольные задания

1. Допустим, вероятность λ рождения особью детеныша в два раза больше вероятности μ гибели самой особи. Определить среднее значение N(t) популяции в момент времени t = 100, вычислить также вариацию var (N(t)), коэффициент вариации , найти ограничения на λ и начальное значение популяции N₀, при котором коэффициент вариации при t = 100 будет меньше 0,1%.

2. В модели, учитывающей случайные изменения среды, будем предполагать, что а= . Найти соотношения между N₀ и σ, при которых вероятность вымирания популяции при t = 100 будет больше 90%. (Указание: воспользоваться таблицей значений интеграла вероятностей Ф(z), приведенной, например, в [6].)