Случайные процессы при описании популяций

Рассматриваемые выше модели – детерминистские. Это должно иметь какие-то основания, которые мы и попытаемся сейчас обсудить.

Если речь идет о динамике популяций, то можно выделить по крайней мере два аспекта, по которым детерминистская модель не может служить точным отражением реальной экологической системы: во-первых, она допускает бесконечно большую численность популяции; во-вторых, не учитывает случайных колебаний, происходящих в среде во времени.

В качестве примера детерминистской экологической модели рассмотрим уравнение

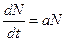, (10.1)

где N – число особей в момент времени t,

а – истинная скорость роста.

Решением этого уравнения, удовлетворяющим начальному условию

N(0)=No, (10.2)

является функция

N(t)=N₀e^at, (10.3)

(так называемый закон Мальтуса – закон роста популяции без конкуренции). В основе главного допущения здесь лежит то, что за короткий промежуток времени t каждая особь порождает aΔt новых особей.

В соответствующей стохастической модели принимается более правдоподобное допущение, согласно которому за период Δt одна особь с вероятностью λ производит одного потомка и с вероятностью μΔt умирает. Обозначим через р_i(t) вероятность того, что в момент времени t численность популяции равна i, i = 0, 1, 2, ... Рассмотрим величину p_i(t + Δt). В силу малости Δt можно считать, что численность популяции останется прежней, равной i, в результате трех независимых событий – появления потомков в популяции с численностью i–1, отсутствия случаев рождения и смерти в популяции с численностью i и смерти в популяции с численностью i+1. При этом вероятность p_i(t + Δt) равна сумме вероятностей этих событий:

p_i(t + Δt) = (i-1) λ p_i-1 (t) Δt+(1-i(λ+μ)p_i(t) Δt+(i+1) μ_i+1(t) Δt , откуда

(i-1) λ p_i-1 (t)- i(λ+μ)p_i(t)+ (i+1) μ_i+1(t).

Переходя в полученном соотношении к пределу при t → ∞, получим систему уравнений Колмогорова

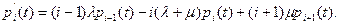(10.4)

В виде (10.4) уравнения справедливы при i= 2, 3, 4, .... При i = 1 из (10.4) получаем уравнение

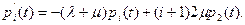(10.5)

а при i = 0 – уравнение

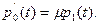(10.6)

(естественно считать, p_-1(t)≡0).

Если в начальный момент времени t=0 в популяции имелось N₀ особей, то начальные условия для системы обыкновенных дифференциальных уравнений с постоянными коэффициентами (10.4)–(10.6) имеют вид:

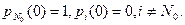(10.7)

Рассматриваемый процесс гибели и рождения является случайным процессом (классическим примером цепей Маркова [17]), а само решение задачи (10.4)–(10.7) можно получить стандартными методами теории обыкновенных дифференциальных уравнений (см., например, [47]). Нас интересуют следующие вероятностные характеристики: ожидаемое значение, т. е. среднее значение популяции в момент времени t

N(t)= 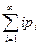(t) (10.8)

и вариация (дисперсия), т. е. среднее квадратичное отклонение от N(t)

. (10.9)

Для вычисления N(t) заметим, что из уравнения (10.5) и первого уравнения из (10.4) вытекает

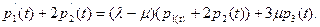
Продолжая этот процесс сложения, получим

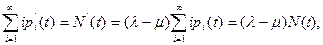
т. е. обыкновенное дифференциальное уравнение

N'(t)=(λ - μ)N(t) (10.10)

с начальным условием (10.7)

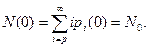(10.11)

Решение его, очевидно, равно

N(t)= 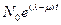, (10.12)

в частности, при λ > μ численность популяции экспоненциально возрастет (при λ=μ+a определяется уравнением (10.3)), а при λ < μ экспоненциально убывает при t → ∞. Аналогично (см. [17]) вычисляется вариация

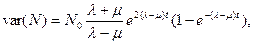(10.13)

откуда при λ > μ для коэффициента вариации получаем выражение

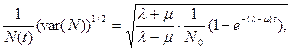(10.14)

которое при t → ∞ стремится к величине 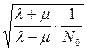. Следовательно, при достаточно больших начальных значениях популяции N₀ среднее квадратичное отклонение от N(t) является равномерно малым, и детерминистская модель дает адекватное представление о поведении популяции при больших значениях времени.