Пример 3. Применим метод простой итерации для решения системы уравнений

Применим метод простой итерации для решения системы уравнений

.

Заметим, что метод простой итерации сходится, так как выполняется условие преобладания диагональных элементов:

, ,

, .

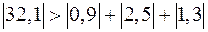Пусть требуемая точность . Вычисления будем проводить с четырьмя знаками после десятичной точки.

Приведем систему к виду:

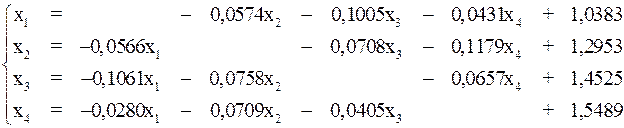
Величина равна 0,1179, т. е. выполняется условие и можно пользоваться критерием окончания итерационного процесса (8). В качестве начального приближения возьмем элементы столбца свободных членов: . Вычисления будем вести до тех пор, пока все величины 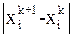, , а следовательно, и не станут меньше .

Последовательно вычисляем:

при

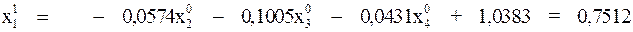
при

.

при

.

при

.

Вычисляем модули разностей значений при и :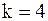

. Так как все они больше заданной точности 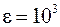, продолжаем итерации.

При

.

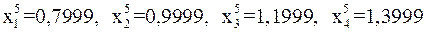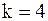Вычисляем модули разностей значений при и :

. Все они меньше заданной точности 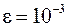, поэтому итерации заканчиваем. Приближенным решением системы являются следующие значения:

.

Для сравнения приведем точные значения переменных:

.