Сходимость метода

Теорема.Пусть в некоторой замкнутой окрестности 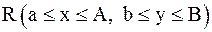имеется одно и толь­ко одно решение и приведенной системы.

Тогда если:

1) функции и определены и непрерывно дифференцируемы в ;

2) начальные приближения , и все последующие приближения , 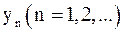при­над­лежат ;

3) в выполнены неравенства или

неравенства ,то процесс последовательных приближений сходится к решению , .

Оценка погрешности 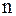-го приближения определяется неравенством:

,

где – наибольшее из чисел и , входящих в эти неравенства.

Сходимость метода считается хорошей, если ; при этом . Поэтому если в двух последовательных приближениях совпадают, например, три десятичных знака после запятой, то ошибка последнего приближения не превосходит 0,001.

Пример.Методом итерации решить систему с точностью до .