
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод скорейшего спуска решения нелинейных систем
Сущность метода скорейшего спуска заключается в том, что искомое решение системы  рассматривается как минимум некоторой функции
рассматривается как минимум некоторой функции  в
в 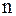 -мерном пространстве
-мерном пространстве 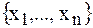 , и этот минимум ищется в направлении, противоположном направлению градиента функции
, и этот минимум ищется в направлении, противоположном направлению градиента функции  , то есть в направлении скорейшего убывания этой функции. Фунция
, то есть в направлении скорейшего убывания этой функции. Фунция  связана с функциями
связана с функциями 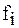 исходной системы соотношениями:
исходной системы соотношениями:
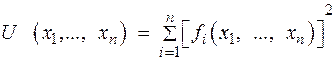 .
.
Пусть точка  является начальным приближением к искомому решению. Через эту точку проводится поверхность уровня
является начальным приближением к искомому решению. Через эту точку проводится поверхность уровня  , а также нормаль к данной поверхности, которая указывает направление скорейшего убывания функции
, а также нормаль к данной поверхности, которая указывает направление скорейшего убывания функции  . Точка, в которой нормаль касается новой поверхности уровня
. Точка, в которой нормаль касается новой поверхности уровня  , будет следующим приближением к исходному решению. Нормаль, проведенная к этой поверхности через точку
, будет следующим приближением к исходному решению. Нормаль, проведенная к этой поверхности через точку 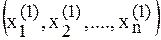 , даёт возможность дойти до точки
, даёт возможность дойти до точки  , в которой нормаль касается какой-то другой поверхности
, в которой нормаль касается какой-то другой поверхности  , и т. д.
, и т. д.
Так как 
 , где
, где  то последовательность точек
то последовательность точек  ,
, 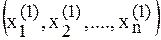 ,
,  … приведет к минимальному значению функции
… приведет к минимальному значению функции  , т. е. к искомому решению исходной системы.
, т. е. к искомому решению исходной системы.
Последовательные приближения определяются из матричного равенства  , где через
, где через  обозначен вектор в
обозначен вектор в 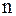 -мерном пространстве, указывающий координаты точки
-мерном пространстве, указывающий координаты точки  , т. е. значение
, т. е. значение  -го приближения;
-го приближения;  – параметр, характеризующий изменение функции
– параметр, характеризующий изменение функции  вдоль соответствующей нормали,
вдоль соответствующей нормали,  – градиент функции
– градиент функции  в точке
в точке  .
.
В общем случае параметр  может быть найден из уравнения:
может быть найден из уравнения:
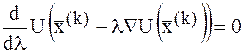 , (1)
, (1)
где 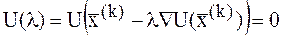 – скалярная функция, определяющая изменение функции
– скалярная функция, определяющая изменение функции  . При этом берется наименьший положительный корень уравнения (1).
. При этом берется наименьший положительный корень уравнения (1).
Если считают  малой величиной и не учитывают членов, содержащих
малой величиной и не учитывают членов, содержащих  во второй и высших степенях, то приближенно искомое решение можно найти из матричных равенств
во второй и высших степенях, то приближенно искомое решение можно найти из матричных равенств  ,
,  ,
,  , где
, где
 ,
,
 ,
,
 .
.
Важным достоинством метода скорейшего спуска является его неизбежная сходимость. Поэтому его рекомендуется применять для уточнения решения в тех случаях, когда другие итерационные методы расходятся.
Пример. Методом скорейшего спуска приближенно вычислить корни системы: 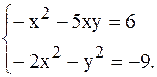
Решение.Пусть  .
.
Здесь  и
и  .
.
Подставляя нулевое приближение, будем иметь
 ,
, 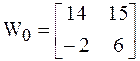 ,
,  ,
,  ,
,  ,
,
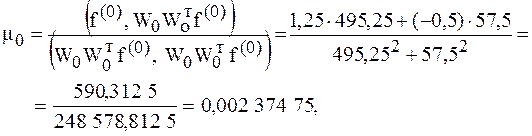
 .
.
Вычислим  .
.
Аналогично найдем второе приближение 
 .
.
Тогда  .
.
Для контроля вычислим невязку: 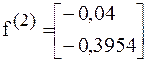 и так далее.
и так далее.
Получаем решение системы: 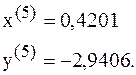
Дата добавления: 2015-01-05; просмотров: 274; Мы поможем в написании вашей работы!; Нарушение авторских прав |