Вычисление собственных значений матрицы Методом Данилевского

Сущность метода Данилевского заключается в том, что исходная матрица А:

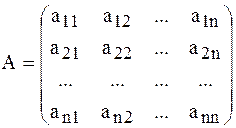
после преобразования подобия приводится к матрице Фробениуса Р:

,

то есть , где – неособенная матрица. Так как подобные матрицы обладают одинаковыми характеристическими полиномами, то имеем:

.

Вначале нужно строку привести в строку . Предполагая, что , разделим все элементы – го столбца матрицы А на . Тогда её 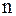-ая строка примет вид

.

Затем вычтем - й столбец преобразованной матрицы, умноженный соответственно на числа , из всех остальных ее столбцов.

В результате получим матрицу, последняя строка которой имеет желаемый вид 0 0 … 1 0.

Произведя те же операции над единичной матрицей, получим матрицу

,

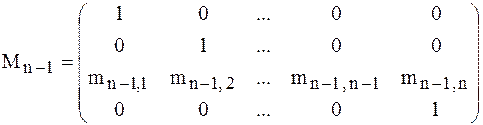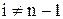где при . (1)

. (1')

Эти операции равносильны умножению справа матрицы на матрицу А.

, (2)

где при ,

при . (2')

Для подобия матриц нужно умножить полученную матрицу на слева: .

Очевидно, обратная матрица имеет вид

.

Обозначим , то есть

,

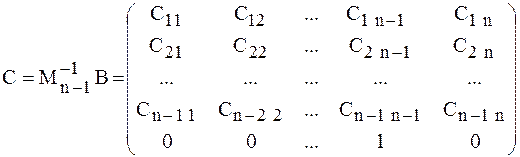где (3)

при , (3')

то есть полученная матрица С подобна матрице А.

Продолжая этот процесс, получим матрицу Фробениуса.

,

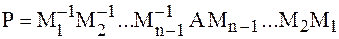если все промежуточных преобразований возможны.

Пример. Привести к виду Фробениуса матрицу:

.

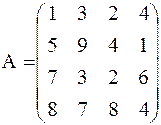Решение.Вычисления будем располагать в таблице 4. В строках 1–4 помещаем элементы данной матрицы и контрольные суммы в . Элемент . В строке I записываем элементы третьей строки матрицы , вычисляемые по формулам (1), (1'):

, ,

, .

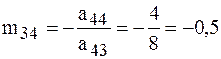Сюда же помещаем элемент 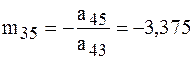. Число -3,375 должно совпасть с элементами строки I , не входящими в контрольный столбец (после замены элемента на -1).

В строках 5–8 в графе выписываем третью строку матрицы , которая совпадает с четвертой строкой исходной матрицы А. В строках 5–8 в соответствующих столбцах выписываем элементы матрицы , вычисляемые по формулам (2), (2'):

Преобразованные элементы третьего столбца получаются с помощью умножения исходных элементов на 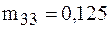. Например,

Таблица 4

Номер строки		Столбцы матрицы	Σ	Σ/
				8
I		-1	-0,875	0,125 -1	-0,5	-3,375
		-1	1,25	0,25		3,5	3,25
			5,5	0,5	-1	6,0	5,5   11,25
			1,25	0,25		11,5
7/			58,5	11,5
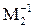
II		-0,67	0,017 -1	-0,127	-0,97	-2,83
		-1,8333	0,021	0,004	1,782	-0,026	-0,047
10	58,5	-2,666	0,094	-0,5811	-6,3589	-9,512	-9,606
	11,5
10/		-227,4597	17,818	23,16165	-302,4	-488,966
III		0,0044	0,0783	0,1	-1,3298	-2,14
	-227,45	0,008	-0,1226	-0,1827	4,22	3,9228	3,91148
17,818
23,16165
-302,497
				-261	-960

Соответственно, последняя строка матрицы В имеет вид (0 0 1 0). Для контроля пополним матрицу В преобразованными по аналогии элементами:

Полученные результаты записываем в столбце Σ^/ . Прибавив к ним элементы третьего столбца, будем иметь контрольные суммы:

для строк 5–8 (столбец Σ) .

Преобразование , произведенное над матрицей В и дающее матрицу , изменяет лишь третью строку матрицы В, то есть седьмую строку таблицы. Элементы строки 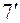получаются по формулам (3), ( 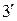) . Например:

.

Те же преобразования проводим над столбцом Σ:

.

В результате получаем матрицу С, состоящую из строк 5, 6, 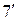, 8 с контрольными суммами Σ. Далее, приняв матрицу С за исходную и выделив элемент , продолжим процесс аналогичным образом.

Таким образом, матрица Фробениуса имеет вид

Отсюда, решая уравнение , найдем собственные значения исходной матрицы.

6. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЁННЫХ ИНТЕГРАЛОВ.
МЕТОД СИМПСОНА (МЕТОД ПАРАБОЛ)

Заменим график функции на отрезке , , 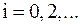, параболой, проведенной через точки , , где 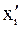– середина отрезка . Эта парабола есть интерполяционный многочлен второй степени с узлами . Нетрудно убедиться, что уравнение этой параболы имеет вид:

,

где .

Проинтегрировав эту функцию на отрезке , получим

.

Суммируя полученные выражение по , получим квадратурную формулу Симпсона (или формулу парабол):

.

Оценка погрешности.Для оценки погрешности формулы Симпсона воспользуемся следующей теоремой.

Теорема.Пусть функция имеет на отрезке непрерывную производную четвертого порядка 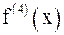. Тогда для формулы Симпсона справедлива следующая оценка погрешности: , где

.

Замечание.Если число элементарных отрезков, на которые делится отрезок , четно, т.е. , то параболы можно проводить через узлы с целыми индексами, и вместо элементарного отрезка длины 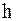рассматривать отрезок длины . Тогда формула Симпсона примет вид: , а вместо последней оцен­ки будет справедлива следующая оценка погрешности:

.