Описание установки. Теория метода

Электромагнитной индукцией называется возникновение электродвижущей силы (ЭДС) в проводнике под действием магнитного поля. ЭДС электромагнитной индукции равна скорости изменения магнитного потока со временем с обратным знаком (закон электромагнитной индукции):

В лабораторной работе проверяется прямая пропорциональная зависимость ЭДС электромагнитной индукции от скорости изменения магнитного потока.

Лабораторная работа выполняется на установке, принципиальная схема которой изображена на рис. 5.1.

Рис. 5.1

В качестве контура , создающего магнитное поле, используются либо катушки Гельмгольца (КГ) – при проверке закона электромагнитной индукции, либо исследуемый контур с током – при изучении магнитного поля проводников с током (упражнение 2).

Катушки Гельмгольца представляют две короткие по длине последовательно соединенные одинаковые соосные катушки с одинаковым числом витков , расположенные на расстоянии, равном радиусу катушек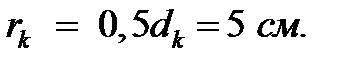

Контур питается от генератора (ГСФ) пилообразным током (рис. 5.2,а).

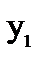С сопротивления , включенного последовательно с контуром , напряжение подается на вход (канал 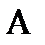) осциллографа.

По закону Ома сила тока

поэтому наблюдаемая на экране осциллографа зависимость напряжения

от времени соответствует зависимости силы тока от времени в контуре . Более того, численные значения и совпадают, ибо .

Рис. 5.2

ЭДС индуцируется в эталонном датчике (ДЭ), представляющем собой катушку малого диаметра = 0,02 м с числом витков , и находящемся в магнитном поле контура .

Индуцируемая в датчике ЭДС определяет напряжение 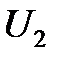на концах катушки датчика, которое подается на вход осциллографа (канал Б).

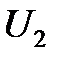На экране осциллографа можно одновременно наблюдать зависимости напряжения , связанного с силой тока в контуре , и напряжения , связанного с индуцируемой в датчике ЭДС от времени (рис. 5.2,б).

По определению магнитный поток через поперечное сечение датчика (через площадь ограниченную одним витком датчика)

где - угол между нормалью к и магнитной индукцией .

Магнитный поток через площадь, ограниченную всеми витками датчика (поток сцепления катушки), больше в раз:

При данном угле изменение магнитного потока

Тогда ЭДС индукции, возникающей в датчике, по величине будет равна

и проверка зависимости от сводится к проверке зависимости от скорости изменения индукции магнитного поля, вызывающего электромагнитную индукцию, .

Из закона Био-Савара-Лапласа следует, что для всех проводников с током

Коэффициент пропорциональности называется калибровочным коэффициентом; он показывает, насколько изменяется индукция магнитного поля контура с током при изменении силы тока в нем на 1 А:

Тогда

и проверка зависимости от сводится к проверке зависимости от скорости изменения силы тока в контуре .

При линейной зависимости силы тока от времени (в течение каждого полупериода при

пилообразном токе) скорость изменения силы тока со временем , равная тангенсу угла наклона графика зависимости 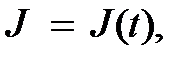постоянна. Поэтому:

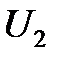1) если положение датчика ДЭ не изменяется , то при пилообразном токе в контуре в датчике возникает постоянная во времени ЭДС электромагнитной индукции и пилообразному току в контуре соответствует прямоугольная форма графика зависимости ЭДС и напряжения от времени, приведенная на рис. 5.2,б.

2) для промежутка времени скорость изменения силы тока можно выразить через конечные изменения силы тока и времени т.е.

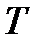где и 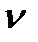- период и частота колебаний тока.

Тогда для ЭДС индукции, возникающей в датчике под действием магнитного поля контура при пилообразном токе в нем, получаем формулу

Отсюда следует, что проверка закона электромагнитной индукции (5.1) сводится к проверке зависимостей:

1) при неизменных частоте пилообразного тока и ориентации датчика

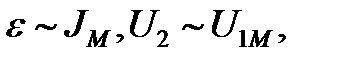
т.е. чем больше амплитуда пилообразного тока в катушках Гельмгольца, тем большая ЭДС индукции должна возникнуть в эталонном датчике;

2) при неизменных амплитуде пилообразного тока и ориентации датчика

т.е. чем больше частота пилообразного тока в катушках Гельмгольца, тем большая ЭДС индукции должна возникнуть в эталонном датчике;

3) при неизменных частоте и амплитуде пилообразного тока

т.е. с увеличением угла между нормалью к сечению катушки и магнитной индукцией ЭДС индукции изменяется прямо пропорционально косинусу угла ;

4) при неизменных частоте и амплитуде пилообразного тока и ориентации датчика ЭДС индукции постоянна.

В лабораторной работе проверяется цепочка зависимостей:

при выбранных и .

В условиях опыта равна напряжению , которое подается на осциллограф, а измеряется напряжение , равное 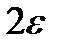(рис. 5.2,б).

Частота , напряжение , численно равное , угол измеряются в лабораторной работе.

Калибровочный коэффициент 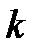можно определить на основе опытных данных, используя расчетную формулу (5.5):

Калибровочный коэффициент можно определить также теоретически, учитывая, что катушки Гельмгольца короткие и рассматривая их как круглые проводники с током. На оси катушек на расстояниях и 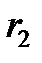от них модуль индукции магнитного поля равен сумме индукций магнитного поля катушек:

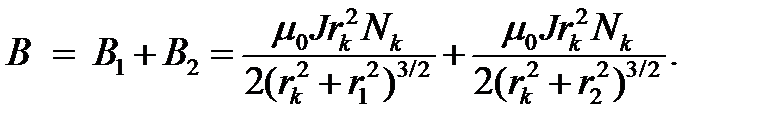
Эталонный датчик, в котором возникает ЭДС индукции, располагается посередине между катушками, а из-за малости его диаметра можно принять, что он находится в точке на расстояниях 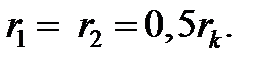Тогда

и для калибровочного коэффициента посередине между катушками получим выражение