КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Механические колебания. 1 страница
| Номер опыта | l | Dl | I | DI | U | DU | R | DR | sR |
| ... | |||||||||
Порядок обработки результатов следующий:
1) по результатам измерений диаметра проволоки рассчитать среднее значение 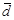 . Определить среднюю абсолютную Dd и среднюю квадратическую sd погрешности измерения диаметра по формулам (3) и (4) соответственно;
. Определить среднюю абсолютную Dd и среднюю квадратическую sd погрешности измерения диаметра по формулам (3) и (4) соответственно;
2) используя полученные данные для тока и напряжения, вычислить значения сопротивлений R. Среднее значение R не вычислять, так как это не имеет физического смысла;
3) вычислить погрешности косвенного измерения сопротивления DR и sR по формулам (5) и (6) для какого-либо одного значения R. Считать, что sI = DI и sU = DU;
4) построить график зависимости R = f(l). Экспериментальные точки нанести на координатную плоскость, откладывая по оси х величину l, а по оси у соответствующее ей значение сопротивления R. Для каждой точки указать погрешности Dl и DR. Для этого каждую точку изобразить как пересечение двух отрезков длиной 2Dl вдоль оси х и 2DR вдоль оси у с центрами, соответствующими измеренным значениям;
5) определить графически среднее значение удельного сопротивления
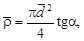
где  ;
;
6) вычислить погрешности Dr и sr результатов косвенного определения удельного сопротивления, используя формулы (7) и (8) соответственно. В этих формулах в качестве I и U использовать значения какого-либо одного измерения (при определенном значении длины  );
);
7) результаты измерения удельного сопротивления представить в виде 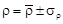 и
и 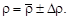
| |
Контрольные вопросы
1. Какие измерения называют прямыми?
2. Чему равна абсолютная, относительная и средняя квадратическая ошибки прямых измерений?
3. Какие измерения называют косвенными?
4. Чему равна максимальная абсолютная, относительная и средняя квадратическая ошибки косвенных измерений?
5. Как определить погрешности, вносимые различными измерительными приборами?
6. Что такое класс точности прибора?
| |
Работа 2. ЭКВИВАЛЕНТНОСТЬ ГРАВИТАЦИОННОЙ
И ИНЕРТНОЙ МАСС
Цель работы – изучить законы равноускоренного движения, динамики поступательного движения связанных тел; определить ускорение свободного падения тел различной массы.
Общие сведения
Масса – одна из основных характеристик материи, являющаяся мерой ее инертных и гравитационных свойств. Инертная масса фигурирует во втором законе динамики. Гравитационная масса характеризует силу, с которой тела притягиваются друг к другу, и представлена в законе всемирного тяготения. Ответ на вопрос, различаются ли инертная и гравитационная массы, может дать только опыт.
Покажем, что инертная и гравитационная массы пропорциональны друг другу. Сила тяготения, действующая на тело с гравитационной массой mг,
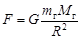 ,
,
где G – гравитационная постоянная; Mг – гравитационная масса Земли; R – расстояние между центрами материальных точек mг и Mг.
C другой стороны, согласно второму закону динамики, эта сила
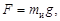
где  – инертная масса;
– инертная масса; 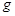 – ускорение свободного падения.
– ускорение свободного падения.
Соответственно
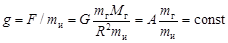 ,
,
где А = GMг/R2 = const.
Экспериментально установлено, что ускорение свободного падения одинаково для всех тел. Из этого следует, что mг и mи пропорциональны друг другу. А соответствующим выбором G можно отношение mг / mи привести к единице.
|
Равенство инертной и гравитационной масс, экспериментально подтвержденное с относительной погрешностью 10-12, лежит в основе принципа эквивалентности гравитационных сил и сил инерции. Простейший опыт по проверке сказанного заключается в установлении равенства ускорения свободного падения для всех тел.
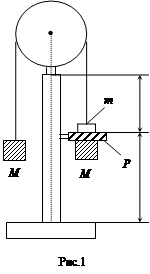
Измерение ускорения свободного падения тел различной массы проводится на приборе Атвуда. Через ролик, смонтированный на подшипнике таким образом, чтобы он мог вращаться с возможно малым сопротивлением, проходит нитка с двумя одинаковыми грузами массой М каждый (рис.1). Система находится в равновесии.
Если по одну сторону блока прибавить небольшой грузик m, то система, состоящая из больших грузов М и малого m, получит ускорение, с которым пройдет путь S1. Дополнительный груз на кольце Р отцепляется и далее грузы М пройдут путь S2 с постоянной скоростью.
Полагая, что сила трения в системе, масса ролика и нити пренебрежимо малы, а нить нерастяжима, можно показать, что ускорение на участке S1
 . (1)
. (1)
С другой стороны, считая начальную скорость равной нулю, можно записать
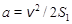 , (2)
, (2)
где v – скорость в конце движения на участке S1.
Приравняв правые части выражений (1) и (2), получим
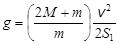 .
.
Так как v = S2/t, где t – время движения с постоянной скоростью на участке S2, то окончательно
 . (3)
. (3)
Видно, что, для определения g необходимо измерить время движения с постоянной скоростью на участке S2 известных масс М и m при фиксированных значениях S1 и S2.
|
Общий вид прибора Атвуда показан на рис.2. На вертикальной колонке 7, закрепленной на основании 9, находятся три кронштейна: неподвижный нижний кронштейн 8 и два подвижных (средний 15 и верхний 16), а также верхняя втулка 17. Основание оснащено регулируемыми ножками 10 для выравнивания положения прибора. На верхней втулке при помощи верхнего диска 4 закреплен узел подшипника ролика 5, ролик 18 и электромагнит 6. Через ролик проходит нить 14 с привязанными к ее концам грузами 3 и 12.
Электромагнит после подведения к нему питающего напряжения при помощи фрикционной муфты удерживает систему ролика с грузами в состоянии покоя.
Верхний и средний кронштейны можно перемещать вдоль колонки и фиксировать в любом положении, устанавливая, таким образом, длину пути равномерно-ускоренного (S1) и равномерного (S2) движений. Для облегчения измерения S1 и S2 на колонку нанесена миллиметровая шкала (13), все кронштейны имеют указатель положения, а верхний кронштейн – дополнительную черту, облегчающую точное согласование нижней грани большего груза с точкой начала движения.
На среднем кронштейне закреплен кронштейн 2 и фотоэлектрический датчик 19. Кронштейн 2 снимает с падающего вниз большого груза дополнительный груз, а фотоэлектрический датчик в это время создает электрический импульс, сигнализирующий о начале равномерного движения системы грузов. Оптическая ось фотоэлектрического датчика (черта на его корпусе) находится на уровне указателя положения среднего кронштейна.
Нижний кронштейн оснащен двумя кронштейнами 1 с резиновыми амортизаторами, в которые ударяют завершающие свое движение грузы. На этом кронштейне закреплен также фотоэлектрический датчик 20 с оптической осью на уровне указателя положения кронштейна. После пересечения этого уровня нижней гранью падающего груза образуется электрический сигнал о прохождении грузами определенного пути.
В основании прибора находится блок 11, включающий миллисекундомер, к которому подключены фотоэлектрические датчики, а также подводится напряжение, питающее обмотку электромагнита.
Порядок выполнения работы
1. Измерить при помощи шкалы на колонке заданные пути равноускоренного (S1) и равномерного (S2) движений большого груза.
2. На правый большой груз положить один из дополнительных грузов.
3. Измерить время движения большого груза на пути S2.
4. Повторить измерения 10 раз и определить среднее значение времени движения большого груза на пути S2:
 ,
,
где n = 10; 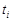 – результат i-го измерения.
– результат i-го измерения.
5. Повторить измерения с грузами другой массы и вычислить по формуле (3) ускорение свободного падения каждого использованного груза, фиксируя результаты в табличной форме:
| Номер опыта | m | S1 | S2 | ti | 
| g | sg |
| … | |||||||
| n |
6. Рассчитать стандартное отклонение
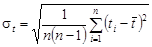
и сравнить полученное значение с приборной ошибкой. Если приборная ошибка мала, ею можно пренебречь.
7. Вычислить погрешность измерения ускорения свободного падения
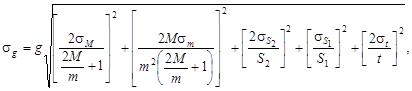
где  = sm = 0,01 г;
= sm = 0,01 г;  =
= 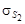 = ±1 мм; st £ 10-3 с.
= ±1 мм; st £ 10-3 с.
Контрольные вопросы
1. Как отношение масс m/M влияет на погрешность в определении времени падения t?
2. Почему масса m не может быть как угодно малой?
3. Почему измеренное на данной установке ускорение свободного падения меньше, а не больше 9,8 м/с2?
4. От каких параметров зависит ускорение движения грузов на участке S1? на участке S2?
Работа 3. Изучение законов механики
с помощью прибора атвуда
Цель работы – экспериментально проверить законы динамики поступательного и вращательного движения, кинематические уравнения равномерного и равноускоренного движений; измерить момент инерции, силу трения и момент силы трения с помощью прибора Атвуда.
Общие сведения
Путь S и скорость v тела, движущегося прямолинейно с постоянным ускорением a без начальной скорости, изменяются со временем согласно уравнениям
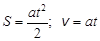 . (1)
. (1)
Исключая из уравнений (1) время, получим связь координаты и скорости в виде
 . (2)
. (2)
При равномерном прямолинейном движении путь, скорость и время связаны уравнением
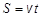 .
.
Движение точки по окружности характеризуется угловой скоростью 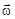 , угловым ускорением
, угловым ускорением 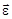 , а также тангенциальным
, а также тангенциальным 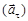 и нормальным
и нормальным 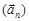 ускорениями. Линейная скорость v связана с угловой соотношением v = wR, а тангенциальное и угловое ускорения – соотношением аt = eR.
ускорениями. Линейная скорость v связана с угловой соотношением v = wR, а тангенциальное и угловое ускорения – соотношением аt = eR.
Основными законами динамики являются законы Ньютона. Второй закон Ньютона определяет причину изменения движения:
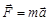 ,
,
где 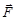 – сила, вызывающая движение тела; m – масса тела;
– сила, вызывающая движение тела; m – масса тела;  – ускорение тела.
– ускорение тела.
|
Если тело движется под действием нескольких сил, равнодействующую силу находят как векторную сумму сил:
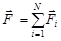 .
.
Основное уравнение динамики вращательного движения твердого тела имеет вид
 ,
,
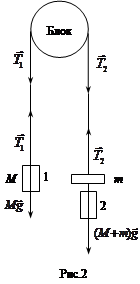 где
где  – результирующий момент сил,
– результирующий момент сил, 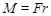 ; r – плечо силы, т.е. кратчайшее расстояние от оси до линии действия силы; J – момент инерции тела относительно оси вращения; e – угловое ускорение.
; r – плечо силы, т.е. кратчайшее расстояние от оси до линии действия силы; J – момент инерции тела относительно оси вращения; e – угловое ускорение.
Устройство и работа прибора Атвуда описаны в работе 2. Оценим количественно движение системы грузов (рис.1) на участках S1 (равноускоренное движение) и S2 (равномерное движение). Пусть М – масса грузов 1 и 2, m – масса перегруза. Уравнение движения грузов и блока (рис.2) запишем в виде
 ;
;
 ;
;
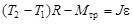 ,
,
где Т1 и Т2 – силы натяжения, создаваемые грузами 1 и 2 соответственно; R и J – радиус и момент инерции блока; 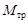 – момент силы трения, действующей на ось блока.
– момент силы трения, действующей на ось блока.
Ускорения грузов а1 = а2 = а, так как нить считается нерастяжимой. Пренебрегая проскальзыванием нити по блоку, можно положить 
Решив систему уравнений относительно ускорения а, получим
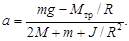 (3)
(3)
Если допустить, что силы трения в блоке пренебрежимо малы по сравнению с mg, то Мтр/R « mg. Если пренебречь массой блока, от которой зависит момент инерции J, то J/R2 « 2M + m. Тогда
 .
.
Если, наконец, масса перегруза значительно меньше масс грузов (m « 2M), то ускорение можно рассматривать как линейную функцию массы перегруза:
a = mg/(2M). (4)
График зависимости a = f(m), соответствующий формуле (4), представляет собой прямую, проходящую через начало координат.
Справедливость упрощающих предположений, приводящих от формулы (3) к формуле (4), можно проверить экспериментально, измерив ускорение для различных масс грузов. Если график зависимости a = f(m), построенный по экспериментальным данным, будет сильно отличаться от графика, построенного по теоретической формуле (4), то это будет означать, что сделанные упрощающие предположения не совсем правильны. В этом случае можно из экспериментальных данных определить момент силы трения, силу трения и момент инерции блока.
Чтобы найти силу трения Fтр, следует определить сначала момент силы 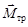 . Для этого запишем выражение (3), содержащее неизвестные J и
. Для этого запишем выражение (3), содержащее неизвестные J и 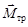 , для двух пар значений а и m:
, для двух пар значений а и m:
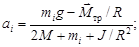

где i и k – индексы, обозначающие порядковый номер измерения.
Решив эту систему относительно J и 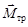 , получим
, получим
|


Сила трения
Fтр = 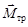 /r, (6)
/r, (6)
где r – радиус оси блока.
Чтобы определить ускорение грузов на участке S1, воспользуемся уравнением (2):
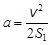 .
.
На участке S2 груз движется равномерно со скоростью 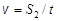 , следовательно,
, следовательно,
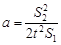 . (7)
. (7)
Измерения проводятся на приборе Атвуда (см. работу 2). В этом приборе имеется два одинаковых груза с массами М, соединенными нитью, перекинутой через блок. На прaвый груз добавляется перегруз массой m, после чего система приходит в равноускоренное движение и проходит путь S1. В конце этого пути перегруз автоматически снимается, и система начинает двигаться равномерно на пути S2.
Результатом экспериментальной части работы должны стать значения времени t прохождения грузом 2 пути S2.
К установке прилагается набор из нескольких колец (перегрузов) с разными массами m. Используя эти кольца по отдельности или в комбинации друг с другом, можно получить достаточно большой набор масс перегрузов.
Порядок выполнения работы
1. Надеть на груз 2 перегруз (одно или несколько колец).
2. Измерить время t прохождения грузом пути S2.
3. Повторить измерение времени t с перегрузом той же массы не менее 5 раз.
4. Повторить пп.2 и 3 для всех остальных перегрузов.
5. Записать значения S1 и S2; оценить погрешность их определения по шкале, нанесенной на колонке прибора Атвуда.
6. Рассчитать величину ускорения для всех масс перегрузов: экспериментальное значение по формуле (7), теоретическое (aт) по формуле (4).
7. Результаты измерений и расчетов записать по форме:
| Номер опыта | m | S1 | S2 | t | Dt | a | Da | aт | |
| … | |||||||||
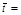
| 
| 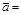
| 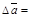
| 
| |||||
8. Вывести самостоятельно формулу для расчета Da, учитывая, что а измеряется косвенно через прямые измерения t, S1 и S2, абсолютные погрешности которых известны.
9. Построить графики зависимости a = f(m) по экспериментальным данным и по теоретической формуле (4).Сравнить вид получившихся графиков и сделать вывод относительно справедливости законов механики, лежащих в основе соотношения (4).
10. Если графики сильно отличаются друг от друга (экспериментальный график не проходит через начало координат), взять две пары значений а и m (не соседние) и рассчитать момент инерции блока J, момент силы трения в блоке Мтр по формулам (5), силу трения в блоке Fтр по формуле (6). Массы грузов 1 и 2 M = (60,0±0,5) г.
Контрольные вопросы
1. Каковы законы изменения во времени пути и скорости точки, движущейся равномерно и равноускоренно по прямолинейной траектории?
2. Как связаны линейная скорость и нормальное ускорение с угловой скоростью? Каково соотношение тангенциального и углового ускорений при движении точки по окружности?
3. Сформулируйте основные законы динамики поступательного и вращательного движения.
4. Какой характер имеет движение груза в приборе Атвуда на различных участках траектории? Чем определяется это различие?
5. Какой вид должна иметь кривая зависимости ускорения грузов от массы перегруза? Какой физический смысл имеют точки пересечения этой кривой с осями координат? При каких условиях кривая a(m) близка к прямой?
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Основное уравнение динамики вращательного движения твердого тела
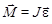 ,
,
где  – суммарный момент внешних сил, приложенных к телу относительно оси вращения; J – момент инерции тела относительно той же оси;
– суммарный момент внешних сил, приложенных к телу относительно оси вращения; J – момент инерции тела относительно той же оси; 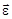 – угловое ускорение.
– угловое ускорение.
В динамике вращательного движения различают два понятия: момент силы относительно точки и момент силы относительно оси вращения.
Момент силы относительно точки О определяется как векторное произведение
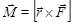 ,
,
где 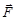 – сила;
– сила; 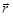 – радиус-вектор, проведенный из точки О в точку приложения силы.
– радиус-вектор, проведенный из точки О в точку приложения силы.
Момент силы относительно оси вращения есть проекция  на произвольную ось z, которая проходит через точку О:
на произвольную ось z, которая проходит через точку О:
 ,
,
где l – плечо силы, т.е. кратчайшее расстояние от оси до линии действия силы.
|
Момент инерции тела является мерой инертности тела при вращательном движении, подобно тому, как масса тела является мерой инертности тела при поступательном движении. Момент инерции тела зависит от распределения массы тела относительно оси вращения. Для вычисления момента инерции твердого тела относительно данной оси разобьем мысленно тело на большое число малых элементов объема dV – материальных точек (см. рисунок). Тогда момент инерции элемента объема dV относительно оси вращения ОО'
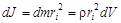 ,
,
а полный момент инерции тела
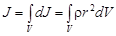 ,
,
где dm = rdV – масса элемента объема dV; ri – расстояние до оси вращения; r – плотность вещества в элементе объема dV.
Таким образом, задача нахождения момента инерции тела относительно оси вращения сводится к интегрированию.
Следует подчеркнуть, что момент инерции не зависит ни от момента внешних сил  , ни от углового ускорения.
, ни от углового ускорения.
Для расчетов моментов инерции относительно произвольной оси может быть использована теорема Штейнера. Согласно ей, момент инерции J относительно произвольной оси равен сумме момента инерции тела Jc относительно оси, проходящей через центр инерции тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
Дата добавления: 2014-10-31; просмотров: 321; Мы поможем в написании вашей работы!; Нарушение авторских прав |