
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Механические колебания. 5 страница
Порядок выполнения работы
1. Подставить стаканчик под кран, открыть его и, дождавшись, когда вода начнет вытекать каплями, зафиксировать по шкале начальную высоту уровня воды в сосуде Н1 и одновременно включить секундомер.
2. Измерить по шкале уровни воды h1 и h2 в коленах манометра.
3. Когда уровень воды в сосуде уменьшится приблизительно на 5 см, перекрыть кран, остановить секундомер, записать время t вытекания воды и конечную высоту уровня воды в сосуде Н2.
4. Повторить 5 раз пп.1-3.
5. Измерить температуру T воздуха в комнате и атмосферное давление pат.
6. Результаты измерений оформить в виде таблицы:
| Номер опыта | h1 | h2 | H1 | H2 | t | T | pат | r | l |
| … |
7. Вычислить Dр по формуле (5), объем воздуха, вошедшего в сосуд через капилляр (равный объему вытекшей воды), по формуле (6).
8. По результатам эксперимента вычислить коэффициент вязкости газа по формуле (2), найти длину свободного пробега молекул газа и эффективный диаметр молекул газа по формулам (3) и (4) соответственно.
9. Рассчитать средние арифметические погрешности измерений.
Контрольные вопросы
1. В чем заключается явление вязкости?
2. Что такое длина свободного пробега и эффективный диаметр молекул идеального газа?
3. Как длина свободного пробега и эффективный диаметр молекул зависят от давления газа?
4. Что такое коэффициент вязкости (внутреннего трения)?
5. В какой части экспериментальной установки и почему существенную роль играет вязкость воздуха?
6. В чем сущность закона Пуазейля?
| |
Работа 13. определение коэффициента
вязкости жидкости
Цель работы – определить коэффициент вязкости жидкости методом Стокса.
Общие сведения
Механизмы вязкости в газах (см. работу 12) и жидкостях существенно отличаются вследствие неодинаковой структуры этих сред. В жидкостях расстояние между молекулами значительно меньше, чем в газах. Поэтому на движение молекул в жидкостях, в первую очередь, влияет межмолекулярное взаимодействие, ограничивая их подвижность. Вязкость жидкостей значительно больше, чем у газов и уменьшается с ростом температуры (у газов наоборот).
Пусть в заполненном жидкостью сосуде движется шарик, размеры которого значительно меньше размеров сосуда (см. рисунок). Слой жидкости, прилегающий к шарику, движется со скоростью шарика. Соседние слои движутся с меньшими скоростями и, следовательно, между слоями жидкости возникают силы внутреннего трения. Дж.Г.Стокс показал, что эта сила при малых значениях скорости пропорциональна скорости движения шарика v и его радиусу r:
|
 , (1)
, (1)
где h – коэффициент вязкости, зависящий от рода жидкости и от температуры.
На шарик действуют три силы: сила тяжести шарика  , направленная вниз, сила внутреннего трения
, направленная вниз, сила внутреннего трения  и выталкивающая сила
и выталкивающая сила  , направленные вверх (см. рисунок). Шарик сначала падает ускоренно, но затем действующие силы очень быстро уравновешиваются:
, направленные вверх (см. рисунок). Шарик сначала падает ускоренно, но затем действующие силы очень быстро уравновешиваются:
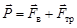 , (2)
, (2)
так как с увеличением скорости растет и сила трения. Движение становится равномерным.
Сила тяжести  , где m – масса шарика; g – ускорение свободного падения. Так как m = rV, где r – плотность материала шарика; V – его объем, то
, где m – масса шарика; g – ускорение свободного падения. Так как m = rV, где r – плотность материала шарика; V – его объем, то
 . (3)
. (3)
Выталкивающая сила по закону Архимеда
 , (4)
, (4)
где  – плотность жидкости.
– плотность жидкости.
Таким образом, формулу (2) с учетом выражений (1), (3) и (4) можно переписать в виде
 ,
,
откуда
 . (5)
. (5)
Эта формула, называемая формулой Стокса, справедлива для случая, когда шарик падает в среде, простирающейся безгранично по всем направлениям. Достичь этого в лаборатории практически невозможно, поэтому приходится учитывать размеры сосуда, в котором падает шарик.
Если шарик падает вдоль оси цилиндрического сосуда радиусом R, то формула (5) преобразуется к виду
 . (6)
. (6)
В лабораторной установке r « R, поэтому в качестве расчетной можно пользоваться формулой (5).
Установка для проведения эксперимента представляет собой большой цилиндрический сосуд с исследуемой жидкостью. Вдоль образующей цилиндра через каждые 20 см нанесены горизонтальные штрихи.
Порядок выполнения работы
1. Измерить при помощи микроскопа диаметр шарика d.
2. Через отверстие в крышке прибора опустить шарик в жидкость.
3. Измерить секундомером время t прохождения шариком участка пути, на котором скорость падения шарика постоянна.
4. Повторить пп.1-3 с другими шариками.
5. Определить температуру жидкости T, при которой производились измерения (она равна температуре окружающей среды).
6. Результаты измерений оформить в виде таблицы:
| Номер опыта | Т | rж | r | d | r | t | l | v | h | Dh |
| … |
7. Подставив измеренные и известные величины в формулу (5), вычислить коэффициент вязкости hi для каждого шарика и среднюю квадратическую погрешность измерений
 ,
,
где n – число измерений с данной жидкостью, n = 10.
При малом числе измерений следует вывести формулу средней арифметической погрешности Dh и вычислить ее.
Контрольные вопросы
1. Каков физический смысл коэффициента вязкости и его размерность?
2. В чем сущность закона Стокса?
3. Какие силы действуют на шарик при его движении в жидкости? Как эти силы зависят от времени?
4. Как изменяются скорость и ускорение движения шарика в зависимости от времени?
5. Чем обусловлено введение поправки 2,1 r/R в уравнение (6)?
6. Какие факторы влияют на скорость шарика?
| |
Работа 14. определение коэффициента
поверхностного натяжения жидкости
Цель работы – определить коэффициент поверхностного натяжения воды при комнатной температуре по капиллярному подъему.
Общие сведения
Над свободной поверхностью жидкости находится ее пар. Плотность пара во много раз меньше плотности жидкости. Поэтому молекула поверхностного слоя окружена меньшим числом молекул, чем молекула, находящаяся внутри жидкости. Силы, действующие на молекулу поверхностного слоя со стороны молекул жидкости и пара, не уравновешиваются, и результирующая сила направлена внутрь жидкости. Для перевода молекулы жидкости изнутри в поверхностный слой необходимо совершить работу против этой силы, за счет чего увеличивается запас потенциальной энергии молекул поверхностного слоя жидкости. Любая система в состоянии равновесия имеет минимальную потенциальную энергию. Жидкость может уменьшить свою потенциальную энергию за счет уменьшения площади поверхности. Следовательно, существуют силы, стремящиеся сократить поверхность жидкости. Эти силы и называют силами поверхностного натяжения. Они направлены по касательной к поверхности жидкости. Чтобы увеличить поверхность жидкости, надо совершить работу против сил поверхностного натяжения:
 , (1)
, (1)
где a – коэффициент пропорциональности, называемый коэффициентом поверхностного натяжения.
Коэффициент a является одной из основных величин, характеризующих свойства жидкости. Если  = 1, то, как следует из формулы (1), a = DА, т.е. коэффициент поверхностного натяжения определяется работой, необходимой для увеличения площади поверхности жидкости на единицу. Коэффициент поверхностного натяжения в СИ имеет размерность джоуль на квадратный метр (Дж/м2).
= 1, то, как следует из формулы (1), a = DА, т.е. коэффициент поверхностного натяжения определяется работой, необходимой для увеличения площади поверхности жидкости на единицу. Коэффициент поверхностного натяжения в СИ имеет размерность джоуль на квадратный метр (Дж/м2).
С повышением температуры коэффициент поверхностного натяжения жидкости уменьшается, и при критической температуре, когда исчезает различие между жидкостью и ее паром, a = 0.
Можно показать, что если сила взаимодействия между молекулами жидкости меньше силы взаимодействия этих молекул с молекулами вещества, из которого изготовлен сосуд, то поверхность жидкости будет вогнутой (смачивание); при обратном соотношении поверхность будет выпуклой (несмачивание). В результате искривления поверхности появляется добавочное давление Dр. Согласно формуле Лапласа
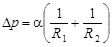 , (2)
, (2)
где R1 и R2 – радиусы кривизны двух взаимно перпендикулярных сечений поверхности жидкости.
Искривление поверхности особенно заметно в очень узких трубках – капиллярах. Для цилиндрических капилляров формула (2) принимает вид
 ,
,
где R – радиус сферической поверхности, при полном смачивании или несмачивании практически равный радиусу капилляра.
Если стеклянный капилляр опустить в широкий сосуд с водой, то вследствие смачивания поверхность воды в капилляре станет вогнутой, возникнет добавочное давление Dp, которое в данном случае будет отрицательным по сравнению с атмосферным, т.е. будет направлено вверх. Поэтому результирующее давление в капилляре станет меньше, чем в широком сосуде и жидкость в капилляре начнет подниматься выше уровня ее в широком сосуде. По мере подъема жидкости будет возникать гидростатическое давление рг, создаваемое этим столбиком жидкости и направленное вниз: pг = rgh.
Жидкость в капилляре будет подниматься до тех пор, пока гидростатическое давление столбика жидкости высотой h не уравновесит добавочное давление, вызванное кривизной поверхности: pг = Dр. Соответственно  Поэтому, зная h, можно определить a.
Поэтому, зная h, можно определить a.

|
Если над уровнем воды в капилляре создать давление Dр1, добавочное по сравнению с давлением воздуха на воду в широком сосуде, то уровень воды в капилляре понизится и сравняется с уровнем воды в сосуде. При этом добавочное давление Dр1 воздуха будет равно добавочному давлению Dp, вызванному кривизной поверхности.
Добавочное давление воздуха измеряется по разности уровней h жидкости в коленах манометра: Dp1 = rgh, где r – плотность жидкости в манометре; g – ускорение свободного падения. Следовательно, 2a/R = rgh, откуда
 . (3)
. (3)
Величину подъема h жидкости в капилляре можно было бы измерить непосредственно, но это неудобно. В работе для определения h используется простая установка с манометром (см. рисунок). Капилляр, опущенный в стакан K с водой, трубкой В сообщается с более широкой трубкой D и манометром С. Трубка D опущена в сосуд с водой, установленный на столике, который можно закрепить в любом положении винтом Е. Поднимая столик, мы сжимаем воздух в трубках В и D, и в капилляре над поверхностью воды создается добавочное давление Dp1, измеряемое U-образным манометром (М).
Чтобы измерить диаметр капилляра, его укрепляют на штативе и помещают перед объективом микроскопа так, чтобы в поле зрения был торец капилляра. Изображение канала капилляра должно накладываться на изображение шкалы окуляра. Диаметр капилляра измеряют в делениях шкалы (цена деления указана).
Порядок выполнения работы
1. Измерить диаметр капилляра микроскопом.
2. Вставить капилляр с пробкой в трубку В установки и погрузить нижний конец капилляра на 1-2 мм в воду (вода в капилляре установится выше уровня воды в стакане).
3. Поднимая столик E, опускать уровень воды в капилляре до тех пор, пока не появится и не оторвется первый пузырек воздуха.
4. Измерить разность h1 уровней жидкости в манометре.
5. Повторить опыт 3 раза.
6. Вычислить добавочное давление воздуха в капилляре h = h1 – h', где h' – превышение уровня воды в стакане над нижним концом капилляра, h' = 1-2 мм.
7. Повторить пп.1-4 с капиллярами других диаметров.
8. Результаты опыта оформить в виде таблицы:
| Номер опыта | d | R | DR | h | Dh | a |
| … |
9. Вычислить для каждого капилляра коэффициент поверхностного натяжения a по формуле (5), а затем среднее значение  .
.
10. Вычислить среднюю арифметическую погрешность Da.
11. Результаты измерений представить в виде 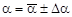 .
.
Контрольные вопросы
1. Чем обусловлена энергия поверхностного слоя жидкости?
2. Какова физическая природа сил поверхностного натяжения? Как они направлены?
3. Что такое коэффициент поверхностного натяжения? От чего он зависит и в каких единицах измеряется?
4. Что такое добавочное (лапласово) давление? От чего оно возникает? Как его рассчитывают?
5. Почему при смачивании жидкость в капиллярах поднимается, а при несмачивании опускается? От чего зависит высота подъема жидкости в капиллярах?
рекомендательный библиографический список
1. Детлаф А.А. Курс физики / А.А.Детлаф, Б.М.Яворский. М.: Высшая школа, 2000.
2. Савельев И.В. Курс физики. М.: Высшая школа, 1998. Т. 1- 3.
3. Трофимова Т.И. Курс физики. М.: Наука, 2003.
4. Яворский Б.М. Справочник по физике / Б.М.Яворский, А.А.Детлаф. М.: Наука, 1998.
| |
содержание
Обработка результатов измерений в физическом практикуме............................ 3
Погрешности прямых измерений.................................................................. 4
Погрешности косвенных измерений.............................................................. 6
Правила представления результатов измерений.......................................... 9
Правила построения графиков....................................................................... 9
Динамика поступательного движения.................................................................... 11
Работа 1. Оценка точности прямых и косвенных измерений...................... 11
Работа 2. Эквивалентность гравитационной и инертной масс..................... 17
Работа 3. Изучение законов механики с помощью прибора Атвуда.......... 22
Динамика вращательного движения....................................................................... 28
Работа 4. Определение моментов инерции параллелепипеда методом крутильных колебаний 31
Работа 5. Определение момента инерции с помощью маятника Обербека 35
Работа 6. Определение момента инерции твердых тел с помощью маятника Максвелла 39
Работа 7. Измерение скорости полета пули с помощью баллистического маятника 43
Работа 8. Определение ускорения свободного падения при помощи универсального маятника 48
Работа 9. Изучение прецессии гироскопа...................................................... 55
Молекулярная физика............................................................................................. 60
Работа 10. Определение отношения теплоемкости воздуха при постоянном давлении к теплоемкости при постоянном объеме методом адиабатического расширения......................................................................... 60
Работа 11. Определение отношения теплоемкости воздуха при постоянном давлении к теплоемкости при постоянном объеме методом стоячей волны................................................................................................. 66
Работа 12. Определение коэффициента вязкости, длины свободного пробега и эффективного диаметра молекул газа 71
Работа 13. Определение коэффициента вязкости жидкости........................ 77
Работа 14. Определение коэффициента поверхностного натяжения жидкости 81
Рекомендательный библиографический список..................................................... 85
* Коэффициент Пуассона – отношение теплоемкости воздуха при постоянном давлении Ср к теплоемкости при постоянном объеме CV.
* Гидростатическое давление выражается через разность уровней: p = rgh, где r – плотность жидкости. В итоговую формулу давления войдут в виде отношения, поэтому сомножитель rg можно опустить с самого начала.
Механические колебания.
1. Собственные колебания.
Собственными называются свободные колебания, возникающие в колебательной системе в отсутствие сил сопротивления (трения).
Колебания в подобной системе описываются уравнением вида
 , (1)
, (1)
а сама система называется гармоническим осциллятором.
Примерами гармонических осцилляторов могут служить пружинный, математический и физический маятники (Рис. 1).



Рис. 1
Пружинный маятник – тело массой m, прикрепленное к пружине с жесткостью k.
Математический маятник – материальная точка, подвешенная на невесомой нерастяжимой нити длиной l.
Физический маятник – тело, совершающее колебания относительно оси О, находящейся на расстоянии l от его центра инерции С.
Для математического и физического маятников роль величины x в уравнении (1) играет угол отклонения j от положения равновесия. При этом гармоническими являются только малые колебания маятников.
Дата добавления: 2014-10-31; просмотров: 334; Мы поможем в написании вашей работы!; Нарушение авторских прав |
