Механические колебания. 2 страница

В общем случае расчет момента инерции представляет собой достаточно сложную задачу, и часто он определяется экспериментально с помощью основного уравнения динамики вращательного движения, методом крутильных колебаний и др.

Момент импульса материальной точки определяется как векторное произведение:

,

где m – масса материальной точки; – ее скорость; 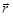– расстояние от точки до оси вращения.

Момент импульса материальной точки

L = mvr.

Момент импульса твердого тела, вращающегося вокруг некоторой оси,

,

где J – момент инерции тела; w – угловая скорость вращения.

Закон сохранения момента импульса в замкнутой системе формулируется следующим образом: суммарный момент импульса всех тел замкнутой системы остается постоянным .

Кинетическая энергия вращающегося тела

.

Цель работы – определить моменты инерции прямоугольного параллелепипеда относительно трех взаимно перпендикулярных осей, проходящих через центр масс, с помощью крутильных колебаний.

Общие сведения

Пусть тело представляет собой однородный прямоугольный параллелепипед со сторонами а, b, с (см. рисунок). Моменты инерции этого тела относительно соответствующих осей

;

;

.

Здесь оси х, у и z проходят через центр масс перпендикулярно граням со сторонами bс, ас и аb соответственно.

Если тело имеет форму куба, то a = b = c и

.

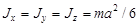В данной работе момент инерции определяется методом крутильных колебаний. Если тело, висящее на нерастяжимой нити (так, что направление нити проходит через центр тяжести тела), повернуть в горизонтальной плоскости на некоторый угол a, то в результате деформации нити возникнет упругая сила. Она создаст крутящий момент (момент силы) (здесь D – модуль кручения нити подвеса), возвращающий систему в исходное состояние. В результате возникнут крутильные колебания.

Из теории крутильных колебаний следует, что период колебаний

. (1)

где J – момент инерции.

Так как D неизвестен, для его исключения из формулы (1) следует провести измерения периода колебаний с телом, момент инерции которого относительно оси вращения или легко рассчитывается, или известен. Таким телом может быть, например, куб, момент инерции которого .

В экспериментальной установке предусмотрена рамка для закрепления различных тел, отличающихся массой и размерами.

Пусть J₀, J_р, и J – моменты инерции куба, рамки и параллелепипеда относительно некоторой оси. Тогда на основании формулы (1) можно записать

(2)

где Т_р – период колебаний рамки; Т₀ – период колебаний рамки и куба; Т – период колебаний рамки и параллелепипеда.

Исключая из уравнений (2) D и J_р, получим

. (3)

Экспериментальная установка состоит из массивного основания со штативом. Кронштейны на штативе служат для закрепления стальной проволоки, на которой подвешена рамка. На среднем кронштейне закреплена стальная плита, являющаяся основанием для фотоэлектрического датчика, электромагнита и шкалы. Положение электромагнита относительно фотоэлектрического датчика указано стрелкой на шкале. Во время колебаний крутильного маятника стрела рамки прерывает световой поток, в результате чего в электронной схеме генерируются импульсы, которые после усиления подаются на электронный секундомер.

Порядок выполнения работы

1. Включить установку.

2. Нажатием кнопки «ПУСК» включить электромагнит, который должен удержать рамку прибора.

3. Нажать последовательно кнопки «СБРОС» и «ПУСК», измерить время t десяти колебаний пустой рамки; вычислить период колебания Т = t/N, где N – число колебаний.

4. Повторить измерения не менее 10 раз и вычислить среднее значение t.

5. Установить в рамку куб и повторить пп.2-3 не менее 10 раз.

6. Установить в рамку параллелепипед и повторить пп.2-3 не менее 10 раз (период колебаний параллелепипеда измерить для трех взаимно перпендикулярных осей).

7. Результаты измерений оформить в виде таблицы:

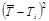
Номер опыта	t	T			m	sm	a	sa
…

8. Обработать результаты измерений. Вычислить момент инерции куба

где m – масса куба, m = 0,962 кг; а – длина ребра куба, а = 5,0 см.

Зная средние значения периодов, по формуле (3) рассчитать , 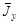и .

Вычислить средние квадратические ошибки для всех измеренных периодов по формуле

где n – число измерений; – среднее значение соответствующего периода колебаний; – значение периода в i-м опыте.

Вычислить среднюю квадратическую ошибку момента инерции куба по формуле

где – ошибка при измерении массы, = 2 г; – приборная ошибка, = 1 мм.

Рассчитать средние квадратические ошибки 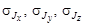для моментов инерции параллелепипеда относительно осей х, у, z. Так как Т » Т_р и Т₀ » Т_р, то формулу для вычисления погрешности можно записать в виде

,

где – средние квадратические ошибки.

Расчеты погрешностей следует провести для всех трех моментов инерции. Окончательные результаты представить в виде .

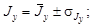
Контрольные вопросы

1. В чем заключается физический смысл момента инерции? От чего зависит момент инерции?

2. В чем сущность метода крутильных колебаний?

3. Какие параметры влияют на период колебаний крутильного маятника?

4. Почему Т и Т₀ много больше Т_р?

5. Как рассчитать J₀?

6. Почему у параллелепипеда J_x ¹ J_y ¹ J_z,, а у куба J_x = J_y = J_z?

Работа 5. Определение момента инерции с помощью маятника Обербека

Цель работы – исследовать зависимость момента инерции крестовины с грузами от распределения массы относительно оси вращения, проходящей через центр масс.

Общие сведения

Маятник Обербека состоит из крестовины, на стержнях которой находятся грузы. Они могут перемещаться по стержням и закрепляться в нужном положении (см. рисунок). Крестовина с грузами насажена на вал, на котором укреплены два шкива различного радиуса. На шкив намотана нить, которая переброшена через блок.

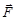К концу нити подвешивают груз массой m, под действием силы тяжести которого система приводится в движение. На груз действует сила тяжести и сила натяжения , поэтому на основании второго закона Ньютона можно записать

(1)

где g – ускорение свободного падения; а – ускорение, с которым движется груз.

Крестовина приходит во вращательное движение под действием момента силы натяжения

; = Fr₀, (2)

где J – момент инерции относительно оси вращения; e – угловое ускорение; r₀ – радиус шкива.

Из уравнений (1) и (2) получим

. (3)

Так как угловое ускорение связано с ускорением а соотношением e = а/r₀, то формула (3) принимает вид

, (4)

где а = 2h/t²; h – путь, пройденный грузом за время t.

Таким образом, с учетом формулы (4) получим

. (5)

Порядок выполнения работы

1. Убедиться, что две неподвижные рамки установлены на вертикальной линейке на расстоянии 40-50 см друг от друга. Измерить радиус шкива r₀.

2. Установить грузы на стержнях на максимальном расстоянии от оси вращения и закрепить их.

3. Включить установку, нажав кнопку «ПУСК».

4. Не отпуская кнопку «ПУСК» нажать кнопку «СБРОС» и намотать нить на шкив, установив подвешенный груз на уровне верхней рамки выше оптической оси фотоэлектрического датчика.

5. Закрепить груз, нажав кнопку «ПУСК» и обнулить счетчик нажатием кнопки «СБРОС».

6. Опустить груз, отключив электромагнит нажатием кнопки «ПУСК», измерить время t его движения до оптической оси нижней рамки. Взять не менее трех отсчетов t и вычислить .

7. Сместить грузы на стержнях на два деления к центру и повторить пп.4-6, измерить расстояние r от оси вращения до центра масс груза.

8. Повторить измерения для 8-10 положений грузов.

9. Записать результаты экспериментов в табличной форме:

Номер опыта	r	t		Jэ	Jр
…

Экспериментальные значения момента инерции J_э рассчитать по формуле (5).

10. Обработать результаты измерений. Из теоретических соображений следует, что момент инерции крестовины с четырьмя грузами массой , если считать грузы материальными точками, можно выразить формулой

(6)

где J₀ – момент инерции крестовины без грузов.

Из формулы (6) следует, что J = f(r²). Следовательно, если построить график этой функции, то должна получиться прямая, продолжение которой будет пересекать ось ординат в некоторой точке, соответствующей J₀. Такое построение можно сделать приближенно, «на глаз». Однако математические методы обработки результатов наблюдений позволяют сделать такое построение достаточно точным. Легче всего сделать это с помощью метода наименьших квадратов. Суть этого метода состоит в том, что из всех возможных прямых линий надо взять такую, для которой сумма квадратов отклонений каждой точки от прямой будет наименьшей.

Для удобства перепишем формулу (6) в виде

, (7)

где r² = х и = K. Согласно методу

(8)

где ; N – число опытов; J_i – экспериментальное значение момента инерции J_э, полученное для каждого опыта.

Обработку результатов эксперимента удобно вести в табличной форме:

Номер опыта	ri	xi	Ji		xiJi
…

Рассчитав J₀ и K по формулам (8), следует построить зависимость J_р от x по формуле (7). Так как через две точки можно провести только одну прямую, то для построения этой прямой можно взять какие-нибудь две удобные точки. Далее по формуле (7) рассчитать момент инерции J_p для каждого опыта, заполняя последний столбец (см. п.9).

Среднее квадратическое отклонение

.

11. По данным опыта и расчетов построить график функции в координатах J – r², предварительно обработав данные опыта методом наименьших квадратов, и вычислить доверительный интервал измерения момента инерции в границах .

Контрольные вопросы

1. Что такое момент инерции? От чего он зависит? Как можно рассчитать момент инерции относительно оси вращения?

2. Каков физический смысл основного уравнения динамики вращательного движения? Что такое момент силы?

3. Как выглядит график зависимости момента инерции в координатах J – r² и J – r? Почему результаты опыта лучше обрабатывать в координатах J – r²?

4. Почему график зависимости J = f(r²) не проходит через начало координат? Какой смысл имеет величина J₀?

5. Какой смысл имеет тангенс угла наклона графика к горизонтальной оси?

Работа 6. определение момента инерции

твердых тел с помощью маятника максвелла

Цель работы – изучить устройство маятника Максвелла и определить с его помощью момент инерции твердых тел.

Общие сведения

Маятник Максвелла представляет собой однородный диск С, через центр которого проходит металлический стержень D (рис.1). К концам этого стержня прикреплены две нити. Они тщательно, виток к витку, наматываются на стержень в направлении от его конца к диску. При освобождении маятника возникает поступательное движение вниз и вращательное вокруг оси симметрии. Вращение, продолжаясь по инерции в низшей точке движения (когда нити уже размотаны), приводит вновь к наматыванию нити на стержень, диск поднимается, и движение снова повторяется, т.е. возникают колебания.

Выведем расчетную формулу для момента инерции маятника на основе закона сохранения энергии. Когда маятник поднят на высоту h, его полная энергия состоит только из потенциальной энергии E_п = mgh. В наинизшем положении маятника E_п = 0, а полная энергия равна сумме кинетических энергий поступательного и вращательного движений:

.

Из закона сохранения энергии следует, что полная энергия маятника в верхнем и нижнем положениях должна быть одинакова, т.е.

.

Отсюда момент инерции

(1)

Поскольку поступательное движение маятника возникает только за счет вращательного, то угловая (w) и линейная (v) скорости связаны соотношением

. (2)

Подставив уравнение (2) в (1), получим

. (3)

Для равнопеременного движения связь между h, v и t может быть записана в виде

.

Подставив выражение для v в формулу (3), получим окончательно

. (4)

Формулу (4) можно было бы вывести и на основе уравнений динамики для поступательного и вращательного движения.

В основании 1 установки (рис.2) закреплена колонка 8, к которой прикреплен неподвижно верхний кронштейн 9 и подвижный нижний кронштейн 7. На верхнем кронштейне находится электромагнит 10 и фотоэлектрический датчик 11, а на нижнем кронштейне – фотоэлектронный датчик 3.

Маятник представляет собой диск 5, закрепленный на оси 6, подвешенной на двух нитях 4 (бифилярный подвес). На диск можно насаживать сменные коль­ца 12, изменяя таким образом момент инерции системы.

Маятник удерживается в верхнем положении электромагнитом 10. Фотоэлектрические датчики 3 и 11 соединены с электронным секундомером 2. Верхний электронный датчик задает момент начала движения маятника, а нижний – момент окончания движения (опускания) маятника.

Порядок выполнения работы

1. Надеть на диск маятника одно из колец (если оно не надето).

2. Включить установку. Нижний край кольца маятника должен быть примерно на 2 мм ниже оптической оси фотоэлектрического датчика, ось маятника должна быть горизонтальной.

3. Намотать на ось маятника нить подвески до фиксации маятника в верхнем положении электромагнитом.

4. Измерить время падения маятника по прибору.

5. Повторить пп.3-4 еще 10 раз.

6. Провести измерения с другими кольцами.

7. По измеренным значениям времени определить среднее значение времени падения маятника

.

8. По шкале на вертикальной колонке прибора измерить длину маятника h.

9. Измерить радиусы оси (R_о), диска (R_д) и колец (R_к).

10. Записать массы оси (m_о), диска (m_д) и колец (m_к), вычислить общую массу маятника . Результаты измерений и вычислений зафиксировать в табличной форме:

11. Обработать результаты эксперимента. Вычислить экспериментальное и теоретическое значение момента инерции маятника

; ,

где J_о – момент инерции оси маятника, ; J_к – момент инерции кольца, надетого на диск, ; J_д – момент инерции диска, ; R_д и R_к – радиусы диска и кольца соответственно.

Для полученного экспериментально значения момента инерции вычислить среднюю квадратическую погрешность

.

Погрешность измерения времени s_t определить по результатам измерений (s_t = Dt), погрешность массы s_m принять равной 1 г, погрешности s_h и оценить по цене деления используемых измерительных приборов.

12. Записать окончательный результат в форме , сравнить экспериментальное значение J с теоретическим J_т.

Контрольные вопросы

1. Что такое момент инерции материальной точки?

2. Что такое момент инерции твердого тела?

3. От чего зависит величина момента инерции твердого тела?

4. Каков принцип действия маятника Максвелла?

5. Какие силы вызывают поступательное движение маятника?

6. Момент каких сил вызывает вращательное движение маятника?

7. Вывести формулу для определения момента инерции с помощью маятника Максвелла.

Работа 7. измерение скорости полета пули с помощью баллистического маятника

Цель работы – определить скорость полета пули с помощью крутильных колебаний баллистического маятника.

Общие сведения

Скорость полета пули может достигать значительной величины, поэтому ее прямое измерение, т.е. определение времени, за которое пуля проходит известное расстояние, требует специальной аппаратуры. Разработаны и косвенные измерения скорости полета пули. Можно, например, использовать явление неупругого соударения.

Если летящая пуля испытывает неупругий удар с неподвижным телом большей массы, их скорость после удара будет существенно меньше первоначальной скорости пули и ее можно будет измерить достаточно простыми методами, например, с помощью крутильных колебаний баллистического маятника, представляющего собой два стержня 1, подвешенных на вертикально натянутой проволоке 3 (рис.1). На стержнях закреплены мисочки с пластилином 2 и перемещаемые грузы 4. При попадании пули в мисочку с пластилином, маятник начинает поворачиваться вокруг своей вертикальной оси. Если пренебречь силами трения можно воспользоваться законами сохранения.

На основании закона сохранения момента импульса можно написать

, (1)

где m – масса пули; v – ее скорость; l – расстояние от оси вращения маятника до точки удара пули; w – угловая скорость маятника; J – момент инерции маятника.

Согласно закону сохранения механической энергии при повороте кинетическая энергия маятника переходит в потенциальную энергию закручивающейся проволоки:

, (2)

где – наибольший угол поворота маятника; D – модуль кручения проволоки.

Из уравнений (1) и (2) можно получить

. (3)

Так как момент инерции пули существенно меньше момента инерции маятника J, то выражение (3) можно привести к виду

Тогда скорость пули

. (4)