Механические колебания. 3 страница

Модуль кручения проволоки D определим, измерив период крутильных колебаний маятника Т. Так как при малых углах отклонения , то

. (5)

Подставив выражение (5) в уравнение (4), найдем

. (6)

Для определения J измерим периоды колебаний маятника Т₁ и Т₂ при различных положениях грузов. Из формулы (5) следует

. (7)

Момент инерции маятника

,

где М – масса одного неподвижного груза; R – расстояние от центра масс груза до оси вращения; J₀ – момент инерции маятника без грузов.

Для различных положений грузов, т.е. различных расстояниях от центра масс груза до оси вращения R₁ и R₂:

откуда

. (8)

Решая систему уравнений (7) и (8), найдем

(9)

Запишем формулу (6) для положения грузов R₁:

и, подставив вместо J₁ выражение (9), получим окончательно расчетную формулу

. (10)

Общий вид баллистического маятника показан на рис.2. В основании 2, снабженном регулирующими ножками 1, позволяющими выравнивать прибор, закреплена колонка 3 с тремя кронштейнами: верхним (8), средним (4) и нижним (14). К кронштейну 4 прикреплено стреляющее устройство 9, прозрачный экран с нанесенной на него угловой шкалой 10 и фотоэлектрический датчик 12. Кронштейны 4 и 8 имеют зажимы, служащие для крепления стальной проволоки 13, на которой подвешен маятник, состоящий из двух мисочек 6, наполненных пластилином, двух перемещаемых грузов 7, двух стержней 5 и «водилки» 11. Фотоэлектрический датчик соединен разъемом с привинченным к основанию миллисекундомером.

Порядок выполнения работы

1. Установить максимальное расстояние между грузами и измерить R₁.

2. Зарядить пулей стреляющее устройство и произвести выстрел.

3. Измерить максимальный угол отклонения a_max маятника.

4. Повторить 3 раза пп.2, 3 и найти среднее значение a_max.

5. Включить установку.

6. Отклонить маятник на угол a_max и отпустить его; измерить время 10 колебаний и вычислить период Т₁. Повторить измерения периода 5 раз.

7. Установить минимальное расстояние между грузами и измерить R₂.

8. Отклонить маятник на угол a_max и отпустить его; измерить время 10 колебаний и вычислить период Т₂. Повторить измерения периода 5 раз.

9. Результаты эксперимента оформить в виде таблицы:

10. Рассчитать скорость пули по формуле (10), подставив значение a_max в радианах.

11. Вывести самостоятельно формулу для расчета Dv и вычислить абсолютную погрешность. Погрешность DT определить по результатам измерений периода, погрешность DR и Da – по цене деления измерительных приборов, погрешность DM принять равной 1 г.

12. Записать результат для скорости пули в виде

Контрольные вопросы

1. Что такое баллистический маятник?

2. От каких параметров установки зависит период колебаний баллистического маятника?

3. От чего зависит амплитуда колебаний баллистического маятника?

4. При каких упрощающих предположениях выведена формула (9)?

5. Можно ли пользоваться формулой (9), если удар пули о мишень происходит под углом, отличным от прямого?

свободного падения при помощи

универсального маятника

Цель работы – определить ускорение свободного падения с помощью универсального маятника.

Общие сведения

Наиболее точные измерения ускорения свободного падения выполняются с помощью косвенных методов. Многие из них основаны на использовании формул для периода колебаний математического и физического маятников.

Математическим маятником называется материальная точка, подвешенная на невесомой, нерастяжимой нити и совершающая колебание в вертикальной плоскости под действием силы тяжести. Достаточно хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити.

Период колебаний математического маятника

, (1)

где l – длина маятника; g – ускорение свободного падения.

Ускорение g можно вычислить, измерив Т и l. Погрешность определения g в этом случае связана с тем, что реальный маятник, используемый в лабораторных условиях, может только с некоторым приближением рассматриваться как математический (чем больше l, тем точнее измерения).

Физическим маятником называется абсолютно твердое тело, совершающее колебания под действием силы тяжести вокруг горизонтальной оси, не проходящей через его центр тяжести.

Период колебаний физического маятника

, (2)

где J – момент инерции маятника относительно оси качаний (точки подвеса); m – его масса; l – расстояние от центра тяжести до оси качаний.

Величину L = J/(ml) называют приведенной длиной физического маятника. Она равна длине такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника.

Зная T, m, и J можно по формуле (2) найти ускорение свободного падения g. Массу маятника и период его колебаний можно измерить с очень высокой точностью, но точно измерить момент инерции не удается. Указанного недостатка лишен метод оборотного маятника, который позволяет исключить момент инерции из расчетной формулы для g.

Метод оборотного маятника основан на том, что во всяком физическом маятнике можно найти такие две точки, что при последовательном подвешивании маятника за одну или другую, период колебаний его остается одним и тем же. Расстояние между этими точками представляет собой приведенную длину данного маятника.

Оборотный маятник (рис.1) состоит обычно из металлического стержня А, по которому могут передвигаться и закрепляться в том или ином положении грузы В₁ и В₂ и опорные призмы С₁ и С₂. Центр масс маятника – точка О. Период колебаний маятника можно менять, перемещая грузы или опорные призмы. Маятник подвешивают вначале на призме С₁ и измеряют период его колебаний Т₁. Затем маятник подвешивают на призме С₂ и измеряют период колебаний Т₂.

Допустим, что нам удалось найти такое положение грузов, при котором периоды колебаний маятников Т₁ и Т₂ около призм С₁ и С₂ совпадают, т.е.

.

Отсюда

(3)

По теореме Штейнера

(4)

где J₀ – момент инерции маятника относительно оси, проходящей через его центр масс и параллельной оси качаний.

С учетом формул (3) и (4) можно записать

или

.

Тогда

и

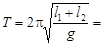
. (5)

Формула (5) аналогична формуле (1) для математического маятника. Следовательно, L = l₁ + l₂ – приведенная длина физического маятника, которая, как видно из рис.1, равна расстоянию между призмами С₁ и С₂, когда Т₁ = Т₂. Это расстояние легко может быть измерено с большой точностью.

Итак, измерение ускорения свободного падения g с помощью оборотного маятника сводится к измерению периодов Т₁ и Т₂ относительно призм С₁ и С₂, достижению их равенства (с помощью перемещения призм), измерению расстояния L = l₁ + l₂ между призмами и вычислению по формуле

. (6)

Чтобы пояснить, как достичь равенства периодов Т₁ и Т₂, исследуем, как зависит период колебаний от расстояния l между центром масс и осью качаний маятника. Согласно формулам (2) и (4), имеем

Период минимален при l_min = (рис.2). При Т > Т_min одно и то же значение Т достигается при двух разных значениях l, одно из них больше, а другое меньше l_min. Эти значения l₁ и l₂ и входят в формулу (5).

Вначале измеряется период колебаний маятника Т₁ относительно призмы С₁. Затем маятник переворачивается и измеряется период колебаний Т₂ относительно призмы С₂. Если при этом получится , то этому будет соответствовать . И для того, чтобы приблизить и Т₁, надо увеличить . Для этого надо призму С₂ передвинуть от середины стержня к краю. Если получится < Т₁, то призму С₂ надо будет передвинуть к середине стержня.

Анализ точности измерения g методом оборотного маятника показывает, что погрешность измерения слабо зависит от точности, с которой выполняется равенство Т₁ = Т₂. Достаточно добиться того, чтобы периоды оказались равны друг другу с точностью 0,5 %.

Кроме того, для получения достаточной точности измерения отношение l₁/l₂ не должно быть ни слишком малым, ни слишком большим, желательно, чтобы 1,5 < l₁ / l₂ < 3.

Экспериментальная установка представлена на рис.3. В основании 1 универсального маятника закреплена колонка 7, на которой зафиксирован верхний кронштейн 4 и нижний кронштейн 9 с фотоэлектрическим датчиком 10. Отвинчивая винт 5, верхний кронштейн можно поворачивать вокруг колонки. С одной стороны кронштейна 4 находится математический маятник 2, с другой – на вмонтированных вкладышах оборотный маятник 8.

Длину математического маятника можно регулировать винтом 3 и определять при помощи шкалы на колонке.

Оборотный маятник выполнен в виде стального стержня, на котором крепятся две призмы (ножа) С₁ и С₂ и два диска 6. Нижний кронштейн вместе с фотоэлектрическим датчиком можно перемещать вдоль колонки. Фотоэлектрический датчик соединен с универсальным электронным секундомером 11, который измеряет число колебаний n и общее время этих колебаний t. Период колебаний T = t/n.

Порядок выполнения работы

Измерения с математическим маятником проводятся в следующем порядке:

1) поместить над датчиком математический маятник, повернув соответствующим образом верхний кронштейн и установить длину математического маятника так, что бы черта на шарике была продолжением черты на корпусе фотоэлектрического датчика;

2) отклонить маятник на угол примерно 5° и придерживать шарик рукой;

3) отпустить шарик (маятник придет в движение);

4) измерить время 10 колебаний (n = 10);

5) повторить 10 раз пп.1-4;

6) по шкале на вертикальной колонке прибора определить длину маятника.

7) определить период колебаний математического маятника T = t/n, вычислить ускорение свободного падения по формуле (6) для каждого измерения и среднее значение ускорения . По результатам опыта составить таблицу:

8) рассчитать среднюю квадратическую ошибку

.

и записать окончательный результат в виде .

Измерения с оборотным маятником проводятся в следующем порядке:

1) поместить над датчиком оборотный маятник, повернув верхний кронштейн на 180°;

2) зафиксировать диски на стержне, чтобы один из них находился вблизи конца стержня, а другой вблизи его середины;

3) закрепить маятник на верхнем кронштейне на призме, находящейся вблизи конца стержня, так чтобы конец стержня пересекал оптическую ось фотоэлектрического датчика;

4) отклонить маятник примерно на 5° от положения равновесия и придерживать его рукой;

5) отпустить маятник (маятник придет в движение);

6) измерить время 10 колебаний маятника t;

7) определить период колебаний оборотного маятника T₁ = t/n;

8) снять маятник и закрепить его на второй призме;

9) измерить период Т₂, повторив пп.4-7;

10) сравнить периоды Т₂ и T₁; если Т₂ > T₁, вторую призму переместить в направлении диска, находящегося в конце стержня; если Т₂ < T₁, переместить ее в направлении середины стержня (положение дисков и первой призмы не менять);

11) снова измерить период Т₂ и сравнить его с величиной T₁; менять положение второй призмы до тех пор, пока значение периода Т₂ не станет равным значению периода T₁ с точностью до 0,5 %;

12) определить приведенную длину оборотного маятника L, измерив расстояние между призмами (по числу нарезок, которые нанесены через каждые 10 мм).

13) обработать результаты эксперимента, вычислив ускорение свободного падения по формуле (6) при Т = Т₁ = Т₂, среднюю квадратическую ошибку (здесь – погрешность измерения времени, оцениваемая исходя из точности прибора) и среднюю квадратическую ошибку

где – погрешность измерения длины, оцениваемая по цене деления измерительной линейки.

14) записать окончательный результат в виде .

Контрольные вопросы

1. Что такое математический маятник?

2. Что такое физический маятник?

3. Как с помощью маятников можно измерить ускорение свободного падения?

4. С чем связана погрешность определения g с помощью математического маятника?

5. С чем связана погрешность определения g с помощью физического маятника и как ее устранить?

6. В чем заключается метод оборотного маятника?

Работа 9. изучение прецессии гироскопа

Цель работы – экспериментально исследовать основные свойства гироскопа, изучить законы вращательного движения твердого тела.

Общие сведения

Гироскопом называют массивное симметричное тело, вращающееся с большой скоростью вокруг оси симметрии. Основное свойство гироскопа – способность сохранять неизменным направление оси вращения при отсутствии действующего на него момента внешних сил. Это свойство гироскопа основано на законе сохранения момента импульса. Гироскопы широко применяются в технике: в качестве стабилизаторов направления при движении судов, самолетов (устройство автопилот) и т.д.

Рассмотрим гироскоп, основным элементом которого является диск D, вращающийся со скоростью 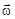вокруг горизонтальной оси ОО' (см. рисунок). Ось гироскопа шарнирно закреплена в точке C. Прибор снабжен противовесом K. Если противовес установлен так, что точка C является центром масс системы (m – масса гироскопа; m₀ – масса противовеса K; масса стержня пренебрежимо мала), то без учета трения можно записать:

т.е. результирующий момент сил, действующий на систему, равен нулю. Тогда справедлив закон сохранения момента импульса :

.

Иными словами, в этом случае const (здесь J – момент инерции гироскопа, 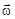– собственная угловая скорость вращения гироскопа).

Поскольку момент инерции диска относительно его оси симметрии есть величина постоянная, то вектор угловой скорости также остается постоянным как по величине, так и по направлению. Вектор 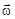направлен по оси вращения в соответствии с правилом правого винта. Таким образом, ось свободного гироскопа сохраняет свое положение в пространстве неизменным.

Если к противовесу K добавить еще один с массой m₁, то центр масс системы сместится и возникнет вращающий момент направленный перпендикулярно оси ОО' в горизонтальной плоскости. Согласно уравнению моментов, . Под действием этого вращающего момента вектор момента импульса получит приращение , совпадающее по направлению с вектором :

. (1)

Спустя время момент импульса гироскопа изменится на величину :

.

Таким образом, вектор изменяет свое направление в пространстве, все время оставаясь в горизонтальной плоскости. Учитывая, что вектор момента импульса гироскопа направлен вдоль оси вращения, поворот вектора на некоторый угол da за время dt означает поворот оси вращения на тот же угол. В результате ось симметрии гироскопа начнет вращаться вокруг неподвижной вертикальной оси ВВ' с угловой скоростью:

.

Такое движение называется регулярной прецессией, а величина – угловой скоростью прецессии.

Выясним зависимость угловой скорости прецессии гироскопа от основных параметров системы. Из формул (1) получим

При малых углах поворота из геометрических соображений (см. рисунок) , тогда , и угловая скорость прецессии

. (2)

Подвижный элемент гироскопа представляет собой массивный маховик (диск), закрепленный на оси электродвигателя. Вдоль оси маховика закреплена планка с линейной метрической шкалой. Вдоль планки может перемещаться противовес.

Угол поворота оси двигателя в горизонтальной плоскости и время движения измеряются электронной схемой с фотоэлектрическим датчиком. Кроме того, угол поворота гироскопа можно считывать по нанесенной на основании подвижной части угловой шкале. По окружности основания через каждые 5° нанесены отверстия, которые служат для считывания угла поворота при помощи фотоэлектрического датчика. На лицевой панели блока управления расположены индикаторные табло угла и времени поворота, а также кнопки «СЕТЬ», «СБРОС», «СТОП», и рукоятка регулятора скорости вращения «РЕГ. СКОРОСТИ».

Порядок выполнения работы

1. Перемещая противовес K вдоль планки, уравновесить систему (ось должна принять горизонтальное положение); измерить и записать расстояние l₀ от центра масс противовеса до оси вращения – точки С (см. рисунок).

2. Включить установку, двигатель и довести угловую скорость вращения w до 1000 мин^–1.

3. Подвесить к противовесу перегруз m₁ и дать гироскопу свободно прецессировать, записать значение m₁.

4. После поворота гироскопа на некоторый угол в пределах 30° < a < 100° записать угол a и время t поворота.

5. Повторить пп.2-4 при данной угловой скорости ротора не менее 5 раз.

6. Провести измерения для пяти-шести режимов вращения ротора, меняя угловую скорость через 1000 мин^–1 от 1000 до 6000 мин^–1. Перед каждым повторным измерением устанавливать ось гироскопа горизонтально.

7. Результаты измерений записать в таблицу:

Номер опыта

Номер измерения

w

Dw

a

Da

t

Dt

W

DW

J

DJ

…

…