
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Введение. Пример. Решить неравенство 2x2 + 4x — 6 > 0.
Пример. Решить неравенство 2x2 + 4x — 6 > 0.
1. Решаем соответствующее квадратное уравнение. Находим корни (через дискриминант).
Далее можно идти 2 способами:
I. Отмечаем корни на числовой прямой. Две точки делят прямую на три промежутка. Расставляем знаки: например, для промежутока x>1 берем х=2, подставляем в неравенство 2x2 + 4x — 6 , находим значение: 2*2^2+4*2-6=10>0, ставим знак +. Аналогично для оставшихся двух промежутков. Точки -3 и 1 выкалываем, так как неравенство СТРОГОЕ (знаки <, > - строгое неравенство). Выбираем промежуток со знаком - , записываем в ответ.
При этом, если у вас в задаче есть КОРЕНЬ или ЛОГАРИФМ, надо найти ОДЗ и не забыть пересечь получившиеся промежутки.

II. Квадратный трехчлен 2x2 + 4x — 6 имеет два действительных корня x1 = —3, x2 =1. Поэтому парабола у = 2x2 + 4x — 6 пересекает ось х в двух точках, абсциссы которых равны —3 и 1. Поскольку коэффициент при x2 больше нуля, парабола у = 2x2 + 4x — 6 направлена вверх (рис. 89).
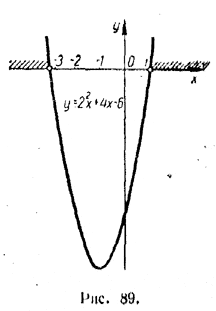
Из рисунка видно, что трехчлен 2x2 + 4x — 6 положителен при х < — 3 и при х >1
Введение
На сегодняшний день строительные рынки России и других стран СНГ изобилуют новейшими строительными материалами различных характеристик и областей применения. Совершенно ясно и очевидно, что разобраться в таком многообразии товаров и услуг практически нереально. Однако, как нам кажется, современный инженер-строитель, да и просто любой уважающий себя частный застройщик просто обязан знать и уметь правильно использовать те или иные характеристики большинства современных строительных материалов.
Мы же в своей работе остановились на, как нам кажется, одном из самых популярных среди застройщиков и самых любимых среди заказчиков, но в то же время неизученном классе отделочных материалов. Итак, речь пойдет об искусственных декоративных отделочных камнях.
Как известно, понятие «искусственный камень» чрезвычайно широко: сюда входят и кирпичи, и бетоны, и полимерфосфогипс. Но в современном строительстве в роли отделочного материала применяют, в основном, камни на основе полиэфирных смол и наполнителя из крошки природного камня, а также камни, которые представляют собой цветные бетоны, с фактурой натурального камня. У обоих видов камней удивительные свойства, при грамотном их использовании можно получить стену, по внешнему виду ничуть не отличающуюся от стены из натурально камня, но по гораздо меньшей себестоимости. Кроме того, искусственный камни на основе полиэфирных смол позволяют получать поверхностные части мебели, а также различные декоративные изделия.
Мы в своей работе постарались осветить более подробно такие аспекты, как: определение и классификация искусственных камней, история распространения отделочных искусственных камней, их изготовление и применение, наиболее характерные свойства искусственных камней. Также более подробно рассмотрены такие виды, как: искусственны мрамор, жидкий камень, агломерированный камень, камень Solid Surface.
Мы считаем, что эта работа представляет практический интерес для всех тех, кто желает более подробно разобраться в мире искусственных каменных отделочных материалов.
Дата добавления: 2015-01-10; просмотров: 246; Мы поможем в написании вашей работы!; Нарушение авторских прав |