Какой режим работы пассивной цепи, содержащей катушки индуктивности и конденсаторы, называют резонансом? Какие два основных вида резонанса известны?

Ответ: Резонансом называют режим, когда в цепи, содержащей индуктивности и емкости, ток совпадает по фазе с напряжением. Входные реактивные сопротивление и проводимость равны нулю: x=ImZ=0 и B=ImY=0. Цепь носит чисто активный характер: Z=R; сдвиг фаз отсутствует ( = 0). В цепи, содержащей последовательно соединенные участки с индуктивным и емкостным характерами сопротивлений, резонанс называется резонансом напряжений. Рассмотрим простейшую цепь такого вида (рис. 2.23), которую часто называют последовательным контуром. Для нее резонанс наступает при x=x_L–x_C=0 или x_L=x_C, откуда: 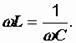(2.33)

Напряжения на индуктивности и емкости в этом режиме равны по величине и, находясь в противофазе, компенсируют друг друга. Все приложенное к цепи напряжение приходится на ее активное сопротивление (рис. 2.42, а).

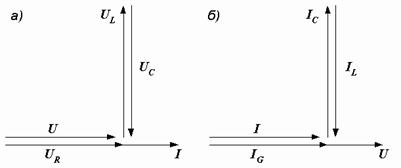
Рис. 2.42. Векторные диаграммы при резонансе напряжений (а) и токов (б)

Напряжения на индуктивности и емкости могут значительно превышать напряжения на входе цепи. Их отношение, называемое добротностью контура Q, определяется величинами индуктивного (или емкостного) и активного сопротивлений: . Добротность показывает, во сколько раз напряжения на индуктивности и емкости при резонансе превышают напряжение, приложенное к цепи. В радиотехнических цепях она может достигать нескольких сотен единиц. Из условия (2.33) следует, что резонанса можно достичь, изменяя любой из параметров – частоту, индуктивность, емкость. При этом меняются реактивное и полное сопротивления цепи, а вследствие этого – ток, напряжение на элементах и сдвиг фаз. Не приводя анализа формул, показываем графические зависимости некоторых из этих величин от емкости (рис. 2.43). Емкость 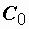, при которой наступает резонанс, можно определить из формулы (2.33): 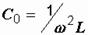. Если, например, индуктивность контура L =0,2 Гн, то при частоте 50 Гц, резонанс наступит при емкости: мкФ.

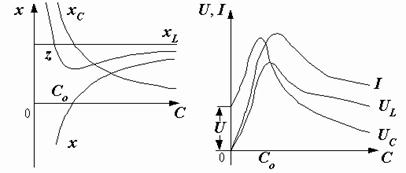
Рис. 2.43. Зависимости параметров режима от емкости

Аналогичные рассуждения можно провести и для цепи, состоящей из параллельно соединенных R, L и C (рис. 2.31, а). Векторная диаграмма ее резонансного режима приведена на рис. 2.42, б. Рассмотрим теперь более сложную цепь с двумя параллельными ветвями, содержащими активные и реактивные сопротивления (рис. 2.44, а).

Рис. 2.44. Разветвленная цепь (а) и ее эквивалентная схема (б)

Для нее условием резонанса является равенство нулю ее реактивной проводимости:ImY=0. Это равенство означает, что мы должны мнимую часть комплексного выражения Y приравнять к нулю. Определяем комплексную проводимость цепи. Она равна сумме комплексных проводимостей ветвей:

.

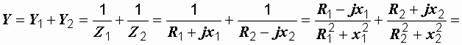
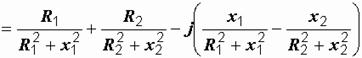Приравнивая к нулю выражение, стоящее в круглых скобках, получаем:

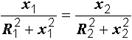или 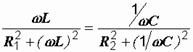. (2.34)

Левая и правая части последнего выражения представляют собой не что иное, как реактивные проводимости первой и второй ветвей B₁ и B₂. Заменяя схему на рис. 2.44, а эквивалентной (рис. 2.44, б), параметры которой вычисляем по формуле (2.31), и используя условие резонанса(B=B₁–B₂=0), снова приходим к выражению (2.34). Схеме на рис. 2.44, б соответствует векторная диаграмма, приведенная на рис. 2.45:

Рис. 2.45. Векторная диаграмма резонансного режима разветвленной цепи

Резонанс в разветвленной цепи называется резонансом токов. Реактивные составляющие токов параллельных ветвей противоположны по фазе, равны по величине и компенсируют друг друга, а сумма активных составляющих токов ветвей дает общий ток.