Комплексное сопротивление участка цепи . Чему равна комплексная проводимость этого участка?

Ответ: Расчет цепей переменного синусоидального тока может производиться не только путем построения векторных диаграмм, но и аналитически – путем операций с комплексами, символически изображающими синусоидальные ЭДС, напряжения и токи. Достоинством векторных диаграмм является их наглядность, недостатком – малая точность графических построений. Применение символического метода позволяет производить расчеты цепей с большой степенью точности. Символический метод расчета цепей синусоидального тока основан на законах Кирхгофа и законе Ома в комплексной форме. Уравнения, выражающие законы Кирхгофа в комплексной форме, имеют совершенно такой же вид, как и соответствующие уравнения для цепей постоянного тока. Только токи, ЭДС, напряжения и сопротивления входят в уравнение в виде комплексных величин. 1. Первый закон Кирхгофа в комплексной форме:

.

(3)

2. Второй закон Кирхгофа в комплексной форме:

(4)

или применительно к схемам замещения с источниками ЭДС

.

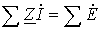(5)

3. Соответственно матричная запись законов Кирхгофа в комплексной форме имеет вид:

 первый закон Кирхгофа:

. ;

(6)

 второй закон Кирхгофа

.

(7)

Пример. Дано:

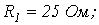
Определить:	1) полное комплексное сопротивление цепи ;
2) токи
Рис. 2

Решение: 1. 2. .

3.

.

4. Принимая начальную фазу напряжения за нуль, запишем: .

Тогда: . 5. Поскольку ток распределяется обратно пропорционально сопротивлению ветвей (это вытекает из закона Ома), то:

6. . 7. Аналогичный результат можно получить, составив для данной схемы уравнения по законам Кирхгофа в комплексной форме:

или после подстановки численных значений параметров схемы