Привести закон Ома в комплексной форме записи.

Ответ: Рассмотрим элементарную цепь (рис. 2.63).

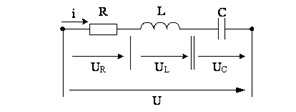
Рисунок 2.63

. (2.85). Выразим каждую из величин входящих в (2.85), в виде комплекса и подставим их в уравнение (2.85):

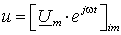; ; , — согласно теореме дифференцирования. Согласно теореме интегрирования: ; . (2.86). Если в любой момент времени равны мнимые части каких-либо комплексных функций, то равны и сами функции. Знак мнимой части im можно опустить. Величина e^jwt ? 0 ни при каком значении t. На нее можно сократить. В результате получим: , (2.87)

где: (2.88) — комплекс полного сопротивления цепи. Таким образом, (2.89). Это и есть закон Ома для комплексных амплитуд. Разделив обе части на , получим закон Ома для действующих значений: 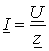. (2.90). Комплексы полного сопротивления и полной проводимости: Оба комплекса употребляются как в алгебраической, так и в показательной формах: Комплекс полного сопротивления:

, где: — модуль комплекса полного сопротивления; или просто модуль сопротивления; — угол сдвига фаз между током и напряжением на данном участке. Наоборот: .

Комплекс полной проводимости: , (2.91)

иначе: .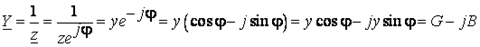

Обратный переход: .