Построить векторную диаграмму тока и напряжений участка цепи с реальной индуктивной катушкой? Как называют эту диаграмму?

Ответ: Реальная катушка индуктивности обычно имеет и активное сопротивление, которым нельзя пренебречь. На рисунке 1 “а” показана цепь катушки индуктивность которой L, а активное сопротивление R. на рисунке 1 “б” изображены кривые мгновенных значений напряжения u и тока i в цепи R и L, а на рисунке 1 “в” - взаимное расположение векторов напряжения Um и тока Im, сдвинутых относительно один другого на угол . Если в цепи с R и L проходит синусоидальный ток , то мгновенное значение активной составляющей напряжения может быть определено как . Мгновенное значение напряжения на индуктивном сопротивлении в соответствии с формулой: . (1).

Мгновенное же значение напряжения, приложенного ко всей цепи, равно алгебраической сумме мгновенных значений напряжений на активном и индуктивном сопротивлениях:

(2) Так как оба слагаемых этой суммы – синусоидальные величины, изменяющиеся с одинаковой частотой ω, то результирующее напряжение uтоже синусоидально и имеет ту же частоту. Это результирующее напряжениеu представлено на рисунке 1 “б”. Векторная диаграмма амплитудных значений напряжения и тока приведена на рисунке “в”. Анализ схем с несколькими сопротивлениями в цепи удобно проводить на векторных диаграммах действующих значений величин, которые могут быть измерены приборами, например вольтметром и амперметром (рисунок 1 “а”). Для перехода к диаграмме амплитудных величин каждый вектор действующего значения следует увеличивать в раз, так как , а . Порядок построения векторной диаграммы для схемы 1 “а” таков. Общим для обоих сопротивлений R и X_L в этой схеме является ток, действующее значение которого измеряют амперметром А. Откладываем этот ток в определенном, удобном для нас, масштабе (рисунок 1 “а”) по горизонтали, так как начальная фаза тока i=I_msin ω t равна нулю (рисунок 1 “б”). Напряжение U_a совпадает по фазе с током, поскольку оно приложено у участку цепи, имеющему только активное сопротивление R. Поэтому вектор совпадает по фазе с током, поскольку оно приложено к участку цепи, имеющему только активное сопротивление R. Поэтому откладываем вдоль вектора .Масштаб напряжения также выбираем удобным для построения . Например если для тока мы приняли масштаб 1:1, то есть 1 ампер отложим в 1 см длины вектора , то для напряжения удобнее принять масштаб 100:1, то есть 100 вольт отложить в 1 см. Напряжение 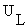опережает ток I по фазе на угол , так как оно приложено к участку цепи, имеющему только индуктивное сопротивление. Поэтому вектор отложим в направлении, перпендикулярном вектору . Причем масштаб вектора должен быть равен масштабу . Складывая затем геометрический и , получим вектор действующего значения общего напряжения , приложенного к цепи с R и X_L. На векторной диаграмме (рисунок 2 “а”) векторы , и образуют прямоугольный треугольник называют треугольником напряжений. По теореме Пифагора для этого треугольника: (4). Если все стороны треугольника напряжения разделить на величину Iто получиться так называемый треугольник сопротивлений (рисунок 2 “б”). Из этого треугольника: (5) (Z-полное сопротивление всей цепи, Ом). Если известно напряжение U, приложенное к к исследуемой цепи (оно может быть измерено вольтметром Vна рисунке 1 “а”), а также ток в цепи I (он измеряется амперметром А), то полное сопротивление всей цепи: , отсюда: (5). Формула 5 является математическим выражением закона Ома для индуктивной и активной нагрузкой, с последовательным соединением индуктивного и резисторного элементов. Пользуясь векторными диаграммами, можно написать следующие соотношения между составляющими напряжения и найти значение угла . Так, из рисунка 2 “а”

(6). Из треугольника сопротивлений: 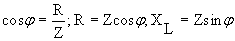(7). В цепи с параллельным включением активного и индуктивного сопротивления аналогично уравнению 6: (8)