Полагая, что сопротивление R и индуктивность L катушки индуктивности известны, определить параметры эквивалентной параллельной схемы замещения.

Ответ: Параллельное соединение активного сопротивления,
индуктивности и емкости: Рассмотрим схему, состоящую из параллельно соединенных активного и реактивных элементов (рис. 2.31, а). Требуется по известным G, В_L, В_C, U рассчитать токи. Как и прежде, задачу будем решать двумя методами. 1. М е т о д в е к т о р н ы х д и а г р а м м:

Токи ветвей находятся сразу: , , 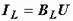. Для определения общего тока необходимо построить векторную диаграмму (рис. 2.31, б). Построение начинаем с вектора напряжения, так как оно является общим для всех ветвей. Из векторной диаграммы имеем: или , где – полная проводимость цепи, равная: . Разность индуктивной и емкостной проводимостей представляет собой общую реактивную проводимость цепи .

Рис. 2.31. Электрическая цепь и ее векторная диаграмма

Векторы токов на диаграмме образуют треугольник токов. Его горизонтальный катет, представляющий проекцию вектора тока на вектор напряжения, называется активной составляющей тока и равен току в активном элементе цепи: (рис. 2.32, а). Проекция вектора тока на направление, перпендикулярное напряжению, – это реактивная составляющая тока. Она равна суммарному току реактивных элементов и определяется как разность длин векторов:

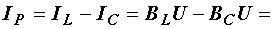
(см. рис. 2.31, б и 2.32, а).

Рис. 2.32. Треугольники токов и проводимостей

Разделив все стороны треугольника токов на 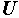, получим треугольник проводимостей (рис. 2.32, б), стороны которого связаны следующими соотношениями: , , , .

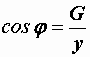2. С и м в о л и ч е с к и й м е т о д. Раньше были получены следующие формулы: , , . Подставляя их в уравнение первого закона Кирхгофа, получаем: или , где – комплексная проводимость цепи, равная:

Дата добавления: 2015-01-14; просмотров: 11; Нарушение авторских прав