
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
В чём сущность и достоинство символического метода расчёта цепей синусоидального тока?
Ответ: Метод основан на символическом изображении действительных синусоидальных функций времени комплексными числами.
Комплексное число С характеризуется следующими параметрами:
 с – модуль комплексного числа
с – модуль комплексного числа  ,
,  ;
;
a – аргумент комплексного числа,  .
.
 – алгебраическая форма записи;
– алгебраическая форма записи;
 – тригонометрическая форма записи;
– тригонометрическая форма записи;
 – форма Эйлера (показательная форма);
– форма Эйлера (показательная форма);
 – мнимая единица.
– мнимая единица.
Арифметические операции над комплексными числами:
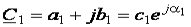 ,
,  ;
;

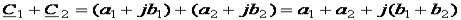 ;
;


Изображение синусоидальных токов, напряжений и ЭДС комплексными числами. Пусть комплексное число  . Вектор вращается, т.е.
. Вектор вращается, т.е. 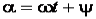 ;
; 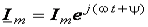 ,
, 
Для  имеем
имеем  . Для того чтобы перейти от комплексного числа к мгновенному значению, нужно выразить это комплексное число в тригонометрической форме с учетом вращения вектора и взять коэффициент при мнимой части. Для перехода от мгновенного значения к комплексу в качестве модуля берется амплитуда, а в качестве аргумента – начальная фаза.
. Для того чтобы перейти от комплексного числа к мгновенному значению, нужно выразить это комплексное число в тригонометрической форме с учетом вращения вектора и взять коэффициент при мнимой части. Для перехода от мгновенного значения к комплексу в качестве модуля берется амплитуда, а в качестве аргумента – начальная фаза.
Комплекс действующего значения 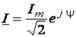 , а сопряженный комплекс тока
, а сопряженный комплекс тока 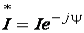 .
.
Изображение сопротивлений и мощностей в комплексной форме (таблица). Есть  и
и  , причем
, причем  . Тогда векторная диаграмма имеет вид рис. 1.23.
. Тогда векторная диаграмма имеет вид рис. 1.23.


Найдём 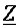 из закона Ома
из закона Ома 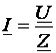 :
: 
Комплекс полной мощности: 
Для других видов цепи 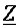 и
и  приведены в таблице. Алгоритм расчета цепи символическим методом:
приведены в таблице. Алгоритм расчета цепи символическим методом:
· Переходим от мгновенных или действующих значений I и U к комплексным.
· Изображаем сопротивления в комплексной форме.
· Используя любой из известных методов расчета цепей постоянного тока, рассчитываем цепь, оперируя комплексными числами.
· После окончания расчетов для контроля строим векторную диаграмму.
· Переходим от найденных комплексов к мгновенным или действующим значениям.
Дата добавления: 2015-01-14; просмотров: 432; Мы поможем в написании вашей работы!; Нарушение авторских прав |