Если в результате столкновения двух тел сохраняется кинетическая энергия, такой удар называется абсолютно упругим.

Примером абсолютно упругих ударов могут быть столкновения бильярдных шаров. Мы рассмотрим простейший случай такого столкновения – центральное столкновение.

Центральным называется столкновение, при котором скорость одного шара проходит через центр масс другого шара. (Рис. 2.)

Пускай один шар покоится, а второй налетает на него с какой-то скоростью , которая, согласно нашему определению, проходит через центр второго шара. Если столкновение центральное и упругое, то при столкновении возникают силы упругости, действующие вдоль линии столкновения. Это приводит к изменению горизонтальной составляющей импульса первого шара, и к возникновению горизонтальной составляющей импульса второго шара. После удара второй шар получит импульс, направленный направо, а первый шар может двигаться как направо, так и налево – это будет зависеть от соотношения между массами шаров. В общем случае, рассмотрим ситуацию, когда массы шаров различны.

Закон сохранения импульса выполняется при любом столкновении шаров:

В случае абсолютно упругого удара, также выполняется закон сохранения энергии:

Получаем систему из двух уравнений с двумя неизвестными величинами. Решив ее, мы получим ответ.

Скорость первого шара после удара равна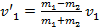

заметим, что эта скорость может быть как положительной, так и отрицательной, в зависимости от того, масса какого из шаров больше. Кроме того, можно выделить случай, когда шары одинаковые. В этом случае после удара первый шар остановится. Скорость второго шара, как мы ранее отметили, получилась положительной при любом соотношении масс шаров:

Наконец, рассмотрим случай нецентрального удара в упрощенном виде – когда массы шаров равны. Тогда, из закона сохранения импульса мы можем записать: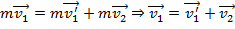

А из того, что кинетическая энергия сохраняется:

Нецентральным будет удар, при котором скорость налетающего шара не будет проходить через центр неподвижного шара (рис. 3). Из закона сохранения импульса, видно, что скорости шаров составят параллелограмм. А из того, что сохраняется кинетическая энергия, видно, что это будет не параллелограмм, а квадрат.

Таким образом, при абсолютно упругом нецентральном ударе, когда массы шаров равны, они всегда разлетаются под прямым углом друг к другу.

21. Абсолютно твердое тело - физическая модель. Поступательное и вращательное движение твердого тела. Угловая скорость и угловое ускорение.
Связь угловых и линейных величин.

Вращательное движение - движение, при котором все точки тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения.Ось вращения проходит через центр тела, через тело, а может находится вне его.Вращательное движение материальной точки - движение материальной точки по окружности.Основные характеристики кинематики вращательного движения: угловая скорость, угловое ускорение.Угловое перемещение - векторная величина, характеризующая изменение угловой координаты в процессе ее движения.

Угловая скорость - отношение угла поворота радиус-вектора точки к промежутку времени, за который произошел этот поворот.(направление вдоль оси вокруг которой вращается тело)

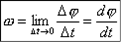
Частота вращения - физическая величина, измеряемая числом полных оборотов, совершаемых точкой в единицу времени при равномерном движении в одном направлении(n)

Период вращения - промежуток времени, в течение которого точка совершает полный оборот,

двигаясь по окружности (T) N – число оборотов, совершаемых телом за время t.

Угловое ускорение - величина харатеризующая изменение вектора угловой скорости со временем.

Связь между угловыми и линейными величинами:

связь между линейной и угловой скоростью.

связь между тангенциальным и угловым ускорением.

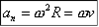вязь между нормальным (центростремительным) ускорением, угловой скоростью и линейной скоростью.

22. Момент инерции точки относительно вращения - мера инертности во
вращательном движении.

Момент силы - величина, характеризующая вращательный эффект силы при действии её на твёрдое тело. Различают Момент силы относительно центра (точки) и относительно оси.

1.Момент силы относительно центра О величина векторная. Его модуль Mo = Fh, где F - модуль силы, a h - плечо (длина перпендикуляра, опущенного из О на линию действия силы)

С помощью векторного произведения момент силы выражается равенством Mo = [rF], где r - радиус-вектор, проведённый из О в точку приложения силы.

2.Момент силы относительно оси величина алгебраическая, равная проекции на эту ось.

Момент силы (крутящий момент; вращательный момент; вращающий момент) — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы.

это выражение является вторым законом Ньютона для вращательного движения.

Оно справедливо только тогда:

а) если под моментом М понимают часть момента внешней силы, под действием которой происходит вращение тела вокруг оси - это тангенциальная составляющая.

б) нормальная составляющая из момента силы не участвует во вращательном движении, так как Mn старается сместить точку с траектории, и по определению тождественно равна 0, при r- const Mn=0, а Mz - определяет силу давления на подшипники.

Момент инерции - скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении.

Момент инерции зависит от массы тела и от расположения частиц тела относительно оси вращения.

Тонкий обруч Стрежень (закреп. по середине) Стержень См.

Однородный цилиндр Диск Шар.

(справа картинка к пункту 2 в т. Штейнера)

Теорема Штейнера.

Момент инерции данного тела относительно, какой либо данной оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси.

Согласно теореме Гюйгенса - Штейнера - момент инерции тела J относительно произвольной оси равен сумме:

1)момента инерции этого тела Jо, относительно оси, проходящий через центр масс этого тела, и параллельной рассматриваемой оси,

2) произведения массы тела на квадрат расстояния между осями.