
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение момента инерции однородного стержня относительно оси,проходящей через центр масс.
В общем случае моменты инерции различных тел можно найти по формуле I=mmR2,
где m - коэффициент пропорциональности, который зависит от формы тела и его расположения относительно оси вращения.
Найдем момент инерции однородного стержня относительно оси, проходящей через один из его концов, перпендикулярно продольной геометрической оси симметрии (рис. 5.2).

Пусть ось вращения ВВ проходит через правый конец стержня (точка Г), тогда
I=mmL2, где L - длина стержня.
Согласно теореме Штейнера имеем 
Величину момента инерции Ic относительно оси, проходящей через центр масс (точка С), представим как сумму моментов инерции двух стержней с длинами ДС=СГ=L/2 и массой каждого, равной m/2 стержня, т.е. 
Подставим значения момента инерции I и Ic в формулу теоремы Штейнера и найдем m: 
После преобразования получим, что m = 1/3.
Следовательно, момент инерции стержня относительно оси, проходящей через центр масс, 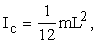
а относительно оси ВВ, 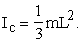
Дата добавления: 2015-01-15; просмотров: 331; Мы поможем в написании вашей работы!; Нарушение авторских прав |