Работа и кинетическая энергия вращательного движения.

Кинетическая энергия и работа при вращении тела. Рассмотрим абсолютно твердое тело, вращающееся вокруг неподвижной оси. Если мысленно разбить это тело на n точек массами m₁, m₂, …, m_n, находящихся на расстояниях r₁, r₂, …, r_n от оси вращения, то при вращении они будут описывать окружности и двигаться с различными линейными скоростями v₁, v₂, …, v_n. Так как тело абсолютно твердое, то угловая скорость вращения точек будет одинакова:

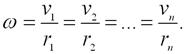
Кинетическая энергия вращающегося тела есть сумма кинетических энергий его точек, т.е.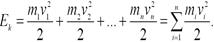
Учитывая связь между угловой и линейной скоростями, получим:

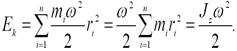
Сопоставление формулы (4.9) с выражением для кинетической энергии тела, движущегося поступательно со скоростью v, показывает, что момент инерции является мерой инертности тела во вращательном движении.
Если твердое тело движется поступательно со скоростью v и одновременно вращается с угловой скоростью ω вокруг оси, проходящей через его центр инерции, то его кинетическая энергия определяется как сумма двух составляющих:

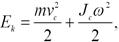
где v_c – скорость центра масс тела; J_c - момент инерции тела относительно оси, проходящей через его центр масс.
Моментом силы относительно неподвижной оси zназывается скалярная величина M_z, равная проекции на эту ось вектора M момента силы, определенного относительно произвольной точки 0 данной оси. Значение момента M_z не зависит от выбора положения точки 0 на оси z.
Если ось z совпадает с направлением вектора M, то момент силы представляется в виде вектора, совпадающего с осью: M_z = [rF]_zНайдем выражение для работы при вращении тела. Пусть сила F приложена к точке В, находящейся от оси вращения на расстоянии r (рис. 4.6); α – угол между направлением силы и радиусом-вектором r. Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела.
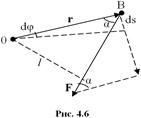При повороте тела на бесконечно малый угол dφ точка приложения В проходит путь ds = rdφ, и работа равна произведению проекции силы на направление смещения на величину смещения: dA = Fsinα*rdφ

Учитывая, что Frsinα = M_z можно записать dA = M_zdφ, где M_z - момент силы относительно оси вращения. Таким образом, работа при вращении тела равна произведению момента действующей силы на угол поворота.
Работа при вращении тела идет на увеличение его кинетической энергии: dA = dE_k

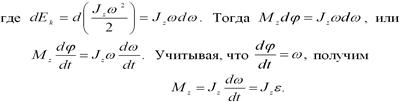
Уравнение представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.