Идеальный газ - физическая модель. Уравнение Клапейрона-Менделеева. Изопроцессы. Закон Дальтона.

Идеальный газ — математическая модель газа, в которой в рамках молекулярно-кинетической теории предполагается, что: 1) потенциальной энергией взаимодействия частиц, составляющих газ, можно пренебречь по сравнению с их кинетической энергией; 2) суммарный объём частиц газа пренебрежимо мал; 3) между частицами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги; 4) время взаимодействия между частицами пренебрежимо мало по сравнению со средним временем между столкновениями.В рамках термодинамики идеальным называется газ, подчиняющийся термическому уравнению состояния Клапейрона — Менделеева

Модель широко применяется для решения задач термодинамики газов и задач аэрогазодинамики.Свойства идеального газа на основе молекулярно-кинетических представлений определяются исходя из физической модели идеального газа, в которой приняты следующие допущения:

• Диаметр молекулы 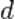пренебрежимо мал по сравнению со средним расстоянием между ними ( ) .

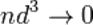• Импульс передается только при соударениях, то есть силы притяжения между молекулами не учитываются, а силы отталкивания возникают только при соударениях.

• Суммарная энергия частиц газа постоянна, если отсутствует теплопередача и газ не совершает работы.

Основное уравнение молекулярно-кинетической теории идеального газа утверждает:

Произведение давления идеального газа на его объем пропорционально плотности числа молекул в газе и средней кинетической энергии поступательного движения отдельной молекулы, т.е.

Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

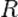,• — давление, • — молярный объём, • — универсальная газовая постоянная

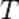— абсолютная температура, К.

Изопроцессы — термодинамические процессы, во время которых количество вещества и ещё одна из физических величин — параметров состояния: давление, объём или температура — остаются неизменными. Так, неизменному давлению соответствует изобарный процесс, объёму — изохорный, температуре — изотермический, энтропии — изоэнтропийный (например, обратимый адиабатический процесс). Линии, изображающие данные процессы на какой-либо термодинамической диаграмме, называются изобара, изохора, изотерма и адиабата соответственно. Изопроцессы являются частными случаями политропного процесса.

Изобарный процесс (др.-греч. ισος, isos — «одинаковый» + βαρος, baros — «вес») — процесс изменения состояния термодинамической системы при постоянном давлении ( )

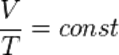
Изохорный процесс (от греч. хора — занимаемое место) — процесс изменения состояния термодинамической системы при постоянном объёме ( ). Для идеальных газов изохорический процесс описывается законом Шарля: для данной массы газа при постоянном объёме, давление прямо пропорционально температуре:

Изотермический процесс (от греч. «термос» — тёплый, горячий) — процесс изменения состояния термодинамической системы при постоянной температуре ( )( ).

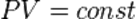Изоэнтропийный процесс — процесс изменения состояния термодинамической системы при постоянной энтропии ( 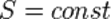). Изоэнтропийным является, например, обратимый адиабатический процесс: в таком процессе не происходит теплообмена с окружающей средой. Идеальный газ в таком процессе описывается следующим уравнением:

где — показатель адиабаты, определяемый типом газа.

Законы Дальтона — два физических закона, определяющих суммарное давление и растворимость смеси газов. Сформулированы Джоном Дальтоном в начале XIX века