Момент импульса. Закон сохранения момента импульса механической системы.

Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:

где r - радиус-вектор, проведенный из точки О в точку A, p=mv - импульс материальной точки; L - псевдовектор, направление которого совпадает с направлением поступательного движения правого винта при его вращении от r к р.

Модуль вектора момента импульса
где α - угол между векторами r и р, l - плечо вектора р относительно точки О.
Моментом импульса относительно неподвижной оси z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса L_z не зависит от положения точки О на оси z.
При вращении абсолютно твердого тела вокруг неподвижной оси z каждая точка тела движется по окружности постоянного радиуса r_i со скоростью v_i . Скорость v_i и импульс m_iv_i перпендикулярны этому радиусу, т. е. радиус является плечом вектора m_iv_i . Значит, мы можем записать, что момент импульса отдельной частицы равен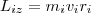
и направлен по оси в сторону, определяемую правилом правого винта.
Монет импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:

Используя формулу v_i = ωr_i, получим т. е. 2)

Таким образом, момент импульса твердого тела относительно оси равен моменту инерции тела относительно той же оси, умноженному на угловую скорость. Продифференцируем уравнение (2) по времени:

т. е.
Эта формула - еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.
Можно показать, что имеет место векторное равенство
В замкнутой системе момент внешних сил и откуда
Выражение представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.
Закон сохранения момента импульса также как и закон сохранения энергии является фундаментальным законом природы. Он связан со свойством симметрии пространства - его изотропностью, т. е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол).
Здесь мы продемонстрируем закон сохранения момента импульса с помощью скамьи Жуковского. Человек, сидящий на скамье, вращающаяся вокруг вертикальной оси, и держащий в вытянутых руках гантели, вращается внешним механизмом с угловой скоростью ω₁. Если человек прижмет гантели к телу, то момент инерции системы уменьшится. Но момент внешних сил равен нулю, момент импульса системы сохраняется и угловая скорость вращения ω₂ увеличивается. Аналогичным образом, гимнаст во время прыжка через голову поджимает к туловищу руки и ноги, с целью уменьшить свой момент инерции и тем самым увеличить угловую скорость вращения.
28. Стационарное течение вязкой жидкости.

Идеальная жидкость является физической моделью, позволяющей понять суть явления в некотором приближении. Всем реальным жидкостям присущи вязкость или внутреннее трение, что приводит к появлению у них принципиально новых свойств. В частности, возникшее в жидкости движение после прекращения действия причин, его вызвавших, постепенно замедляется. Следовательно, жидкость при своем движении в трубе испытывает сопротивление. Такого рода сопротивление называют вязким, подчеркивая тем самым отличие от сопротивления в твердых телах.

В твердых телах в случае попытки изменения их формы (например, при сдвиге одной части тела относительно другой) возникает сила упругой деформации сдвига, пропорциональная смещению атомов, находящихся в узлах кристаллической решетки соседних атомных слоев. В жидкости эта сила пропорциональна величине изменения скорости, наблюдающейся при переходе между соседними слоями взаимодействующих молекул.

Еще Ньютон установил опытным путем, что при скольжении друг относительно друга двух параллельных плоскостей, пространство между которыми заполнено жидкостью, силы вязкого трения препятствуют этому скольжению. Так, при движении со скоростью v верхней плоскости с площадью Sотносительно нижней, возникает сила вязкого трения, направленная против движения и равная F_т = μS ^v/_h.

Эта сила пропорциональна площади S и изменению скорости на единицу длины в поперечном направлении ^v/_h (градиенту скорости в направлении перпендикулярном движению) и зависит также от вязкости жидкости μ.

Вышепривёдённая формула справедлива, если расстояние h между пластинами значительно меньше их линейных размеров . Важно отметить, что частицы жидкости, прилегающие к верхней пластине, движутся вместе с нею со скоростью v (увлекаются пластиной). Напротив, частицы жидкости вблизи нижней (неподвижной) пластины находятся в покое (прилипают к пластине). Если мысленно разбить жидкость на параллельные плоские слои, движущиеся равномерно, то нетрудно понять, что каждый вышележащий слой увлекает за собой нижний соседний слой с силой F_т. В свою очередь, этот нижний слой тормозит движение верхнего слоя с силой, численно равной F_т. На каждый слой действует сверху и снизу две равные, но противоположные силы. Скорость слоев нарастает линейно с их высотой (см. рисунок ниже), а сила трения передается от одному слоя к другому. Как результат, усилие F = F_т, приложенной к верхней пластине, передается на нижнюю пластину. Коэффициент вязкости среды определяется экспериментально, например, по скорости ее истечения через трубку известных размеров. Как показывает опыт с нагреванием, вязкость жидкости уменьшается, а газов - увеличивается.

Для анализа течения вязкой жидкости в гидро динамике используется уравнение Навье-Стокса:

где — оператор Гамильтона, Δ — оператор Лапласа, — вектор скорости, t — время, ν — коэффициент кинематической вязкости, ρ — плотность,P — давление, — вектор плотности массовых сил. Уравнение Навье-Стокса является основным при расчете движения вязкой несжимаемой жидкости. Однако в общем случае оно не решается методами современной математики, и на практике приходится ограничиваться решением лишь частных задач. Одной из таких задач является течение невязкой несжимаемой жидкости, подчиняющееся уравнению Бернулли. Ранее мы получили условие, при котором сжимаемостью жидкости или газа можно пренебречь. Теперь мы выясним, в каких случаях можно пренебречь действием сил вязкости.

Течение вязкой жидкости по трубам в зависимости от ряда условий может быть ламинарным (или слоистым) и турбулентным (или вихревым). В случае ламинарного течения все молекулы жидкости движутся параллельно оси трубы и, находясь на одинаковом расстоянии от осевого центра трубы, имеют равные скорости

Для турбулентного движения характерно наличие нормальной (перпендикулярной направлению течения жидкости) составляющей скорости движения молекул и резкий спад скорости течения при приближении к границам. Траектория движения молекул представляет собой сложную кривую линию.

Характер течения можно установить, пользуясь безразмерной величиной - числом Рейнольдса:

Re = ρ·v_ср·r/μ, где ρ - плотность жидкости; v_ср - средняя (по сечению трубы) скорость потока; μ - коэффициент вязкости жидкости; r - характерный геометрический размер, в частности, радиус сечения цилиндрической трубы

Число Рейнольдса характеризующет отношение сил инерции и сил вязкости. Таким образом, текущую жидкость можно рассматривать как невязкую, если число Рейнольдса для такого течения Re>1.

Статистический и термодинамический методы изучения строения вещества. Термодинамическая система. Термодинамические параметры. Молярная масса. Число Авогадро. Равновесные состояния и квазиравновесные процессы.

Молекулярная физика и термодинамика — разделы физики, в которых изучаются зависимости свойств тел от их строения, взаимодействия между частицами, из которых состоят тела, и характера движения частиц. Для исследования физических свойств макроскопических систем, связанных с огромным числом содержащихся в них атомов и молекул, применяют двакачественно различных и взаимно дополняющих друг друга метода: статистический (или молекулярно-кинетический) и термодинамический.

Статистический метод— это метод исследования систем из большого числа частиц, оперирующий статистическими закономерностями и средними (усредненными) значениями физических величин, характеризующих всю систему. Этот метод лежит в основе молекулярной физики — раздела физики, изучающего строение и свойства вещества исходя из молекулярно- кинетических представлений, основывающихся на том, что все тела состоят из атомов, молекул или ионов находящихся в непрерывном хаотическом движении. В дальнейшем мы будем использовать термин "молекула" имея ввиду мельчайшую структурную единицу (элемент) данного вещества.

Термодинамический метод— это метод исследования систем из большого числа частиц, оперирующий величинами, характеризующими систему в целом(например, давление, объем, температура) при различных превращениях энергии, происходящих в системе, не учитывая при этом внутреннего строения изучаемых тел и характера движения отдельных частиц. Этот метод лежит в основе термодинамики — раздела физики, изучающего общие свойства макроскопических систем, находящихся в состоянии термодинамического равновесия, и процессы перехода между этими состояниями. Термодинамическая система.Термодинамика имеет дело с термодинамической системой — совокупностью макроскопических тел, которые взаимодействуют и обмениваются энергией как между собой, так и с другими телами (внешней средой). Термодинамические системы, не обменивающиеся с внешней средой ни энергией, ни веществом, называются замкнутыми. Основа термодинамического метода — определение состояния термодинамической системы. Состояние системы задается термодинамическими параметрами (параметрами состояния)— совокупностью физических величин, характеризующих свойства термодинамической системы. Обычно в качестве параметров состояния выбирают температуру, давление и объем. Параметры состояния системы могут изменяться. Любое изменение в термодинамической системе, связанное с изменением хотя бы одного из ее термодинамических параметров, называется термодинамическим процессом.Если для данной системы внешние условия не изменяются и состояние системы с течением времени не меняется, то эта система находится в термодинамическом равновесии.

Моля́рная ма́сса вещества — отношение массы вещества к количеству молей этого вещества, то есть масса одного моля вещества. Для отдельных химических элементов молярной массой является масса одного моля отдельных атомов этого элемента. В этом случае молярная масса элемента, выраженная в г/моль, численно совпадает с массой атома элемента, выраженной в а.е.м. (атомная единица массы). Однако надо чётко представлять разницу между молярной массой и молекулярной массой, понимая, что они равны лишь численно и отличаются по размерности.

Молярные массы сложных молекул можно определить, суммируя молярные массы входящих в них элементов.

Например, молярная масса воды (H2O) есть MH2O = 2 MH +MO = 2·1+16 = 18 (г/моль).

Стоит отметить, что, например, молярная масса кислорода как элемента = 16 (г/моль), а вещества — (O2) = 32 (г/моль). В системе СИ единицей измерения является килограмм на моль (кг/моль). Обозначается буквой M.

Число́ Авога́дро, конста́нта Авогадро, постоянная Авогадро — физическая величина, численно равная количеству специфицированных структурных единиц (атомов, молекул, ионов, электронов или любых других частиц) в 1 моль вещества. Определяется как количество атомов в 12 граммах (точно) чистого изотопа углерода-12. Обозначается обычно как NA, реже как L.

Моль— количество вещества, которое содержит NA структурных элементов (то есть столько же, сколько атомов содержится в 12 г 12С), причём структурными элементами обычно являются атомы, молекулы, ионы и др. Масса 1 моля вещества (молярная масса), выраженная в граммах, численно равна его молекулярной массе, выраженной в атомных единицах массы. Например:

• 1 моль натрия имеет массу 22,9898 г и содержит примерно 6,02·1023 атомов

• 1 моль фторида кальция CaF2 имеет массу (40,08 + 2×18,998) = 78,076 г и содержит 6,02·1023 молекул

• 1 моль тетрахлорида углерода CCl4, масса которого равна (12,011 + 4×35,453) = 153,823 г

• и т. п.

На заре развития атомной теории (1811) А. Авогадро выдвинул гипотезу, согласно которой при одинаковых температуре и давлении в равных объёмах идеальных газов содержится одинаковое число молекул. Позже было показано, что эта гипотеза есть необходимое следствие кинетической теории, и сейчас она известна как закон Авогадро. Его можно сформулировать так: один моль любого газа при одинаковых температуре и давлении занимает один и тот же объем, при нормальных условиях равный 22,41383 л. Эта величина известна как молярный объем газа.

Термодинамическое равновесие — состояние системы, при котором остаются неизменными по времени макроскопические величины этой системы (температура, давление, объём, энтропия) в условиях изолированности от окружающей среды. В общем, эти величины не являются постоянными, они лишь флуктуируют (колеблются) возле своих средних значений. Если равновесной системе соответствует несколько состояний, в каждом из которых система может находиться неопределенно долго, то о системе говорят, что она находится в метастабильном равновесии. В состоянии равновесия в системе отсутствуют потоки материи или энергии, неравновесные потенциалы (или движущие силы), изменения количества присутствующих фаз. Отличают тепловое, механическое, радиационное (лучистое) и химическое равновесия. На практике условие изолированности означает, что процессы установления равновесия протекают гораздо быстрее, чем происходят изменения на границах системы (то есть изменения внешних по отношению к системе условий), и осуществляется обмен системы с окружением веществом и энергией. Иными словами, термодинамическое равновесие достигается, если скорость релаксационных процессов достаточно велика (как правило, это характерно для высокотемпературных процессов) либо велико время для достижения равновесия (этот случай имеет место в геологических процессах).

В реальных процессах часто реализуется неполное равновесие, однако степень этой неполноты может быть существенной и несущественной. При этом возможны три варианта:

1 равновесие достигается в какой-либо части (или частях) относительно большой по размерам системы — локальное равновесие,

2 неполное равновесие достигается вследствие разности скоростей релаксационных процессов, протекающих в системе — частичное равновесие,

3 имеют место как локальное, так и частичное равновесие.

В неравновесных системах происходят изменения потоков материи или энергии, или, например, фаз.

Квазистатический процесс в термодинамике — идеализированный процесс, состоящий из непрерывно следующих друг за другом состояний равновесия. Такие процессы называют также квазиравновесными, так как систему в каждый момент времени можно считать находящейся в состоянии термодинамического равновесия.

В термодинамике наиболее часто рассматриваются следующие виды квазистатических процессов:

• Изохорный процесс — процесс, происходящий при постоянном объёме;

• Изобарный процесс — процесс, происходящий при постоянном давлении;

• Изотермический процесс — процесс, в котором температура остается постоянной;

• Адиабатический процесс Пуассона — процесс, который совершается без подвода или отвода тепла, причем медленно. К примеру, адиабатическое расширение в вакууме не является квазистатическим процессом.

Равновесная термодинамика описывает системы, находящиеся в состоянии термодинамического равновесия. Любое изменение состояния системы выводит её из состояния равновесия, и в системе начинаются неравновесные переходные и релаксационные процессы, которые в общем случае очень сложны для описания. Однако многие процессы в технике с достаточной для практических целей точностью могут описываться как квазиравновесные.

Модель квазистатических процессов значительно упрощает анализ термодинамических систем. При описании текущего состояния системы, в которой происходит квазистатический процесс, требуется столько же параметров, сколько и для макроскопического описания равновесного состояния. Квазистатические процессы не реализуются в природе, но являются хорошей моделью для процессов, протекающих достаточно медленно по сравнению с процессами установления термодинамического равновесия в системе. Для квазистатического процесса скорость изменения макроскопического параметра должна удовлетворять условию , где — время релаксации, — характерный масштаб изменения величины .