Распределение молекул газа по скоростям и энергиям теплового движения. Опыт Штерна

При выводе основного уравнения молекулярно-кинетической теории полагалось, что молекулы имеют различные скорости. После многократных соударений скорость каждой молекулы изменяется по модулю и направлению. Но из-за хаотического движения молекул все направления движения равновероятны, т. е. в любом направлении в среднем движется равное число молекул.

Согласно молекулярно-кинетической теории, как бы ни изменялись при столкновениях скорости молекул, средняя квадратичная скорость молекул массой m₀ в газе, который находится в состоянии равновесия при Т= const, остается неизменно и равной

Это объясняется тем, что в газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем статистическое распределение молекул по скоростям, подчиняющаяся вполне определенному статистическому закону. Этот закон теоретически выведен Дж. Максвеллом.

При выводе закона распределения молекул по скоростям Максвелл сделал предположение, что газ состоит из огромного числа N тождественных молекул, которые находятся в состоянии беспорядочного теплового движения при одинаковой температуре. Также предполагалось, что силовые поля на газ не действуют.

Закон Максвелла описывается некоторой функцией f(ν), которая называется функцией распределения молекул по скоростям. Если разбить диапазон скоростей молекул на малые интервалы, которые равны dν, то на каждый интервал скорости приходится число молекул dN(ν), имеющих скорость, которая заключена в этом интервале. Функция f(ν) задает относительное число молекул dN(ν)/N, скорости которых находятся в интервале от ν до ν+dν, т. е.

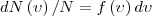откуда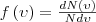
Применяя методы теории вероятностей, Максвелл получил функцию f(ν) — закон о распределеня молекул идеального газа по скоростям:

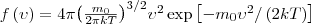
конкретный вид функции зависит от вида газа (от массы молекулы) и от параметра состояния (от температуры Т).

График функции (1) приведен на рис. 1. Так как при возрастании ν множитель exp[–m₀ν²/(2kT)] уменьшается быстрее, чем увеличивается множитель ν², то функция f(ν), начинаясь от нуля, достигает максимума при ν_B, и затем асимптотически стремится к нулю. Кривая несимметрична относительно ν_B.

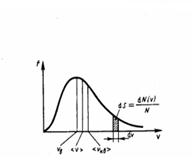
Рис.1

Относительное число молекул dN(ν)/N, со скоростями, лежащими в интервале от ν до ν+dν, рассчитывается как площадь заштрихованной полоски на рис. 1. Площадь, которая ограничена кривой распределения и осью абсцисс, равна единице. Это значит, что функция f(ν) удовлетворяет условию нормировки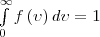

Скорость, при которой максимальна функция распределения молекул идеального газа по скоростям, называется наиболее вероятной скоростью, значение которой можно найти продифференцировав выражение (1) (постоянные множители опускаем) по аргументу ν, при этом приравняв результат нулю и используя условие для максимума выражения f(ν):

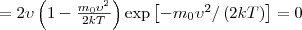
Значения ν=0 и ν=∞ соответствуют минимумам выражения (1), а значение ν, при котором выражение в скобках становится равным нулю, и есть искомая наиболее вероятная скорость ν_B: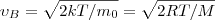

Из формулы (2) мы видим, что при возрастании температуры максимум функции распределения молекул по скоростям (рис. 2) движется вправо (при этом становится больше значение наиболее вероятной скорости). Однако площадь, которая ограничена кривой, не меняется, поэтому кривая распределения молекул по скоростям при повышении температуры будет растягиваться и понижаться.

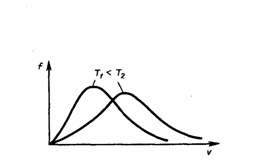
Рис.2

Средняя скорость молекулы <ν> (средняя арифметическая скорость) определяется по формуле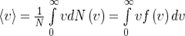
Подставляя сюда f(ν) и интегрируя, получаем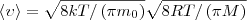
Скорости, которые характеризуют состояние газа: 1) наиболее вероятная 2) средняя 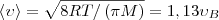3) средняя квадратичная 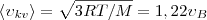(рис. 1). Исходя из распределения молекул по скоростям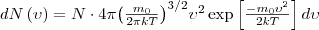

найдем распределение молекул газа по значениям кинетической энергии ε. С этой целью перейдем от переменной ν к переменной ε=m₀v²/2. Подставив в (4) 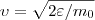и 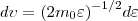, получим

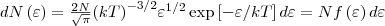где dN(ε) — число молекул, которые имели кинетическую энергию поступательного движения, заключенную в интервале от ε до ε + dε.

Значит, функция распределения молекул по энергиям теплового движения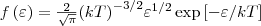

Средняя кинетическая энергия <ε> молекулы идеального газа

т. е. получили результат, совпадающий с формулой о средней кинетической энергии движения одной молекулы идеального газа, выводимой из молекулярно-кинетической теории.

Опыт Штерна.Первое опытное определение скоростей молекул провел Штерн в 1920 году. Прибор Штерна состоял из двух цилиндров разных радиусов, закрепленных на одной оси. Воздух из цилиндров был откачен до глубокого вакуума. Вдоль оси натягивалась платиновая нить, покрытая тонким слоем серебра. При пропускании по нити электрического тока она нагревалась до высокой температуры (~1200^оС), что приводило к испарению атомов серебра.

В стенке внутреннего цилиндра была сделана узкая продольная щель, через которую проходили движущиеся атомы серебра. Осаждаясь на внутренней поверхности внешнего цилиндра, они образовывали хорошо наблюдаемую тонкую полоску прямо напротив прорези.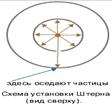

Цилиндры начинали вращать с постоянной угловой скоростью ω. Теперь атомы, прошедшие сквозь прорезь, оседали уже не прямо напротив щели, а смещались на некоторое расстояние, так как за время их полета внешний цилиндр успевал повернуться на некоторый угол. При вращении цилиндров с постоянной скоростью, положение полоски, образованной атомами на внешнем цилиндре, смещалось на некоторое расстояние l.

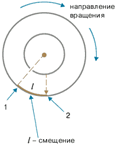
В точке 1 оседают частицы, когда установка неподвижна, при вращении установки частицы оседают в точке 2.

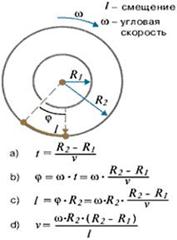
Полученные значения скоростей подтвердили теорию Максвелла. Однако о характере распределения молекул по скоростям этот метод давал приблизительные сведения.

Более точно распределение Максвелла было проверено опытами Ламмерта, Истэрмана, Элдриджа и Коста. Эти опыты достаточно точно подтвердили теорию Максвелла.

Прямые измерения скорости атомов ртути в пучке были выполнены в 1929 году Ламмертом. Упрощенная схема этого эксперимента показана на рис. 3.

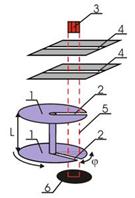
Рис.3. Схема опыта Ламмерта
1 - быстро вращающиеся диски, 2 - узкие щели, 3 - печь, 4 - коллиматор, 5 - траектория молекул, 6 – детектор

Два диска 1, насаженные на общую ось, имели радиальные прорези 2, сдвинутые друг относительно друга на уголφ. Напротив щелей находилась печь 3, в которой нагревался до высокой температуры легкоплавкий металл. Разогретые атомы металла, в данном случае ртути, вылетали из печи и с помощью коллиматора 4 направлялись в необходимом направлении. Наличие двух щелей в коллиматоре обеспечивало движение частиц между дисками по прямолинейной траектории 5. Далее атомы, прошедшие прорези в дисках, регистрировались с помощью детектора 6. Вся описанная установка помещалась в глубокий вакуум.

При вращении дисков с постоянной угловой скоростью ω, через их прорези беспрепятственно проходили только атомы, имевшие некоторую скорость υ. Для атомов, проходящих обе щели должно выполняться равенство:

где Δt₁ - время пролета молекул между дисками, Δt₂ - время поворота дисков на угол φ. Тогда: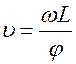

Изменяя угловую скорость вращения дисков можно было выделять из пучка молекулы, имеющие определенную скорость υ, и по регистрируемой детектором интенсивности судить об относительном содержании их в пучке.

Таким способом удалось экспериментально проверить Максвелловский закон распределения молекул по скоростям.