
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Закон распределения Пуассона.
Определение: Дискретная случайная величина Х имеет закон распределения Пуассона с параметром 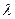 =np>0 , если она принимает значения 0,1,2,3,….,m,….(Бесконечное, но счетное множество значений) с вероятностями
=np>0 , если она принимает значения 0,1,2,3,….,m,….(Бесконечное, но счетное множество значений) с вероятностями
 . (4)
. (4)
Ряд распределения Пуассона имеет вид:
| Хi | … | m | … | |||
| pi | 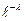
| 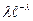
| 
| … | 
| … |
Определение закона Пуассона корректно, так как основное свойство ряда распределения  выполнено, так как
выполнено, так как 
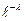 +
+ 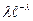 +
+  +….+
+….+  +…=
+…=
= 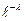

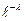
 =1 (ибо в скобках записано разложение в ряд функции
=1 (ибо в скобках записано разложение в ряд функции 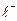 при х=
при х= 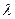 ).
).
Составим многоугольники распределений для случайной величины Х с параметрами распределения 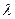 =0,5 ;
=0,5 ; 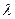 =1;
=1; 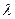 =2;
=2; 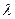 =3,5. Для этого составим вспомогательную таблицу:
=3,5. Для этого составим вспомогательную таблицу:
m/ 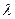
| 0,5 | 3,5 | ||
| 0,608581 | 0,37037 | 0,137174 | 0,030919 | |
| 0,30429 | 0,37037 | 0,274348 | 0,108217 | |
| 0,076073 | 0,185185 | 0,274348 | 0,189379 | |
| 0,012679 | 0,061728 | 0,182899 | 0,220943 | |
| 0,001585 | 0,015432 | 0,091449 | 0,193325 | |
| 0,000158 | 0,003086 | 0,03658 | 0,135327 |

Теорема: Математическое ожидание и дисперсия случайной величины Х, распределенной по закону Пуассона совпадают и равны параметру 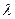 этого закона
этого закона
М(Х)= 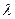 , (5)
, (5)
D(X)= 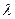 . (6).
. (6).
Доказательство:
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.
По определению, когда дискретная случайная величина принимает счетное множество значений:

Первый член суммы (соответствующий m=0) равен нулю, следовательно, суммирование можно начинать с m=1:

Таким образом, параметр 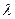 а представляет собой не что иное, как математическое ожидание случайной величины Х.
а представляет собой не что иное, как математическое ожидание случайной величины Х.
Дисперсией случайной величины Х называют математической ожидание квадрата отклонения случайной величины от ее математического ожидания:

Однако, удобнее ее вычислять по формуле:
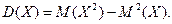
Поэтому найдем сначала
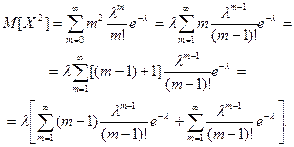
По ранее доказанному

кроме того,

следовательно,

Далее можно найти дисперсию случайной величины Х:
 .
.
Таким образом, дисперсия случайной величины, распределенной по закону Пуассона, равна ее математическому ожиданию 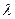 .▄
.▄
Это свойство распределения Пуассона часто применяют на практике для решения вопроса, правдоподобна ли гипотеза о том, что случайная величина распределена по закону Пуассона. Для этого определяют из опыта статистические характеристики - математическое ожидание и дисперсию - случайной величины. Если их значения близки, то это может служить доводом в пользу гипотезы о пуассоновском распределении; резкое различие этих характеристик, напротив, свидетельствует против подобной гипотезы.
Вообще говоря, закон Пуассона является предельным для биномиального распределения.
Так как функция вероятностей Пуассона хорошо аппроксимирует функцию вероятностей, определяемую по формуле Бернулли при  . Так как при этом вероятность р события А в каждом испытании мала, то закон распределенипя Пуассона называется часто законом редких явлений.
. Так как при этом вероятность р события А в каждом испытании мала, то закон распределенипя Пуассона называется часто законом редких явлений.
По закону Пуассона распределены, например, число отказов сложной системы в «нормальном режиме», число требований на обслуживание, поступивших на единицу времени в системах массового обслуживания, число рождения пятерней, число событий, попадающих на произвольный отрезок времени для простейшего потока событий.
Дата добавления: 2015-01-18; просмотров: 325; Мы поможем в написании вашей работы!; Нарушение авторских прав |