Свойства функции распределения вероятностей случайной величины

1.Значения функции распределения вероятностей принадлежат отрезку :
.
2.Функция распределения вероятностей – неубывающая функция, то есть:
, если .
Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале , равна приращению функции распределения вероятностей на этом интервале:
.
Следствие 2. Вероятность того, что непрерывная случайная величина примет одно определенное значение, равна нулю.
Используя последнее следствие, легко убедиться в справедливости следующих равенств:
.
3.Если возможные значения непрерывной случайной величины принадлежат интервалу , то:
, если ;
, если .
Следствие.Если возможные значения непрерывной случайной величины расположены на всей числовой оси, то справедливы следующие предельные соотношения:
;
.
Плотностью распределения вероятностей непрерывной случайной величины 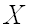называют функцию – первую производную от функции распределения вероятностей :
.
Таким образом, функция распределения вероятностей является первообразной для плотности распределения вероятностей.
Теорема. Вероятность того, что непрерывная случайная величина 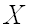примет значение, принадлежащее интервалу , равна определенному интегралу от плотности распределения, взятому в соответствующих пределах:
.
Следовательно, зная плотность распределения вероятности , можно найти функцию распределения по формуле
.