Билет №1. Дискретная случайная величина, закон и функция распределения

Дискретной называют случайную величину, значения которой изменяются не плавно, а скачками, т.е. могут принимать только некоторые заранее определённые значения. Например, денежный выигрыш в какой-нибудь лотерее, или количество очков при бросании игральной кости, или число появления события при нескольких испытаниях. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (счётным множеством)
Для сравнения - непрерывная случайная величина может принимать любые значения из некоторого числового промежутка: например, температура воздуха в определённый день, вес ребёнка в каком-либо возрасте, и т.д.

Закон распределения дискретной случайной величины представляет собой перечень всех её возможных значений и соответствующих вероятностей. Сумма всех вероятностей Σp_i = 1. Закон распределения также может быть задан аналитически (формулой) и графически (многоугольником распределения, соединяющим точки (x_i; p_i)

Функция распределения случайной величины - это вероятность того, что случайная величина (назовём её ξ) примет значение меньшее, чем конкретное числовое значение x:
F(X) = P(ξ < X).
Для дискретной случайной величины функция распределения вычисляется для каждого значения как сумма вероятностей, соответствующих всем предшествующим значениям случайной величины. Ниже будет приведён пример, разъясняющий смысл сказанного.

Закон распределения дискретной случайной величины можно изобразить графически. С этой целью на прямоугольной системе координат строят точки M1(x1; p1),M2(x2; p2), …, Mn(xn; pn), где xi – возможные значения случайной величины, а pi – соответствующие вероятности, и соединяют их последовательно отрезками прямых. Полученную фигуру называют многоугольником распределения. Построим многоугольник распределения дискретной случайной величины X, заданной следующим законом распределения:

Математическое ожидание: .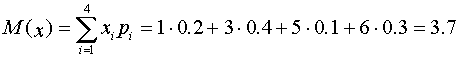

Дисперсия: .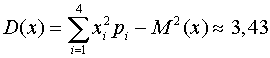

Среднее квадратическое отклонение: .