Числовые характеристики непрерывных случайных величин

Математическим ожиданием непрерывной случайной величины 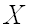, возможные значения которой принадлежат отрезку 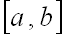, называют определенный интеграл
.
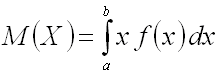Если возможные значения принадлежат всей числовой оси, то

(предполагается, что несобственный интеграл, стоящий в правой части равенства, существует).
Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.
Если возможные непрерывной случайной величины 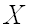принадлежат отрезку 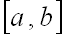, то
.
Если возможные значения принадлежат всей числовой оси, то

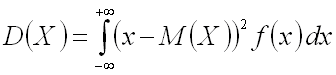
(предполагается, что несобственный интеграл, стоящий в правой части равенства, существует).
Средним квадратическим отклонением непрерывной случайной величины называют, как и для величины дискретной, квадратный корень из дисперсии:
.

4. Среднее квадратическое отклонение. Мода, медиана, моменты, асимметрия и эксцесс, квантили. Производящие функции.

Среднее квадратическое отклонение дискретной случайной величины, оно же стандартное отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии:
σ(X) = √D(X)

Мода дискретной случайной величины Mo(X) - это значение случайной величины, имеющее наибольшую вероятность. На многоугольнике распределения мода - это абсцисса самой высокой точки. Бывает, что распределение имеет не одну моду.

Мода — это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является варианта, обладающая наибольшей частотой. При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле:

где:

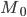§ — значение моды

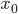§ — нижняя граница модального интервала

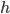§ — величина интервала

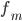§ — частота модального интервала

§ — частота интервала, предшествующего модальному

§ — частота интервала, следующего за модальным

Медиана —это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части.

Для определения медианы в дискретном ряду при наличии частот сначала вычисляют полусумму частот , а затем определяют, какое значение варианта приходится на нее. (Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле:

М_е = (n_{(число признаков в совокупности)} + 1)/2,

в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда).

При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:

где:

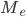§ — искомая медиана

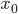§ — нижняя граница интервала, который содержит медиану

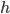§ — величина интервала

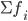§ — сумма частот или число членов ряда

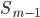§ - сумма накопленных частот интервалов, предшествующих медианному

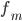§ — частота медианного интервала